Basamak Kavramı Soruları

Lise Matematik
Basamak KavramıÖrnek 20:
x=m-2
y= m2 + 4m + 1
parametrik denklemleri ile lanımlı y=f(x) fonksiyonu veriliyor.
Buna göre, f(x - 3) + 4 fonksiyonunun simetri ekseninin
yatay ekseni kestiği noktanın apsisi ile fonksiyonun dü-
şey ekseni kestiği noktanın ordinatinin toplamı kaçtır?
A)
B) 1
C) 2
D)3
E) 4

Lise Matematik
Basamak Kavramı1.
5AB ve 4AB üç basamaklı doğal sayılardır.
2
A-B = 3
olduğuna göre, 5AB - 4AB farkı kaçtır?
500+10At B- 4ooHoA & B
- 100
2. ab iki basamaklı bir doğal sayıdır.
ab = x
olduğuna göre, ab5 sayının x cinsinden eşiti nedir?
3. ab4 üç basamaklı bir doğal sayıdır.
ab4 = x
olduğuna göre, ab45 sayının x cinsinden eşiti nedir?
a
a bhew
100 lob +
ipbevou

Lise Matematik
Basamak Kavramı93
39
S
1 85 tir.
büyüğü en az kaç-
15. AB ve BA iki basamaklı doğal sayılardır.
A²-B2 = AB - BA
olduğuna göre, kaç tane AB sayısı yazılabilir?
A) 19
B) 18 C) 17
D) 16 E) 15
=10A+B-103-A
ab iki b:
3
D) 18
E) 19
A?
x.at
xb=
olduğ
tır?
A = 9A-9B
(9|A-B)
A) 11

Lise Matematik
Basamak Kavramı6. GUN
Çözüm
için
izle
55798
Bölünebilme
1.
n kenarlı bir çokgen içine A pozitif tam sayısı yazılıyor.
Bu sembol
A
A
-
n
olarak tanımlanıyor.
AB iki basamaklı bir doğal sayı olmak üzere,
ve
AB
AB
ifadelerinin sonuçları tam sayıdır.
Buna göre, bu şartı sağlayan kaç tane AB sayısı
vardır?
A) 4 B) 5
C) 6 D) 7 E) 8

Lise Matematik
Basamak Kavramıod
1.
2
AB iki basamaklı bir doğal sayı, C doğal sayıdır.
A + B = 2
A 20
şartını sağlayan AB sayılarına "İKİLİK SAYI" denir.
Buna göre, kaç farklı "İKİLİK SAYI" vardır?
A) 15
B) 16
C) 18
E) 20
D) 19
1.
2
22 23 24 25 26
20
![8.
ab ve ba iki basamaklı doğal sayılardır.
(ab) km/sa
= (ba) km/sa
K
M
Asfalt yol
Toprak yol
3
K noktasından aracı ile hareket edip M noktasına giden
Emir, [KL] asfalt yolu ile [LM] toprak yolunu kullanıyor.
Asfalt yolda (ba) km/sa hızla a saat, toprak yolda (ab)
km/sa hızla b saat hareket ediyor.
Toprak yolun uzunluğu, asfalt yolun uzunluğundan
33 km fazla olduğuna göre [KL] yolu kaç kilometredir?
A) 296
B) 415
C) 425
D) 458
E) 463](https://media.kunduz.com/media/question/raw/20211223090010398056-1152508.jpg?w=256)
Lise Matematik
Basamak Kavramı8.
ab ve ba iki basamaklı doğal sayılardır.
(ab) km/sa
= (ba) km/sa
K
M
Asfalt yol
Toprak yol
3
K noktasından aracı ile hareket edip M noktasına giden
Emir, [KL] asfalt yolu ile [LM] toprak yolunu kullanıyor.
Asfalt yolda (ba) km/sa hızla a saat, toprak yolda (ab)
km/sa hızla b saat hareket ediyor.
Toprak yolun uzunluğu, asfalt yolun uzunluğundan
33 km fazla olduğuna göre [KL] yolu kaç kilometredir?
A) 296
B) 415
C) 425
D) 458
E) 463
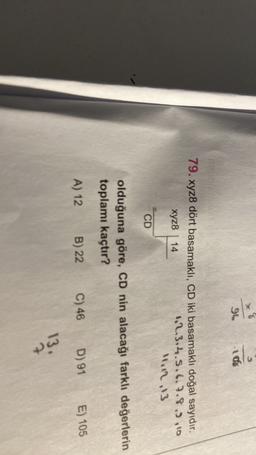
Lise Matematik
Basamak Kavramı8.
alu
96
79. xyz8 dört basamaklı, CD iki basamaklı doğal sayıdır.
xyz8 | 14
1.2.3.4.5.6.7.8,3,10
linn,13
CD
olduğuna göre, CD nin alacağı farklı değerlerin
toplamı kaçtır?
A) 12
B) 22
C) 46
D) 91
E) 105
13.

Lise Matematik
Basamak KavramıÖSYM TARZI ORİJİNAL
Basamak Kavrc
3.
Test - 4
1.
CBA
do 265 6.5t
ACB
BAC
ABC
0
673
ba
b
BCA
756
ACB
c
639
Şekilde bir mahallenin sokak krokisi verilmiştir. İki sokağın
kesişim yerlerine kavşaklar yerleştirip o kavşağın adı sokak
numaralarının toplamı olarak isimlendirilmiştir.
Örneğin, X kavşağının adı ABC + CBA olarak verilmiştir.
Her sokağın numarası üç basamaklı sayilardan oluş-
tuğuna göre, yukarıdaki krokide kavşakların adlarını
oluşturan sayıların toplamı aşağıdakilerden hangisi
olamaz?
ORIJINAL YAYINLARI
609A +3 335 +2696
D) 3330
E) 3996
C) 2664
B) 1998
A) 1332

Lise Matematik
Basamak KavramıOO
CARI
TEST - 8
Bu testi süre tutmadan, sadece soru tipinin mantığını anlayarak de
3. ABC üç be
verilmişt
1.
ACB ve AC sırasıyla üç ve iki basamaklı sayılardır.
ACB
AC
So
+
4BC
işlemine göre, A.C çarpımı kaçtır?
21
321
C) 28
D) 24
B) 27
old
A) 30
A
Tri bir odanın

Lise Matematik
Basamak Kavramı9. abc üç basamaklı sayısı:
1. b silinirse ac iki basamaklı sayısının 11 kati,
II. c silinirse ab iki basamaklı sayısının 10 katı
oluyor.
Buna göre, yukarıdaki koşulları sağlayan her abc sayi-
si, rakamları toplamının kaç katıdır?
A) 50
B) 55
C) 60
D) 90
E) 99

Lise Matematik
Basamak KavramıX=
t 6. xyz ve zyx üç basamaklı sayılardır.
y =
XyZ = zyx + 396
koşuluna uyan kaç tane xyz sayısı vardır?
Yuki
birle
değ
sayı
A) 43
B) 47
Bur
Co
C) 50 D) 52 E) 55
100x + 109+2 = 100€ + 1097
99x992
99.(x-2)=396
x - 2 =
X=
y =
Yayincik
old

Lise Matematik
Basamak KavramıA
TYT / TEMEL MATEMATİK
11. xyz, yxz ve zxy üç basamaklı doğal sayılar olmak üzere,
Ayşe hemşire kızı Zeynep'in 4 ayda bir kilosunu tartıp so-
nucunu bebek odasındaki panoya bebeğinin resminin altı-
na kaydediyor.
12.
Zeynep 4 aylık
Zeynep 8 aylık
Zeynep 12 aylık
xyz birim
yxz birim
zxy birim
-270
x
x+396
Zeynep'in 8 aylıkken kilosu 4 aylıkken kilosundan 270 birim
fazla, 12 aylıkken kilosundan 396 birim azdır.
Buna göre, x-(y + 2) ifadesinin eşiti aşağıdakilerden han-
gisi olabilir?
A) 40
B) 32
C) 28
D) 7
E) O
xy Z+270=4XZ
Ox+10y +2 +270=100y+lox+2

Lise Matematik
Basamak Kavramı4./1 den itibaren pozitif tek sayılar kendi adedi kadar
yan yana yazılarak 139 basamaklı bir T sayısı
oluşturuluyor.
T= 133355555
Buna göre, bu sayının son üç basamağı aşağı-
dakilerden hangisidir?
A) 171
B) 151
C) 919 D) 719
E) 191

Lise Matematik
Basamak KavramıIki basam ki aa ve bb sayıları için,
(aa)2 + (bb)2 = 1573
eşitliği veriliyor.
Buna göre a + b toplamı kaçtır?
A3
B) 4
C) 5
D) 6
E) 7
(10)
12102t 121.6? = 1573
azteo ?= 13
o
2+3=5
12.
1 den 54 e kadar olan tam sayılar soldan sağa doğru
yan yana yazılıyor.
K = 123456 ... 525354
biçiminde 99 basamakl bir K sayısı oluşuyor.
Buna göre K nin soldan 60. rakamı kaçtır?
AO
B) 1
C) 2
D) 3
E) 4.
? (21 lugler, 15, 16, 17, 18 a 20
21 22 23 24 25 26 2t 28 29 30
a
TYT Matematik
1
Y 82
82 53
84

Lise Matematik
Basamak Kavramıa-
28.
AB
CD
E
E
1
3
4
5
2
7
6
8
00
9
1
0
1
1
1
2
N
1
3
1
4
1
5
Yukarıdaki şekilde A sütunundan başlayarak sırasıyla
her bir sütunda bir rakam olacak şekilde 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ... sayılarının rakamla-
ri yazılıyor.
gek
Buna göre 2019 sayısını yazarken hangi sütun kul-
lanılmamıştır?
A) E B) D C) C D) B E) A

Lise Matematik
Basamak Kavramı12. Rakamlarından biri 5 olan üç basamaklı bir doğal sayi-
nin diğer iki rakamı aynıdır. Bu sayının yüzler ve birler
basamağı yer değiştirdiğinde sayının değeri 198 azal-
maktadır.
Buna göre, bu sayının alabileceği değerlerin topla-
mi kaçtır?
A) 1080 B) 1130
A AA5-198
C) 1206
D) 1308
E) 1405
