Köklü Sayılar Soruları

9. f: R → R, f(x) = -x3 + 6x2 + ax = fonksiyonunun R de azalan bir fonksiyon olma- si için, a nin bulunduğu en geniş aralık aşağıda- kilerden hangisi olmalıdır? nirao A) (0, -10] B) (0, -12] C) (0, -2] D) [0, 12] E) (-12, -2]

MATEMATİK 5. Aşağıda sadece ön yüzlerinde birer kareköklü ifadenin yazılı olduğu dört kart gösterilmiştir. 23 JDON 40 71 Bu kartlann kullanıldığı bir oyunda kartların puan değeri şöyle hesaplanmaktadır: • Kartın üzerindeki kareköklü ifadenin en yakın olduğu doğal sayı değeri kartın puanını vermektedir. Buna göre verilen kartlara sahip bir oyuncunun kazanacağı toplam puan kaçtır? A) 21 B) 23 C) 25 D) 27

D KONU KAVRAMA TESTİ 30 a 5. Eşit kapasiteli 4 işçi birlikte işe başlıyor ve her saat so- nunda bir işçi işten ayrılıyor. Son işçi kaldığında çalışmaya devam ederek işi tamamlıyor. İşin tamamı 8 saatte tamamlandığına göre, bir işçi bu işin tamamini kaç saatte tamamlar? A) 10 B) 11 C) 12 D) 13 E) 14 1 Lb UV 6. Bir işi Damla 15 saatte, Ozan 12 saatte yapabilmektedir. Ozan işe başladıktan 6 saat sonra Damla işe başlıyor ve beraber işi bitiriyorlar. bon Buna göre, işin tamamı kaç saatte bitmiştir? 35 sv 32

20) Bir aracın ön ve arka amortisör uzunlukları ve aracın yaptığı km ye göre amortisörlerin aşınma miktarlarl aşa- ğıdaki tabloda verilmiştir. Uzunluk (cm) Aşınma Miktarı (1000 km de) Ön 514+ 12 ✓ 3 cm Amortisör Arka ✓2 cm 573+78 Amortisör Buna göre, kaç km sonra aracın ön ve arka amorti- sörlerin uzunlukları eşit olur? A) 7000 B) 6000 C) 5000 E) 3000

izve 8. Vx-3+37-x toplamının değeri reel sayılar kümesinde bulunabildiğine göre x nin hangi aralıkta olduğunu bulunuz. değeri 9.)7-473 ifadesinin hangi sayıyla çarpıldığında 1 olduğunu bulunuz. 10.7x-3)**2 = 1 denklemini sağlayan x değerlerinin toplamını bulunuz. X2 = Ç) Aşağıdaki çoktan seçmeli soruları okuyunuz ve soruların doğru seçeneğini işaretleyiniz,

8. A B Ć ir A noktasında bulunan Ali, en fazla 8 eşit adım ata- rak B noktasına ulaşıyor. Ali'nin bir adım uzunluğu 174 cm olduğuna göre, A ile B arasındaki uzaklık aşağıdakilerden hangi- si olamaz? u A) 61 cm B) 64 cm C) 67 cm D) 68 cm E) 73 cm

Buna göre, bu örüntüde kaç tane düzgün altıgen vardır? 11 A) 5 B) 6 C) 7 D) 8 E) 9 az 3652 6-22 J18 = 352 AYDIN YAYINLARI VTV3 3. Bir cetvelin başlangıç noktasına, uzunluğu bilinen bir çubuk Şekil 1 deki gibi yerleştirilmiştir. of th=7 00 Jambi A STAR 2 3 4 5 6 7 8 Şekil 1 V3 N 32 U3+57 25 . 2 5 6 8 Şekil 2 Daha sonra bu çubuk alttan itibaren 13 cm sinden Şekil 2 deki gibi kırılmıştır. Çubuğun cetvele dik olan kısmının uzun- luğu 73 cm olup, diğer ucu cetvelin 2 cm sine denk gelecek şekilde düşmüştür. Buna göre, bu çubuğun kırılmadan önceki boyu aşağı- daki tam sayılardan hangisine en yakındır? A) 2 B) 3 C) 4 D) 5 E) 6

3. = AV12 A 213 3/2 a A= BV18 2.3.5=30 E • = C/125 515 2 1 ve sembolleri Yukarıda verilen eşitliklerde , birer doğal sayıdır. 1 1 Buna göre, A.B.C çarpımı aşağıdakilerden han- gisi olabilir? 1 A) V15 B) V30 C) 732 C) 32 D) V40 E) V60 1 1 1 A√3 1 B-2 A.B.C = V3.2.5 = 30 - 2 1 1 C-15 (Yanıt B)

1252 450 352 20 5. Yarıçapının uzunluğu r olan bir dairenin çevresi 2nr'dir. 530 500 450 400 350 300 250 200 150 A 652 0 6282 1252 193 100 50 12/2 B A . Yukarıdaki şekilde verilen iki dairenin konumları ile ilgili bilgiler aşağıdaki gibi verilmiştir: Ipin uç noktaları olan A ve B noktalarına 0, ve 0, merkezli dairelere değecek şekilde yerleştirilmişti. Yarıçapları 212 cm ve v2 cm olan daireler, şekilde verilen ok yönlerinde döndürülerek C konumune getiriliyor, 0, merkezli daire 2 tam tur, 0, merkezli daire 1,5 turdan çok, 2 turdan az dönüyor. Yukarıdaki bilgilere göre, A ve B noktaları arasındaki ipin uzunluğu kaç santimetre olabilir? (n = 3 aliniz.) . Yukarıda termekte Bu veril renim d verilmis 1,5) 1,7 D) 65 B) 45 2 C) 55 A) 40 A) 6,396 2

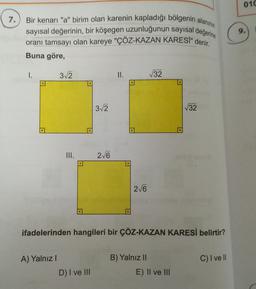
010 7. 9. Bir kenarı "a" birim olan karenin kapladığı bölgenin alanının sayısal değerinin, bir köşegen uzunluğunun sayısal değerine oranı tamsayı olan kareye "ÇÖZ-KAZAN KARESİ" denir Buna göre, 32 II. 132 3/2 132 . III. 216 . 216 ifadelerinden hangileri bir ÇÖZ-KAZAN KARESI belirtir? C) I ve II A) Yalnız! D) I ve III B) Yalnız II E) II ve III

6. a, b, c, d birer gerçek sayı a > 0, c# 0, b 2 0 ve d > 0 olmak üzere Va2.b = ab. ab icb = (a c)b, b abcd = a.cb.d ve 'dir. √d C d Aşağıda belirli uzunlukta bir koli bandı verilmiştir. ab a 1200 m Bu bant aşağıdaki tabloda verilen uzunlukta parçalara ayrılacaktır. Tablo: kesilecek Parçaların Uzunlukları Parçalar Uzunluğu (m) K V3 L 513 M 23 Hüseyin Bey yukarıdaki koli bandından birer tane K, L ve M parçaları kesip bu parçaları bir koliye yapıştırıyor. Daha sonra koli bandının kalan kısmından; tabloda verilen uzunlukların dışına çıkmadan her parçadan en az bir tane elde edecek şekilde parçalar kesiyor. Buna göre Hüseyin Bey'in, bantın tamamını kullanarak kestiği parçaların toplam sayısı en az kaçtır? A) 6 B) 7 C) 8 D) 9 8. SINIF / LGS 3 4

ADAY TEMEL M 5. 2 sayısının yaklaşık değerini hesaplamak isteyen Aysel, hesap makinesi kullanarak aşağıdaki verileri not etmiştir: • 142 = 196 • 152 = 225 1412 = 19881 1422 = 20164 14142 = 1999396 14152 = 2002225 • 141422 = 199996164 141432 = 200024449 . Bu not kâğıdına göre, Aysel V2 sayısının yaklaşık değerini ondalık şekilde yazmak isterse, virgülden sonraki ilk kaç rakamı doğru biçimde yazabilir? A) 1 B) 2 C) 3 D) 4 E) 5

1 13 88 7 7683 Yukarıdaki dinozorun kuyruk uzunluğu 432 m, ön ayakları ile kuyruğu arasındaki mesafesi (768 m'dir. Dinozor kendisini savunmak için ön ayakları etrafında dairesel dönüş yapabilmektedir. Buna göre kuyruğunun üzerine kalkabi- len bu dinozorun savunma bölgesinin alanı kaç m2 dir? (T = 3 alınız.) A) 7056 B) 2304 C) 1296 M. 8.1.3.5 D) 1194 2 tr Q] II

öd Yançapın uzunluğu r olan bir çemberin çevresi 2'dir. Bir tekerlek 1 tam tur döndüğünde çevresi kadar yol gider. a ve b pozitif sayılar olmak üzere, y a'b = ay /a²b ab dir. Efe'nin bisikletinin tekerleğinin yarıçapı 30 cm'dir. Efe evinden markete, parka ve okula bisikleti ile gitmiştir. A a, 5012 - A 50=5Jz 25 swa orog 160=2515 SE 55 30 cm 3Toplam 110.) 3e Efe bisikleti ile markete giderken bisikletinin tekerleği 50 tam tur dönmüştür. Efe bisikletle packa giderken bisikletinin tekerleği 60 tam tur dönmüştür. Efe bisikleti ile okula giderken bisikletinin tekerleğinin attığı tur sayısı markete giderken attığı tur sayısından fazla, par E derken attiğfur sayısından azdır. Buna göre, Efe'nin eville okulu arasındaki uzaklık metre cinsinden aşağıdakilerden hangisi olabilir? (n = 3 alınız.) (t B) C) 40/5 D A) 50/3 coton 50.87150 3= tendon

16. Aşağıdaki eni 8 br, boyu 10/10 br olan dikdörtgen levha, eninden 10,25 br’lik, boyundan 10,4 br’lik aralıklarla dikdörtgen parçalara ayrılıyor. ✓0,4 0,4 ✓0,25 0,25 8 br 10/10 br Buna göre, elde edilecek toplam parça sayısı kaç tane olur? plene D) 800 C) 1200 E) 900 A) 720 B) 600

un 27. Aşağıda, köşe noktaları Az. Ag, Ag, Ay ve Aş olan düzgün beşgen gösterilmiştir. a- he AA .Az k . A, A2 Bu beşgenin köşeleri üzerinde işlemi her A köşesi için AA=A farklı A ve B köşeleri için AB, A ve B noktalarını bir- leştiren doğru parçasının orta dikmesi üzerinde bulu- nan köşe noktası biçiminde tanımlanıyor. (A, ⓇA3)®X=A5 olduğuna göre, X köşesi aşağıdakiler- den hangisidir? A) A, B) Az C) A3 D) A4 E) A5 (2015/YGS) :ëis Yayınlar