Kombinasyon Soruları

7. Bir öğrenci A, B, C, D, E, F ve G seçmeli derslerinden 3 tanesini seçecektir. C, D ve E dersleri aynı saatte verildiğine göre, bu öğ- renci kaç farklı ders seçimi yapabilir? A) 16 B) 18 C) 20 P) 22 E) 24 A B C D E (?)+(!)(3) 4 +6.3=22 6 8.

21. Bir torbada 1'den 9'a kadar numaralı birbirine eş dokuz tane kart vardır. Bu torbadan rastgele çekilen iki kartın üzerindeki sa- yıların toplamının 10 olması olasılığı kaçtır? A C D) 11 A) 1 B) 3 C) 1 1 3 cito D E) 1 / 3 9

5. A ile B kentlerini birbirine bağlayan yollar aşağıdaki gibi gösterilmiştir. 8. B 3 3.29 2 A Buna göre A kentinden B kentine en kısa yoldan kaç farklı biçimde gidilebilir? A) 126 B) 124 C) 120 D) 63 E) 61

18. Aynur ve Semih'in de aralarında bulunduğu 4 kız, 3 erkekten oluşan 7 kişilik bir gruptan üç kişilik bir ekip seçilmek isteniyor. • Aynur bu ekibe seçilirse Semih'in ekipte olma- ması gerekir. Semih bu ekibe seçilirse ekipte sadece 1 tane kızın olması gereklidir. Yukarıdaki şartları sağlayan üç kişilik kaç farklı ekip seçilebilir? A) 10 B) 12 C) 14 D) 15 E) 16

11. 6 kişilik gruptakilerin her biri yüzme, okçuluk, masa tenisi ve voleybol spor dallarından en az birini oynamaktadır. Buna göre 6 kişinin oynadıkları spor dallarına göre dağılımı kaç farklı biçimde olabilir? A) 216 B) 156 C) 64 D) 46 E) 30

2. A ve B rakamlarından oluşan boştan farklı birer küme olmak üzere, AB= A n {0, 2, 4, 6, 8} eşitliği sağlanıyorsa A kümesine B kümesinin orta kesişim kümesi denir. A kümesi, B = {0, 1, 2, 3, 4) kümesinin orta kesişim kümesi olduğuna göre, kaç farklı A kümesi vardır? A) 3 B) 7 C) 15 D) 31 E) 63

4. 6. h Bir satranç turnuvasına katılan 28 kişi, A ve R olmak üzere iki grup oluşturarak yarışmışlardır . Bu yarışı mayla ilgili aşağıdakiler bilinmektedir. Her oyuncu grubundaki diğer oyuncularla bir kez karşılaşmıştır. 11 Turnuva sonunda A grubundaki maç sayısı B grubundaki maç sayısından 108 azdır. Bu turnuvada galibiyete 2, beraberliğe 1 ve mağ- lubiyete 0 puan verilmiştir. 0 Buna göre, A grubunda yarışan ve 13 puan alan bir oyuncu en az kaç galibiyet elde etmiş olabilir? A) 4 B) 5 C) 6 D) 7 E) 8

BAKANLIO T.C.MILLI EGITIM Kazanım Kavrama Testi 13 7. 9 110 Sayma A, B, C birer rakam olmak üzere 1 << <B<A<9 10. koşulunu sağlayan kaç tane üç basamaklı ABC çift sayısı yazılabilir? (%) + (%) +(%) +45 + işleminin sonucu kaçtır? 2 B) A) 1087 E) 24 A) 16 B) 18 C) 20 D) 22 D) 1323 2/3145 bits 4/5, 6, 2,8 6/718

RULAR 12 Yukarıda 12 dairelik bir apartmanin posta kutuları verilmiş- tir. Bir halı yıkama şirketi bu posta kutularından 5 tanesine reklam amaçlı broşür bırakacaktır. Broşür bırakılan iki posta kutusu arasında en az bir posta kutusunun boş kalması koşulu ile bu işlem kaç farklı şekilde yapılabilir? B) 42 D) 56 E) 64 C) 48 A) 36 f sor oo Oooooooo

11. A = {1, 2, 3, 4, 5, 6, 10} { kümesinin 3 elemanlı alt kümelerinden biri seçiliyor. Seçilen bu kümenin elemanları çarpımının 5'in katı olduğu bilindiğine göre, bu kümede 3 rakamının bu- lunma olasılığı kaçtır? 5 A) B) D) 12 9 7 C) 8 5 3alng b 20 1 16 L 20 1 10 1 ŏ 10 9 56

E) 135 2. 6. 0233 YUV 24 10 in bir alt + Şekil özdeş 30 birim kareden oluşmuştur. Buna göre, şekildeki dikdörtgenlerden kaç ta- nesi taralı karelerin en az bir parçasını kapsar? B) 154 B) C) 150 D) 80 E) 60 Alemania A) 160 28 — £ 1 E) 27

1. 12. Bir internet sitesi için şifre almak isteyen Bayram'ın sitede karşılaştığı şifre koşulları aşağıda verilmiştir. Şifrede (c, d, 4, *} sembolleri ve (1,2,3,4,5) rakamları birer kez kullanılacaktır. ilk üç hanesi rakamlardan ve son 3 hanesi sembollerden oluşan şifreler 6 haneli olacaktır. . Rakamlar büyükten küçüğe doğru sıralanacaktır. Buna göre, Bayram bu siteden kaç farklı şifre alabilir? A) 144 B) 180 C) 210 D) 216 E) 240

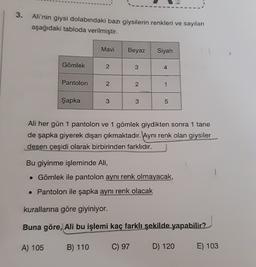
3. Ali'nin giysi dolabındaki bazı giysilerin renkleri ve sayıları aşağıdaki tabloda verilmiştir. Mavi Beyaz Siyah Gömlek 2 3 4 Pantolon 2. 2 1 Şapka 3 3 5 Ali her gün 1 pantolon ve 1 gömlek giydikten sonra 1 tane de şapka giyerek dışarı çıkmaktadır. Aynı renk olan giysiler desen çeşidi olarak birbirinden farklıdır. Bu giyinme işleminde Ali, • Gömlek ile pantolon aynı renk olmayacak, • Pantolon ile şapka aynı renk olacak kurallarına göre giyiniyor. Buna göre, Ali bu işlemi kaç farklı şekilde yapabilir? A) 105 B) 110 C) 97 D) 120 E) 103

ÖSYM ÇIKMIŞ SORULAR - Karma Test 3 4. 1. A = {1, 2, 3} ve B = {2, 3, 4, 5} kümeleri veriliyor. Buna göre, her a E A için a + f(a) = 6 koşulunu sağlayan kaç tane f : A - B fonksiyonu ta- nimlanabilir? A) 12 B) 18 C) 20 D) 24 E) 27 (2014 - YGS)

GÜR YAYINU 2. Bir apartmanda biri 6 diğeri 4 kişilik olmak üzere iki asansör vardır. Elif ile Vesile aynı asansörde bulunmamak koşulu ile 10 kişi asansörlere kaç farklı şekilde binebilir? B) 92 C) 112 D) 118 E) 136 A) 56

2.1 6. Aşağıda doğrusu 2. Bir düzlemde 6 tanesi doğrusal 10 nokta vardır. Buna göre, bu noktalar en fazla kaç doğru belirtir? A) 25 D) 31 E) 33 d, l/d, üçü olar B) 27 C) 29 X. S.4.3 u. 3.7.1 A) 26 3.s=is 7. Aşağıda ri doğru 3. Aşağıdaki şekilde d, ve d, doğruları C noktasında kesiş- mektedir. H de B G F D Köşele lebilir? E di A) 34 Bu doğrular üzerindeki 8 nokta kullanılarak d, ved, dışında birbirinden farklı kaç doğru çizilebilir? 8. Aşağıd A) 12 B) 13 C) 14 D) 15 E) 16 → Be boy 4. Aynı düzlemde bulunan ve herhangi ikisi paralel olmayan 7 farklı doğrunun 3'ü bir A noktasında kesişmektedir. → Bo yad Buna göre, bu 7 doğrunun kesişimi ile en çok kaç farklı nokta oluşur? Buna A) 19 B) 20 C) 21 D) 22 E) 23 A) 9 267