Trigonometrik Fonksiyonların Grafikleri Soruları

Lise Matematik
Trigonometrik Fonksiyonların Grafikleri45. Aşağıdaki dik koordinat düzleminde,
f(x) = sinx ve g(x) = a.sin(bx)
fonksiyonlarının grafikleri verilmiştir. (27) 2
(3)--2
2
1
O
1₁
TU
2
VIT
3πt
D) II ve III
y = g(x)
2T X
y = f(x)
a.sin(16.90) = -1
a sin (5.270) - 2+
ar sin (5123)=0
asin (6360)=0
|AB| = 4 olduğuna göre,
1. la + bl = 2
II. g, fonksiyonunun periyodi 2'dir.
II. g()-1() <0 dir
3
yukarıdaki ifadelerden hangileri doğrudur?
A) Yalnız I
B) I ye III
ORİJİNAL MATEMATİK
9 (²) < (3/
E) I, II ve III
C) I ve 11
47
Lise Matematik
Trigonometrik Fonksiyonların GrafikleriYT-
B
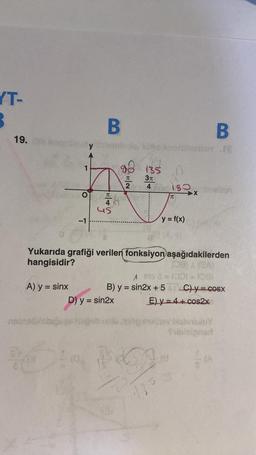
19.
nab
O
A) y = sinx
-1
B
elayo
5
45
E|N
2
D) y = sin2x
135
3π
4
B) y = sin2x + 5
0
180
Yukarıda grafiği verilen fonksiyon aşağıdakilerden
hangisidir?
(08) LEAN
TOPO
TC
y = f(x)
135
X
A ms2=1001 = 10gr
B
any 19
C)y= cosx
E) y = 4 + cos2x.
MabrexuY
Tablelprad
S
(A

Lise Matematik
Trigonometrik Fonksiyonların Grafiklerire,
00
37. Analitik düzlemde, B(0, -8) ve E(0, 8) noktalarından geçen
ABCDEF düzgün altıgeni aşağıda verilmiştir.
F
pour assus man
YA
W OLSUOS WEIBu si prin
E(0,8)
INDEG.COM
0
B(0, -8)
E) || A||
Bu altıgen, orijin etrafında pozitif yönde 150° döndürüldük-
ten sonra x eksenine göre simetriği alınıyor.
Chapuis
BEALGAG SELSLADD
Buna göre, son durumda F noktasının koordinatları aşağıda-
Kopagie
kilerden hangisi olur?
A) (4, 4√3)
Gebo
C) (4,-4√3)
B) (-4,4√3)
D) (4√3, 4) CoE) (4√3,-4) 2
II. OTURUM (AYT) DENEME-3
![Kafa Dengi
5. Dik koordinat düzleminde y = f(x) fonksiyonunun
[0, 2π] aralığındaki grafiği aşağıdaki şekilde
verilmiştir.
2
1
AY
O
E|N
2
R
3π
2
2π
-X
Buna göre, f fonksiyonu aşağıdakilerden
hangisi olabilir?
A) f(x) = 2- |cosx|
B) f(x) = 1 + |cosx|
C) f(x) = 1 + |sinx|
D) f(x) = |sinx|
E) f(x) = |sinx + COSX|](https://media.kunduz.com/media/question/seo/raw/20230106193531225559-4768167.jpg?w=256)
Lise Matematik
Trigonometrik Fonksiyonların GrafikleriKafa Dengi
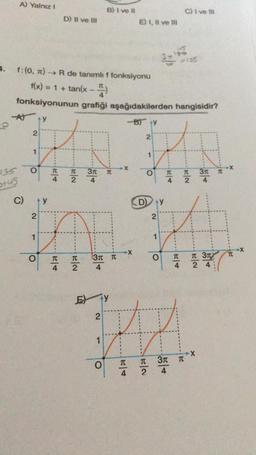
5. Dik koordinat düzleminde y = f(x) fonksiyonunun
[0, 2π] aralığındaki grafiği aşağıdaki şekilde
verilmiştir.
2
1
AY
O
E|N
2
R
3π
2
2π
-X
Buna göre, f fonksiyonu aşağıdakilerden
hangisi olabilir?
A) f(x) = 2- |cosx|
B) f(x) = 1 + |cosx|
C) f(x) = 1 + |sinx|
D) f(x) = |sinx|
E) f(x) = |sinx + COSX|
Lise Matematik
Trigonometrik Fonksiyonların Grafikleri3.
A) Yalnız I
+46
C)
2
1
O
f: (0, π) →→ R de tanımlı f fonksiyonu
f(x) = 1 + tan(x - 2)
fonksiyonunun grafiği aşağıdakilerden hangisidir?
-A) Y
2
1
ty
O
T
D) II ve III
|H|4
TC
2
20
EN
B) I ve il
2
3r T
4
3π π
4
Ey
O
E) I, II ve Ill
X
TC
-B) ty
3-43
D) Y
2
2
HA
O
TC
T
2
1
2
24
1
TC
2
O
C) I ve Ill
#135
TC
4
A
3π π
4
3r
3T
24
X
TC
![Örnek 6
Aşağıda f(x) = a + bsin(cx) fonksiyonunun [0, π] aralığında
grafiği verilmiştir.
3
-1
14
f(x)=a + bsin(cx)
I
2
3r
TC
2 Matematik Planis Ders Föyü
TC
Buna göre, b.c-a ifadesinin değeri kaçtır?
A) 5
B) 4
D) 2
O
Shupe
E) 1
fw
üz
[A
ala
A)](https://media.kunduz.com/media/question/seo/raw/20221227183558195849-3747174.jpeg?w=256)
Lise Matematik
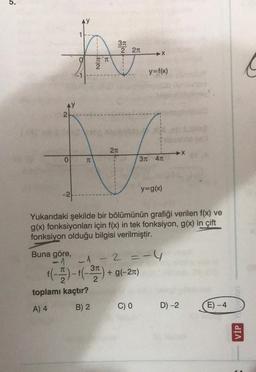
Trigonometrik Fonksiyonların GrafikleriÖrnek 6
Aşağıda f(x) = a + bsin(cx) fonksiyonunun [0, π] aralığında
grafiği verilmiştir.
3
-1
14
f(x)=a + bsin(cx)
I
2
3r
TC
2 Matematik Planis Ders Föyü
TC
Buna göre, b.c-a ifadesinin değeri kaçtır?
A) 5
B) 4
D) 2
O
Shupe
E) 1
fw
üz
[A
ala
A)
Lise Matematik
Trigonometrik Fonksiyonların GrafikleriAY
1
3π
he
2
TC TC
2
AY
2
TU
2π
toplamı kaçtır?
A) 4
B) 2
_1
f(-77-)-f(-37). + g(-2π)
-X
y=f(x)
C) 0
3r 4t
Yukarıdaki şekilde bir bölümünün grafiği verilen f(x) ve
g(x) fonksiyonları için f(x) in tek fonksiyon, g(x) in çift
fonksiyon olduğu bilgisi verilmiştir.
Buna göre,
y=g(x)
-2=-4
X
D) -2
E) -4
11D
VIP
![0. Aşağıda [0, π] aralığında tanımlı bir f fonksiyonunun grafiği
verilmiştir.
nabralbic bundax
2
1
y
O
TC
2
D) sinx + 2
T
1415
1+(1-xSina (0
Buna göre, bu fonksiyonun kuralı aşağıdakilerden
hangisi olabilir?
A) cos2x + 1
B) cosx + 2
C) sin2x + 1
E) sin2x + 2
2](https://media.kunduz.com/media/question/seo/raw/20221220152335203968-2606514.jpeg?w=256)
Lise Matematik
Trigonometrik Fonksiyonların Grafikleri0. Aşağıda [0, π] aralığında tanımlı bir f fonksiyonunun grafiği
verilmiştir.
nabralbic bundax
2
1
y
O
TC
2
D) sinx + 2
T
1415
1+(1-xSina (0
Buna göre, bu fonksiyonun kuralı aşağıdakilerden
hangisi olabilir?
A) cos2x + 1
B) cosx + 2
C) sin2x + 1
E) sin2x + 2
2

Lise Matematik
Trigonometrik Fonksiyonların Grafikleri27.
Şekilde verilen dik koordinat düzleminde, xOy düzlemi ile
orijinleri çakışık x'Oy' düzlemi oluşturuluyor.
x' ve y' sırasıyla y = x ve y = -x doğruları üzerindedir.
Buna göre, xOy düzlemindeki x = 2 doğrusunun x'Oy!
düzleminde eğimi kaçtır?
A)=1/12 B)
Ay
13
C)
√√2
D) 1 E) -1
![Yukarda (o saranda grange
Soru
caxs
13
0
Çözüm
-3
da grafigi veren fonksiyonu bulalo
2 sioX+)
+1
AV
y= = f(x)
(fola) 8
Yukarıda [0, 1] aralığında grafiği verilen fonksiyonu bulalım.
Tanjant ve Kotanjant Fonksiyonlarının Grafikleri
f: R. -{+k+x)→R (k=Z) ve f(x) = tanx fonksiyon
y = tanx denkleminin grafiği aşağıdaki gibidir.
y = tanx](https://media.kunduz.com/media/question/seo/raw/20221211132852734290-3757233.jpg?w=256)
Lise Matematik
Trigonometrik Fonksiyonların GrafikleriYukarda (o saranda grange
Soru
caxs
13
0
Çözüm
-3
da grafigi veren fonksiyonu bulalo
2 sioX+)
+1
AV
y= = f(x)
(fola) 8
Yukarıda [0, 1] aralığında grafiği verilen fonksiyonu bulalım.
Tanjant ve Kotanjant Fonksiyonlarının Grafikleri
f: R. -{+k+x)→R (k=Z) ve f(x) = tanx fonksiyon
y = tanx denkleminin grafiği aşağıdaki gibidir.
y = tanx

Lise Matematik
Trigonometrik Fonksiyonların Grafikleri=(2.-3)
=(-4-2) 5. A(n+1,2) noktasının y eksenine olan uzaklığı x
=(-1,3)
alzanine lan uzak 3 katı olduğuna göre,
in nin alabileceği değerler toplamı kaçtır?
8)-1 010 012
7.
8.
5.
9.
A)-2
A) 2
A) B
40-2)
A) 2
Anaillik düzlemde verilen ABCD karesinin C kü-
şesinin ordinatı kaçtır?
B) 4
A)1
£6
B) 10
TEE, 0) X
B
B) 3
C) 6
Analitik düzlemde köşe koordinatlanı,
A(1,4), B(4,4), C(4,-1) ve D(1,-1)
olan geometrik şeklin çevresi kaç br dir?
C) 12 D) 14
E) 16
D) 8
E4
A(m-2, 6-m) noktası analitik düzlemin
1. bölgesinde olduğuna göre, m kaç farklı tam-
sayı değeri alabilir?
ABCD kare
A(0, -2)
E(6,0)
C) 4 D) 5
E) 10
C) III D) IV
A(a, -b) noktası analitik düzlemin 1. bölgesinde
olduğuna göre, B(a +3, b-1) noktası hangi
hölganlarin
E) 6
E) Orijin

Lise Matematik
Trigonometrik Fonksiyonların Grafikleri12.
f(x) = 7 -tan5(-8x + 1)
fonksiyonu veriliyor.
Buna göre,
A)
f(x) = f(x + T)
eşitliğini sağlayan en küçük T pozitif gerçel sayıs
kaçtır?
T
7
B)
TC
15
(C)
TC
T=IT
8
4
p)
T
8
E)
2π
7
T.C. Milli Eğitim Bakanlığı / Muratpaşa İlçe Milli Eğitim Müdürlüğü
![x) = cos3x fonksiyonunun grafiği [-2, 2] aralığında aşağıdakilerden hangisidir?
i
D)
70
AS
KS
B)
-2x-3-
4K
S
2n
10
2
T
R
3n 2n
2
E)
-2R
C)
-3r
2
It
2
3K
AY
O
AA
1
2n
aralık
a) Sinüs Fonksiyonu
TC TC
KIN
sin :
[-1. 1]; bire
2 2
f(x) = sinx fonksiyonunun te
r1(x) = arcsinx tir.
-22
AY
70
2
sin
1
Buna göre,
arcsin: [-1, 1] →
ÖRNE
12
TO
6 2
Not](https://media.kunduz.com/media/question/seo/raw/20221205092759257264-4678039.jpeg?w=256)
Lise Matematik
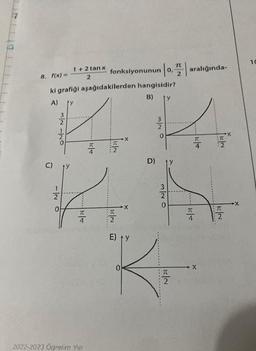
Trigonometrik Fonksiyonların Grafiklerix) = cos3x fonksiyonunun grafiği [-2, 2] aralığında aşağıdakilerden hangisidir?
i
D)
70
AS
KS
B)
-2x-3-
4K
S
2n
10
2
T
R
3n 2n
2
E)
-2R
C)
-3r
2
It
2
3K
AY
O
AA
1
2n
aralık
a) Sinüs Fonksiyonu
TC TC
KIN
sin :
[-1. 1]; bire
2 2
f(x) = sinx fonksiyonunun te
r1(x) = arcsinx tir.
-22
AY
70
2
sin
1
Buna göre,
arcsin: [-1, 1] →
ÖRNE
12
TO
6 2
Not
Lise Matematik
Trigonometrik Fonksiyonların Grafikleri8. f(x) =
ki grafiği aşağıdakilerden hangisidir?
B)
A) ty
1
T
1+2tanx fonksiyonunun [0, aralığında-
2
3/2 120
TC
2022-2023 Öğretim Yılı
4
Sovietm
|K|N
TC
2
-X
X
E) ty
0
D)
M/NO
M/NO
K
E|N
2
TC
TC
TC
12
EN
2
X
-X
10
Lise Matematik
Trigonometrik Fonksiyonların Grafiklerib,
-)
en
M
MATEMATIK
(M)
MATEMATIK
SORU
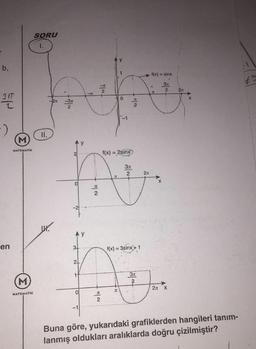
1.
1
-f(x) = sinx
ho
0
2
II.
2
0
3
H2
I
FIN
f(x)=2sinx
1
3x
2
2x
3t
2
f(x) = 3sinx+1
AD
3.T
2 X
2x
Buna göre, yukarıdaki grafiklerden hangileri tanım-
lanmış oldukları aralıklarda doğru çizilmiştir?
![25. f(x)=1+2 sinx
fonksiyonunun [-,] aralığında grafiği aşağıdakiler-
den hangisidir?
A)
B)
D)
E)
- TO
- TC
17
- T
R
72
-22
-----
-22
TU
3
1
-1
3
3
1
0
-1
y
ty
10
-1
>
10
-1
10
10
-3
TU
2
EN
TC
2
TC
2
EN
2
2
TU
TU
It
TC
I
X
X
X](https://media.kunduz.com/media/question/seo/raw/20221129184558736018-923993.jpg?w=256)
Lise Matematik
Trigonometrik Fonksiyonların Grafikleri25. f(x)=1+2 sinx
fonksiyonunun [-,] aralığında grafiği aşağıdakiler-
den hangisidir?
A)
B)
D)
E)
- TO
- TC
17
- T
R
72
-22
-----
-22
TU
3
1
-1
3
3
1
0
-1
y
ty
10
-1
>
10
-1
10
10
-3
TU
2
EN
TC
2
TC
2
EN
2
2
TU
TU
It
TC
I
X
X
X
