Birebir Örten Fonksiyon Soruları

Lise Matematik
Birebir Örten Fonksiyon2
xtb
And
g
7
TYT/Temel Matematik
15. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
C
22
O
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 95 96 97 98 99
17
A = {0, 1, 2, 3, ..., 99}
B = {0, 1, 2, 3, ..., 22}
olmak üzere, A kümesinden B kümesine tanımlanan
f(x): (x! sayısının sonundaki sıfır sayısı" fonksiyonu
için
flats
I. f fonksiyonu bire birdir
II. f fonksiyonu örtendir.
III. f(a)=4 ve f(b) = 6 koşulunu sağlayan a ve b değerle-
ri için b - a farkının alabileceği en küçük değer 1'dir.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
D) I ve II
y = f(x)
EII ve III
20 21 22 23 24 74
25
26 27 28 2
30
31 32 33 34 4
Yalnız III
16. p bir asa
sayı değ
3
Ömeğin
dan izole
Buna g
izole as
A) 29
12/3
1515435
17. Bir veri g
landığınd
çift ise or
grubunun
Küçükten
n+1
2
veri grubu
yanı değis
Buna ga
kaçtm?
A) 17
n+4=
![12.
3
2
1
ol
1
C
I
D) II ve III
2
3
H
f: [0, 5] → [0, 3] fonksiyonunun grafiği yukarıda verilmiştir.
Buna göre 2. f(x) = x denkleminin,
I.
(0, 1)
II. (3, 4)
III. (4,5)
aralıklarının hangilerinde en az bir kökü vardır?
A) Yalnız I
B) Yalnız II
4 5
E) I, II ve III
C) Yalnız III](https://media.kunduz.com/media/question/seo/raw/20230220104431169121-2681136.jpg?w=256)
Lise Matematik
Birebir Örten Fonksiyon12.
3
2
1
ol
1
C
I
D) II ve III
2
3
H
f: [0, 5] → [0, 3] fonksiyonunun grafiği yukarıda verilmiştir.
Buna göre 2. f(x) = x denkleminin,
I.
(0, 1)
II. (3, 4)
III. (4,5)
aralıklarının hangilerinde en az bir kökü vardır?
A) Yalnız I
B) Yalnız II
4 5
E) I, II ve III
C) Yalnız III

Lise Matematik
Birebir Örten Fonksiyon1.
Alican futbol to-
punu iple bağ-
layıp bir ucunu
tavana sabitle-
yip A noktasın-
dan serbest bi-
rakmıştır. Ali-
can topun A
noktasından ilk
defa durduğu
ana kadar geçen zamanı 4 sn olarak ölçmüştür.
0 ≤ x ≤ 4 olmak üzere, f(x), x. saniyede topun
yerden yüksekliği olarak tanımlanırsa f fonksi-
yonu için aşağıdakilerden hangisi daima doğ-
rudur?
Diary
D) I, IL
A. f birebir fonksiyondur.
LH 0≤x≤ 1 için f azalandır.
III. f(x)=y ise f(x) = y olacak şekilde
farklı en az bir tane x₂ değeri vardır.
A)H
B) II
C) III
E) II, III
den
4. f(x)=-
23
ayınları
olduğu
lerden
A) (-8
5. Şeki
mişt
Lise Matematik
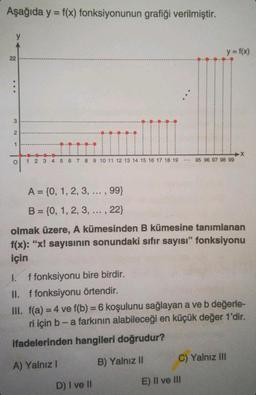
Birebir Örten FonksiyonAşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
y
22
3
2
1
O
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
:
D) I ve II
y = f(x)
95 96 97 98 99
A = {0, 1, 2, 3, ..., 99}
B = {0, 1, 2, 3, ..., 22}
olmak üzere, A kümesinden B kümesine tanımlanan
f(x): "x! sayısının sonundaki sıfır sayısı" fonksiyonu
için
E) II ve III
1. f fonksiyonu bire birdir.
II. f fonksiyonu örtendir.
III. f(a) = 4 ve f(b) = 6 koşulunu sağlayan a ve b değerle-
ri için b - a farkının alabileceği en küçük değer 1'dir.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
-X
C) Yalnız III

Lise Matematik
Birebir Örten FonksiyonTesti için ayrılan kısm
E) 54
ayılar
tedir.
lari
3. a, b, c ve d tam sayılar olmak üzere,
sayıları küçükten büyüğe ardışık tam sayılardır.
a-b, b + c ve c - d
Buna göre,
I.
II. a + c tek sayıdır.
III. b-d tek sayıdır.
ifadelerinden hangileri kesinlikle doğrudur?
A) Yalnız I
B) Yalnız II
ab çift sayıdır.
D) II ve III
E) Yalnız III
5.
Kısa
üçgenin hipotenüsü
a
Alanı S birim
ABCD ve EF
EFHK kare
olduğuna
aşağıdak
A) √a

Lise Matematik
Birebir Örten Fonksiyon1.
Test-1
f: AA ve g: A → A
biçiminde tanımlanmış fonksiyonlar veriliyor.
fog(x) fonksiyonunun örten, gof(x) fonksiyonunun ise
birebir olduğu biliniyor.
Buna göre,
D) I ve III
(x)=x² g/x/= x^
Reinoviaxnot exigatid
8 (1)
I. f(x) fonksiyonunun tersi vardır.
Tutos e me) (in
II. g(x) fonksiyonunun tersi vardır.
8 (III. f¹og(x) fonksiyonu örtendir.
yargılarından hangileri kesinlikle doğrudur?
A) Yalnız I
B) Yalnız II
C) Yalnız III
E) II ve III
B
13k42

Lise Matematik
Birebir Örten FonksiyonB B
29. A, B ve C boş olmayan sonlu üç kümedir.
• A'dan B'ye tanımlı f fonksiyonunun tersi de bir
fonksiyondur.
Ghi
B'den C'ye tanımlı g fonksiyonu içine fonksiyondur.
•
Buna göre,
TYT DENEME SINAVI 04
I. s(A) = s(B)
II. s(B) ≤ s(C)
III. s(A) <s(C)
ifadelerinden hangileri kesinlikle doğrudur?
B) Yalnız III
A) Yalnız I
D) II ve III
C) I ve II
E) I, II ve III
*D÷1
![32.
TE
sbrimsieblon 8/A alti
A(-3, 5)
D
B(2,-5)
C(4,0)
Şekilde [AB] n [CE] = {D}, 3IADI = 2IBDI,
IDEI = 2ICDI, A(-3, 5), B(2, -5), C(4, 0)
olduğuna göre, E noktasının koordinatları çarpımı kaçtır?
A) -45 B) -39 C) -33 D) -27 E) -24](https://media.kunduz.com/media/question/seo/raw/20230219071714441267-4647550.jpg?w=256)
Lise Matematik
Birebir Örten Fonksiyon32.
TE
sbrimsieblon 8/A alti
A(-3, 5)
D
B(2,-5)
C(4,0)
Şekilde [AB] n [CE] = {D}, 3IADI = 2IBDI,
IDEI = 2ICDI, A(-3, 5), B(2, -5), C(4, 0)
olduğuna göre, E noktasının koordinatları çarpımı kaçtır?
A) -45 B) -39 C) -33 D) -27 E) -24

Lise Matematik
Birebir Örten Fonksiyonmesindeki
n B ye ta
\))
m)
1.
A ve B kümelerinin eleman sayıları sırasıyla a ve b olmak üzere,
A dan B ye tanımlanabilecek; fonksiyon sayısı b, bire bir fonk-
(b2a), sabit fonksiyon sayısı b, bire bir
siyon sayısı
bl
(b-a)! "
Fonksiyonlar
ve örten fonksiyon sayısı al (aby dir.
A - (a, b, c)
(91) (4)
B-(1,2,3)
olmak üzere, aşağıdakilerden hangisi yanlıştır?
AA'dan B'ye 27 tane fonksiyon tanımlanabilir.
B) A'dan B'ye 6 tane bire bir fonksiyon tanımlanabilir.
A'dan B'ye 3 tane sabit fonksiyon tanimlanır. +
D) B'den B'ye 21 tane içine fonksiyon tanımlanır.
E))A'dan A'ya 9 tane örten fonksiyon tanımlanır.
R-R ve a, b reel sayı olmak üzere, f
deki fonksiyonlara doğrusal fonksiyon deni
y=f(x) orijinden geçen doğrusal bir fonks
1(16)-1(14) = 6 6lduğuna göre, 1
1(1)+1(2)+1(3)+...+1(15)
toplámı kaçtır?
A) 420
B) 400
f(16)-f(14) = 6
169-149-6
2a=6
a=)
C) 360
f(1) =>
f(3) =
5. Tanım kümesinin alt aralıklarında f
fonksiyonlara parçalı fonksiyon den
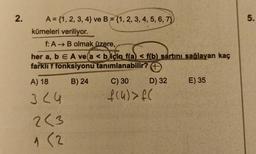
Lise Matematik
Birebir Örten Fonksiyon2.
A = {1, 2, 3, 4) ve B = {1, 2, 3, 4, 5, 6, 7)
kümeleri veriliyor.
f: A → B olmak üzere,
her a, b E A ve a < b için f(a) f(b) sartını sağlayan kaç
farklı f fonksiyonu tanımlanabilir? +
A) 18 B) 24
324
2<3
1 (2
C) 30
f(4) > f(
D) 32
E) 35
5.
![il vodafone TR
6.
18:39
→]
A'dan B'ye tanımlı birebir ve örten bir fonksiyonda
s(A) + s(B) = 8
olduğu bilinmektedir.
Elemanları pozitif tam sayılar olan A kümesinin
elemanları toplamı en az kaçtır?
A) 4
B) 6
C) 8
X
1 @ %98
D) 10
E) 15
C
a ve](https://media.kunduz.com/media/question/seo/raw/20230217153954736340-4678039.jpeg?w=256)
Lise Matematik
Birebir Örten Fonksiyonil vodafone TR
6.
18:39
→]
A'dan B'ye tanımlı birebir ve örten bir fonksiyonda
s(A) + s(B) = 8
olduğu bilinmektedir.
Elemanları pozitif tam sayılar olan A kümesinin
elemanları toplamı en az kaçtır?
A) 4
B) 6
C) 8
X
1 @ %98
D) 10
E) 15
C
a ve

Lise Matematik
Birebir Örten FonksiyonC) -2.0.1.2.3)
11.
-4
10 ff birim fonksiyon olmak üzere,
-4 f(2x + 3) = (a + 1x² + (b-2)x+ a-b.c
3 ise a b-c değeri kaçtır?
3
A)-64 B)-5
C) -3
atle=
a=-1
Girdi
6-2-2
b=l
Ey6.1.2
1, 2, 3, 4)
f
DT, 2, 3, 4, 5)
5₁-2²
(D) 4
@-b.c=3
22
C
4-5.2=3
batu
Çıktı
5x2 - 2
3--1-1
A) 18 B) 21) C) 24
2²-2
5.-2
Fonksiyon konusunun anlatıldığı bir matematik
dersinde öğretmen, üstteki makine örneğini yap-
mıştır. Daha sonra sınıftan iki öğrencinin bu maki-
neye iki farklı sayı atmasını istemiştir.
Makineye girilen sayılar sırasıyla -2 ve 1 oldu-
ğuna göre çıktıların toplamı kaçtır?
D) 27
E) 6
241
5--4-2
0-3 <=1
3
E) 30
Bu testin cevap anahtan arka saytadadır
203

Lise Matematik
Birebir Örten Fonksiyon4.
3. f:R-{1} → R-{3} olmak üzere,
ax +4
X-1
olduğuna göre, a kaçtır?
A) -3
f(x)=
A) -3
B)-2
f:R-{a} → R-{b} olmak üzere,
2x + 4
3x - 1
f(x) =
C) -1
B) -2
fonksiyonu birebir ve örten olduğuna göre, a+b
toplamı kaçtır?
Konu Kavrama Serisi
D) 1
C) -1
E) 3
D) 1
E) 2
7.
132
8.
![23.
24.
fu W
a
Yukarıda f: R→→ R olmak üzere, y = f(x) fonksiyonunun [0, a]
aralığındaki grafiği verilmiştir.
A) 9
y = f(x)
Bu fonksiyon tüm reel sayılar için bir çift fonksiyon olma
özelliğine sahip olduğuna göre f(x) = 0 eşitliğini sağlayan
en az kaç farklı x değeri vardır?
B) 8
C) 7
D) 6
E) 5](https://media.kunduz.com/media/question/seo/raw/20230215161418638792-5110168.jpeg?w=256)
Lise Matematik
Birebir Örten Fonksiyon23.
24.
fu W
a
Yukarıda f: R→→ R olmak üzere, y = f(x) fonksiyonunun [0, a]
aralığındaki grafiği verilmiştir.
A) 9
y = f(x)
Bu fonksiyon tüm reel sayılar için bir çift fonksiyon olma
özelliğine sahip olduğuna göre f(x) = 0 eşitliğini sağlayan
en az kaç farklı x değeri vardır?
B) 8
C) 7
D) 6
E) 5
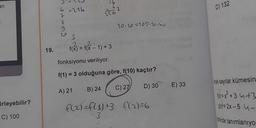
Lise Matematik
Birebir Örten Fonksiyonan
irleyebilir?
C) 100
19.
6 =216
etwoord
10
36.
3
f(x) = f(x-1) + 3
3
10.10=102.104
fonksiyonu veriliyor.
f(1) = 3 olduğuna göre, f(10) kaçtır?
C) 27
D) 30 E) 33
A) 21 B) 24
f(x)=f(1) +3 f(2)=6
~3
D) 132
pek sayılar kümesin
8x²= x² +34 +3
glx=2x-54-
minde tanımlanıyo

Lise Matematik
Birebir Örten FonksiyonAşağıdakilerden
Af: Z→Z,
Bf: N→N,
f: R→R,
Df: R→R,
1: Z→Z,
hangisi 1-1 ve örten bir fonksiyondur?
f(x) = 2x - 3
f:2 → 2 örten olm. ic
f(x)=1₁x + a
f(x) = x + 4
f(x)=-1.x+b
f(x) = x²
f(x) = x³ atlays
atlaya
gidiyor.
f(x) = (3x + 1
N
2
2
N
son
X²;
atlaya atlaya g
