Bölünebilme Kuralları Soruları

2. Eyfel Kulesi, 1887 - 1889 tarihleri arasında inşa edil- miştir. Fransa'nın Paris şehrinde bulunan Demir Leydi lakaplı kulenin yük- sekliği 32x metredir. Şekildeki kartpostalda Eyfel Kulesi'nin yüksekliğine ait üç basamaklı sayının birler basamağındaki rakam matbaa ha- tası nedeniyle x olarak çıkmıştır. Eyfel Kulesi'nin yüksekli- ğinin hem 3'ün hem 4'ün katı olan bir sayı olduğu bilinmek- tedir. Buna göre, x kaçtır? A) O B) 2 C) 4 D) 6 E) 8

5. Beş basamaklı 77A4B sayısının 36 ile bölümünden kalan 25 olduğuna göre, A nın alabileceği değerler toplamı kaçtır? B) 7 A) 6 C) 9 73A41 77445 19+9=52²-8 23+3=564² 3 rt 18 D) 11 E) 13 A3 A4974 27+1=54896 DE

.. ... ... D) 450 ... .. Şekil - 1 Şekil - II Şekil - III Ersin, elinde bulunan küpleri birer yüzeyleri çakışacak bi- çimde Şekil 1, Şekil 2 ve Şekil 3'deki gibi ayrı ayrı dizdi- ğinde hiç küp artmıyor. E) 480 .. Ersin'in küplerinin sayısı 500'den az olduğuna göre, Ersin'in en çok kaç küpü vardır? A) 300 B) 360 C) 400 ACILE 12.

1. 23456 saniyelik açı ölçüsünün derece, dakika ve saniye türünden eşiti aşağıdakilerden hangisidir? A) 5° 30' 10" C) 6° 30' 56" E) 7° 30' 01" 234561 60 B) 5° 30' 16" D) 6° 36' 06" 374 160 300 5 256 Açı Ölçü Birimleri 4. 1. 150 derece- F 11. 240 derece= St Il 315 derece-m Yukarıdaki eşitliklerd A) Yalnız il D) II ve III B

6. Her rakam adeti kadar yanyana yazılarak K = 122333 ... 99 ... 9 biçiminde 45 basamaklı bir sayı elde ediliyor. Buna göre, 1 sayısının 5 ile bölümünden 4 kalanını vermektedir. II. K sayısının 9 ile bölümünden 6 kalanını vermektedir. III. K sayısının 20 jle bölümünden 19 kalanını vermekte- dir. 10 12 9 +1 ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II D) II ve III E) I, II ve III C) I ve Il 54 8.

mir 6 A 8. 120 tane çikolatanın tamamı n kişilik bir sınıfa K aşağıdaki koşullara uygun olarak dağıtılacaktır. • Her öğrenci eşit sayıda çikolata alacaktır. • Her öğrenci en az 3, en fazla 20 çikolata ala- caktır. Buna göre, sınıftaki öğrenci sayısı (n) kaç farklı değer alabilir? A) 6 B) 9 C) 12 D) 15 Diğer sayfaya geçiniz. A A A A A A A

1 2 Örnek-19 n kenarlı düzgün bir çokgen içine yazılan x pozitif tam sayısının değeri x sayısı, n sayısına tam bölünüyorsa x sayısı, n sayısına tam bölünmüyorsa O'a eşittir. Örneğin, Buna göre, 45 40 = 0 = 10 20 = 22 eşitliğini sağlayan x değerlerinin toplamı kaçtır? A) 132 B) 192 E) 333 C) 242 D) 302 ? Z Örnek-20 x bir doğal sayı olmak üzere, x+5X+4

a b c dl A) 36 120 a b cd B) 32 336 a b C Yukarıda üç farklı öğrencinin yaptığı işlemler verilmiştir. ab ve cd iki basamaklı doğal sayılar olmak üzere, > 1. işlemi yapan öğrenci yanlışlıkla ikinci satırı bir basamak sağa kaydırıp bu şekilde sonucu 120 bulmuştur. II. işlemi yapan öğrenci doğru sonuç bulduğuna göre, III. işlemi doğru yapan öğrenci sonucu kaç bulmuştur? C) 27 sonuç 56 D) 24 E) 18

9. • a ve b birer doğal sayıdır. ● EBOB(a + 5, 2b - 1) = 9 a +5 3 2b - 1 5 olduğuna göre, a - b farkı kaçtır? A) -1 B) 0 C) 1 10. Pozitif x ve y tam sayıları için; Toplamları 52 dir. En büyük ortak böleni 4 tür. En küçük ortak katı 120 dir. 50+25=6b-3 a+5=3k 26-1=52 ifadeleri bilinmektedir. D) 2 E) 3 x+y=52 EBOB = 4 24. 32 Ba UO - TR Buna göre, x - y farkı aşağıdakilerden hangisi olabilir? A) 30 (B) 28 C) 26 D) 24 KBB) 12. E) 22 52-24-128 13

11. Aşağıda bir oto galerinin vitrininde satılık olan araçlar ve kendilerine özel bir kodlama sistemine göre araçların kodlanı verilmiştir. 124 3+ M A) 9 7 900 181 10 B) 8 542 Bu galeriele satış temsilcisi (S.T) ile müdür (M) arasında aşağıdaki konuşma geçmiştir. M: Mart ayında hangi araçlar satıldı? S.T: Kod numaralarının rakamlarının toplamı asal sayı olan araçlar satıldı. C) 7 ^^ 861 113 300 D) 6 S 346 13 m M: Nisan ayında hangi araçlar satıldı? S.T: Mart ayında satılmayan araçlar arasından kod numarası satılamayan diğer araçların kod numaraları ile aralarında asal olan araçlar satıldı. Yukarıdaki diyaloğa göre, Mart ve Nisan aylarında toplam kaç araba satılmıştır? 6 689 23 Mart asal.

r? E); Deneme - B xyOxy7 sayısı altı, xy sayısı ise iki basamaklıdır. xy0xy7 sayısının xy ile bölümünde bölüm m kalan n oldu- ğuna göre, m + n değeri kaçtır? A) 107 B 1007 D) 10107 100 10+ E) 110017 C) 10017 10107 9. 3-5 Dört basamaklı A4BC sayısının 15 ile bölümünden kalan 8 dir. Buna göre, A8BC sayısının 15 ile bölümünden kalan kaç- 1543 fır?

6. Aşağıda merkezleri aynı olan ve üzerinde eşit aralıklarla rakamlar yazılmış küçük ve büyük iki çarktan oluşan hareketli bir düzenek verilmiştir. Bu düzeneğin üzerine sabit bir numaratör takılmıştır. 12 sn 60 3s 10 A) 10 9 küçük 8 B) 11 1 10 0 9 11 7 11 2 9 10 8 9 Ok yönünde sabit hızlarla hareket eden bu iki çarktan küçük, saniyede 30 dönmektedir. Küçük çark bir tam tur döndüğünde büyük çark 60° dönmektedir Örneğin; başlangıçtan itibaren 6 saniye sonra düzenekte aşa- ğıdaki görünüm elde edilmekte ve numaratör 9 görülmektedir. 1 biçiminde 9000 KE 0 0 16 3 Başlangıç 5 8 5 4 7 8 HO 9 3 6 C) 11 2 3 1 0 4 9 3 6 Başlangıçtan 90 saniye sonra numaratörün görünümü aşağı- dakilerden hangisi gibi olur? Moler 5 /sn 30 2sr D) 9 6 Gro gosh 27009060 Foo 9 9

5. M ve N birer doğal sayıdır. M+2 4 6 N-3 N+5 - 5 2 3 Yukarıdaki bölme işlemlerine göre M sayısı kaçtır? A) 32 B) 41 C) 56 D) 78 E) 99 munden kalan kac A) O B) 3 12. 6 ya, 8 e ve 9 a küçük iki bas hangisine tac A) 7 B 13. Yaşar'ın 2

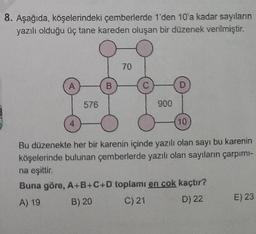
8. Aşağıda, köşelerindeki çemberlerde 1'den 10'a kadar sayıların yazılı olduğu üç tane kareden oluşan bir düzenek verilmiştir. A 4 576 B 70 C 900 D 10 Bu düzenekte her bir karenin içinde yazılı olan sayı bu karenin köşelerinde bulunan çemberlerde yazılı olan sayıların çarpımı- na eşittir. Buna göre, A+B+C+D toplamı en çok kaçtır? A) 19 B) 20 C) 21 D) 22 E) 23

7. TYT hazırlık için hazırlanan bir soru bankasında 26 ünite, her ünitede 8 bölüm, her bölümde 15 test ve her testte 14 soru bulunmaktadır. Buna göre, bu soru bankasındaki toplam soru sayısı aşağıdakilerden hangisine eşittir? 8! A) 31 3! 14! B) 10! C) 16! 10! D) 15! 16! E) 10

ON 00 1 85/ ssul/ 12 7 5 2 10 Büyükten küçüğe doğru sıralı yukarıdaki şekilde, en solda bulunan sayının, sağ yanındaki sayıya bölümün den elde edilen kalan onun sağ yanına yazılmıştır. Da- ha sonra aynı işlem sağ tarafa doğru tekrarlanarak so- nunda sıfır sayısına ulaşılmıştır. 50000 150 a b C Buna göre, yukarıdaki dairelerin içleri bu şekilde doğal sayılarla doldurulduğunda en büyük a de- ğeri için b + c toplamı kaçtır? A) 6 B) 10 C) 15 D) 22 E) 28 X 11.