Ekstremum Noktalar Soruları

Lise Matematik
Ekstremum Noktalar34.
Birbirine dik doğruların eğimleri
çarpımı -1 dir.
Bir dikdörtgenin birbiriyle kesişen iki kenarı,
d₁ : x-2y + 6 = 0 ve
A) -2
doğruları üzerinde yer almaktadır.
Buna göre, a kaçtır?
B)
d₂: ax + y - 3=0
-
11/22
(0) 1/1/201
D) 2
E) 3

Lise Matematik
Ekstremum Noktalar6. a, b ve c birbirinden farklı tam sayılardır.
a<0<b
- 2 + b = 0_41
a+b=0
75
+ 48
627
olduğuna göre, c sayısının eşiti aşağıdakilerden
hangisi olabilir?
A9
B) 4
DENEME-2
CO
D) -4
Oksijen Yayınları
E)-6
8-10
A) a
19
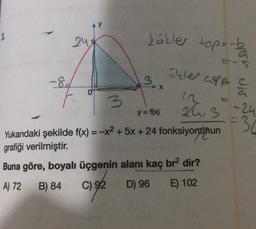
Lise Matematik
Ekstremum Noktalar3.
-8d
248
3
kökler top=-be
3xx
X
aller coppa e
12
24.3
y = f(x)
Yukarıdaki şekilde f(x) = -x² + 5x + 24 fonksiyonunun
grafiği verilmiştir.
Buna göre, boyalı üçgenin alanı kaç br² dir?
A) 72 B) 84
C) 92
D) 96
E) 102
-24
=36

Lise Matematik
Ekstremum Noktalar19. m ve n gerçel sayılar olmak üzere,
x³
f(x) = +mx² + (n-4)x+2m-n
3
fonksiyonu ile ilgili aşağıdakiler bilinmektedir; uğublo
f'(-3) = 0 dir.
f(x) in yerel ekstremumu yoktur.
●
012
Buna göre, n − m farkı kaçtır?
A) 9
B) 10
C) 11
Matematik
D) 12
EXIS
E) 13
let pov: SS
![larda Uygulamalar
-5
-3
-1
YA
1
-3
0
1
3
y=f(x)
III. [-5, -1] aralığında artandır.
IV. [-1, 1] aralığında azalandır.
V. [1, 4] aralığındaki değişim hızı
A) 1
B) 2
C) 3 D) 4
f: [-5, 4] → [-3, 3] olmak üzere yukarıda grafi-
ği verilen y = f(x) fonksiyonu için aşağıdakiler-
den kaç tanesi doğrudur?
4
I. Yerel maksimum değerleri 1 ve 3 tür.
II. Yerel minimum değerleri 0 ve -3 tür.
4
3
tür.
E) 5](https://media.kunduz.com/media/question/seo/raw/20230225190227323045-4080292.jpeg?w=256)
Lise Matematik
Ekstremum Noktalarlarda Uygulamalar
-5
-3
-1
YA
1
-3
0
1
3
y=f(x)
III. [-5, -1] aralığında artandır.
IV. [-1, 1] aralığında azalandır.
V. [1, 4] aralığındaki değişim hızı
A) 1
B) 2
C) 3 D) 4
f: [-5, 4] → [-3, 3] olmak üzere yukarıda grafi-
ği verilen y = f(x) fonksiyonu için aşağıdakiler-
den kaç tanesi doğrudur?
4
I. Yerel maksimum değerleri 1 ve 3 tür.
II. Yerel minimum değerleri 0 ve -3 tür.
4
3
tür.
E) 5
Lise Matematik
Ekstremum Noktalar6
18.
-3
1
A) 13
AY
5
-5
3
2
B) 11
vor
f(x) = y
6 7
Min
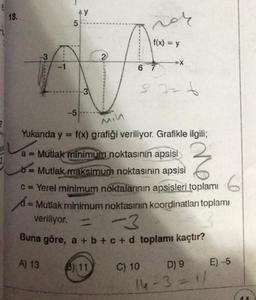
Yukarıda y = f(x) grafiği veriliyor. Grafikle ilgili;
a = Mutlak minimum noktasının apsisi
b = Mutlak maksimum noktasının apsisi
c = Yerel minimum noktalarının apsisleri toplamı
Z
X
= Mutlak minimum noktasının koordinatları toplamı
veriliyor. = -3
Buna göre, a + b + c + d toplamı kaçtır?
C) 10
sarb
D) 9
14-3=1/
E) -5

Lise Matematik
Ekstremum Noktalar-3-2
1
O
3
2
1
by = f(x)
3
X
Buna göre aşağıdaki ifadelerin hangile-
ri yanlıştır?
Yukarıda [-4,3) nda tanımlı y = f(x)
fonksiyonunun grafiği verilmiştir.
I.
f fonksiyonunun 4 tane ekstremum
noktası vardır.
II. f(x) fonksiyonunun mutlak minimum
değeri 1 dir.
III. f(x) fonksiyonunun mutlak maksimum
değeri 6 dır.
IV. f(x) fonksiyonunun yerel maksimum
değerleri toplamı 14 tür.
V. f(x) fonksiyonunun yerel minimum
değerleri toplamı 5 tir.
A)I ve III
B)I ve IV
D) II ve V
C) II ve IV
E) IV ve V

Lise Matematik
Ekstremum Noktalar6=0
21. Gerçek sayılar kümesinde tanımlı
x²+4x, x≤0
-x²+6x, x>0
fonksiyonu veriliyor.
Buna göre,
1. f fonksiyonu (-2, 3) aralığında artandır.
11. (-4,-2) aralığında negatif değerli ve artandır.
III. f(x)'in minimum ve maksimum değerleri toplamı 5'tir.
yargılarından hangileri doğrudur?
A) Yalnız 1
B) Yalnız II
D) II ve III
E) I ve Ill
C) I, II ve III
AYT DENEME-1

Lise Matematik
Ekstremum Noktalark bir pozitif gerçek sayı olmak üzere, gerçek sayılar
kümesi üzerinde bir f fonksiyonu
kx
x² +1
biçiminde tanımlanıyor.
f(x) =
V
f fonksiyonunun yerel maksimum değeri 5 oldu-
ğuna göre, k değeri kaçtır?
A) 5
Ⓡ10
C) 15
D) 20
E) 25
Ar
![in-
2
4
a
i
1
1
1
1
1
1
1
1
1
3
1
1
I
1
1
1
1
1
1
1
99
11.
(-1,2)
€102
(sabab)
-3-2
-1
|
-3
(mo)laxy
B) -3 C) -2
(exab)
2 T
-4
Br
08
−4+2=2
1 2
a
3
D) 2
4
0
y = f(x)
X=U
ST 0
(-3,-4)
Yukarıdaki şekilde grafiği verilen ve [-4, 4] aralığın-
da tanımlı olan f(x) fonksiyonunun yerel minimum
ve yerel maksimum noktalarının ordinatlarının top-
lamı kaçtır?
A)-5
X
E) 3
Kafa Dengi](https://media.kunduz.com/media/question/seo/raw/20230218123645107663-1764483.jpeg?w=256)
Lise Matematik
Ekstremum Noktalarin-
2
4
a
i
1
1
1
1
1
1
1
1
1
3
1
1
I
1
1
1
1
1
1
1
99
11.
(-1,2)
€102
(sabab)
-3-2
-1
|
-3
(mo)laxy
B) -3 C) -2
(exab)
2 T
-4
Br
08
−4+2=2
1 2
a
3
D) 2
4
0
y = f(x)
X=U
ST 0
(-3,-4)
Yukarıdaki şekilde grafiği verilen ve [-4, 4] aralığın-
da tanımlı olan f(x) fonksiyonunun yerel minimum
ve yerel maksimum noktalarının ordinatlarının top-
lamı kaçtır?
A)-5
X
E) 3
Kafa Dengi
Lise Matematik
Ekstremum NoktalarBİ
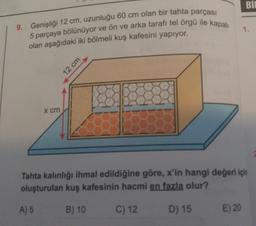
9. Genişliği 12 cm, uzunluğu 60 cm olan bir tahta parçası
5 parçaya bölünüyor ve ön ve arka tarafı tel örgü ile kapalı
olan aşağıdaki iki bölmeli kuş kafesini yapıyor.
1.
X cm
Tahta kalınlığı ihmal edildiğine göre, x'in hangi değeri için
oluşturulan kuş kafesinin hacmi en fazla olur?
A) 5
B) 10
C) 12
D) 15
E) 20
12 cm

Lise Matematik
Ekstremum NoktalarA)
C)
0
-26
23
13-1,9-26
(1,9)2-2-1,9+1
13-2,2-26
(2,2)²-2-2,2+1
E)
Yanda y=
eğrisi verilmiştir.
Buna göre, aşağı-
daki işlemlerden
hangisinin sonucu
en büyüktür?
B)
xxx
13x-26
x²-2x+1
13-2,1-26
(2,1)2-2-2,1+1
13-3,1-26
(3,1)2-2-3,1+1
13-3,2-26
(3.2) ²-2-3,2+1

Lise Matematik
Ekstremum Noktalardaiy=-x-4
RO
4
da
Şekilde grafik, f(x) = ax² + bx + ye
aittir. d, doğrusu parabole (-4, 0) nok-
tasında teğet ve d, 1. d₂ dir.
1
Verilenlere göre, a b çarpımı
kaçtır?
106
4
a(6-1)x-83
(6-1) 3201-0
3
(-:-)
f(0) 1(1
nucu k
![lığın-
dir?
+4
efa
e
ki
32-8
$-3
11.
261-12
72
8
T
-3-2
-1
-3
2
B)-3 C) -2
T
-4
2
3 4
Yukarıdaki şekilde grafiği verilen ve [-4, 4] aralığın-
da tanımlı olan f(x) fonksiyonunun yerel minimum
ve yerel maksimum noktalarının ordinatlarının top-
lamı kaçtır?
A) -5
y = f(x)
D) 2
E) 3
Kafa Dengi](https://media.kunduz.com/media/question/seo/raw/20230214192314025062-4736609.jpg?w=256)
Lise Matematik
Ekstremum Noktalarlığın-
dir?
+4
efa
e
ki
32-8
$-3
11.
261-12
72
8
T
-3-2
-1
-3
2
B)-3 C) -2
T
-4
2
3 4
Yukarıdaki şekilde grafiği verilen ve [-4, 4] aralığın-
da tanımlı olan f(x) fonksiyonunun yerel minimum
ve yerel maksimum noktalarının ordinatlarının top-
lamı kaçtır?
A) -5
y = f(x)
D) 2
E) 3
Kafa Dengi
![rafiği
e
)
polimal
16. Aşağıda y =
verilmiştir.
-8
f(x) ve y = g(x) fonksiyonlarının grafikleri
y
-4-3 O 2
D) (-3, 0]
y = f(x)
B) (5, 7]
9
f(x) fonksiyonunun azalan olduğu en geniş küme
A, g(x) fonksiyonunun artan olduğu en geniş küme
B olduğuna göre, A - B kümesi aşağıdakilerden han-
gisidir?
A) (0,5)
E) (-4,-3)
-X
y = g(x)
C) (0, 2]](https://media.kunduz.com/media/question/seo/raw/20230214081513317781-4747276.jpeg?w=256)
Lise Matematik
Ekstremum Noktalarrafiği
e
)
polimal
16. Aşağıda y =
verilmiştir.
-8
f(x) ve y = g(x) fonksiyonlarının grafikleri
y
-4-3 O 2
D) (-3, 0]
y = f(x)
B) (5, 7]
9
f(x) fonksiyonunun azalan olduğu en geniş küme
A, g(x) fonksiyonunun artan olduğu en geniş küme
B olduğuna göre, A - B kümesi aşağıdakilerden han-
gisidir?
A) (0,5)
E) (-4,-3)
-X
y = g(x)
C) (0, 2]
Lise Matematik
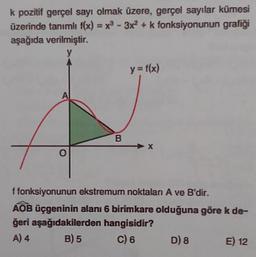
Ekstremum Noktalark pozitif gerçel sayı olmak üzere, gerçel sayılar kümesi
üzerinde tanımlı f(x)=x²-3x2 + k fonksiyonunun grafiği
aşağıda verilmiştir.
V
0
y = f(x)
X
f fonksiyonunun ekstremum noktalan A ve B'dir.
AOB üçgeninin alanı 6 birimkare olduğuna göre k de-
ğeri aşağıdakilerden hangisidir?
A) 4
B) 5
C) 6
D) 8
E) 12
