Ekstremum Noktalar Soruları

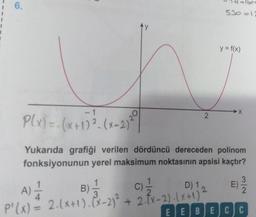
6. P(x) = (x+1) ². (x-2) 1 ₂0 D) 1 2 A) 1/14 B) -1/14 C) 3 P'(X) = 2-(x+1). (x-2)² + 2(x-2)(x+1) 530=12 Yukarıda grafiği verilen dördüncü dereceden polinom fonksiyonunun yerel maksimum noktasının apsisi kaçtır? 2 y = f(x) X E) 3 2 EE BECC

10. Şekilde gerçel sayılarda tanımlı y = f(x) parabolü verilmiştir. ● x in {0, 1, 2, 3} değerleri için; If(x)| fonksiyonu a farklı, f(lxl) fonksiyonu b farklı, √f(x) fonksiyonu ç farklı ● ● y % - A) a<b<c B) a <c<b D) a = b = c y = f(x) x değerinde türevli olduğuna göre aşağıdakilerden hangisi doğrudur? 3 X C) c<a<b E) a = c < b

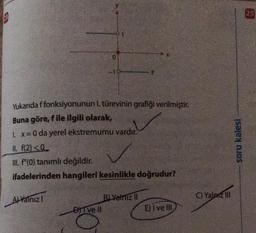
13 Yukarıda f fonksiyonunun 1. türevinin grafiği verilmiştir. Buna göre, f ile ilgili olarak, 1. x = 0 da yerel ekstremumu vardır. II. f(2)<0 III. f"(0) tanımlı değildir. ifadelerinden hangileri kesinlikle doğrudur? A) Yalnız I 0 DITVE II B) Yalnız II E) I ve III C) Yalniz III soru kalesi 25

MATEMATIK VA 8. • f(x) = (x²-1 ● X, [x²-1, x<0 flx) · g(x) = (x³²-1 -x³-1, ise x ≥ 0 ise x³, x>0 ise x≤0 ise id uğublo h(x) = |x-1| A) Yalnız f municy nigi teie smu biçiminde tanımlı f, g ve h fonksiyonlarından hangileri nin yerel ekstremum noktası yoktur? id Boxinley B) Yalnız g C) f ve g Mubin D) f ve he hell E) g ve hahelebell Isanley (A ifadeler 2. A) Yalr Ge e

4 NA -3 -2 -1 0/1 2 3 Yukarıda f(x) fonksiyonunun türevinin grafiği verilmiştir. Buna göre, aşağıdakilerden hangisi doğ- rudur? ✓ (-∞, -2] için f(x) azalandır. Exf(4)<fx f'(x) XULA Af(0) <0 J B) f(2)=0 D) f"(5) <0

25 =1(x) = 3ax²¹² +2bx4c 39(x+4) (x-2) 17 f(x) 3. dereceden bir fonksiyondur. f(x) = ax³ + bx² + cx + d, ● f(-4)= 2 ve f'(-4)= 0 f(2)=-2 ve f'(2) = 0 olmak üzere 167 I. f(x) fonksiyonu birbirinden farklı 3 noktada x - ekseni- ni keser. mibe II. f(x) = 2 denkleminin 2 tane çözümü vardır. III. f(x) = -3 denkleminin 1 tane çözümü vardır. A) 1 B) 2 masti IV. A(-1,0) noktası f(x) fonksiyonun dönüm noktasıdır. V. (-4, 2) aralığında f(x) fonksiyonun azalandır. ifadelerin kaç tanesi daima doğrudur? 2 C) 3 D)4 0-10 /E) 5

YKS/Temel Matematik 22. 3. y 201 -3 # -2 Şekilde f'(x) grafiği verilmiştir. 1. (-∞, -3) aralığında f(x) azalan 2. (0, ∞) aralığında f(x) artan 3. f'(x) eğrisi (-3, 0) aralığında azalandır. 4. f(x) eğrisi (0, ∞) aralığında konvekstir. A) 5. f(x) eğrisinin (-∞, 1) aralığında 2 tane dönüm noktası ginga 21 vardır. Yukarıdaki ifadelerin kaç tanesi doğrudur? B) 2 V f'(x) C) 3 + IS D)4 E) 5 24. yayıncılık DWWD 9 2

6. f(x) = x² - a x+1 X₁=x2-2 larının apsisleri x₁ ve x₂ dir. fonksiyonunun ekstremum nokta- x₁ - x₂ = -2 olduğuna göre, a kaçtır? TOLL 2x (x+¹) - (x²_a) (1) (X+1) ² MMA 2x² + 2x -x ² +a x²+2x+9=0O x²+2x+1

6. Aşağıda f fonksiyonunun türevi olan f' fonksiyonunun gra- fiği verilmiştir. -3 xxx Buna göre, 0 Ay 2 D) I ve III -3 # ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II X fonksiyonunun yerel maksimum noktası yoktur. II. f fonksiyonunun x = -3 apsisli noktada yerel minimu- mu vardır. 2 # III. f' fonksiyonunun yerel ekstremum noktalarının apsis- Teri toplamı -1'dir. C) I ve II E) I, II ve III +

1. Buna göre, RESTPROMOC YA 4 II. III. 2 1 0 Şekilde f fonksiyonunan [05] aralığındaki grafiği veril- miştir. A) Yalnız I N HAN 3 I. f fonksiyonunun [0, 5] aralığında mutlak maksimum değeri yoktur. 5 f nin mutlak minimum değeri 0 dir. COMPO REA D) I ve III X f nin x=3 teki yerel minimum değeri 1 dir. METSMED ifadelerinden hangileri doğrudur? B) Yalnız II C) I ve II JE) I, II ve IIL U

23. Baş katsayısı 1 olan üçüncü dereceden bir P(x) polinomu için, XX-2=0 X-4=0 P(2) = P(4) = 0 olduğu bilinmektedir. P(x) polinomunun x = 1 apsisli noktasında bir yerel maksimumu olduğuna göre, P(x) polinomunun (x - 6) ile bölümünden kalan kaçtır? C) 35 A) 23 B) 28 D) 46 E) 52

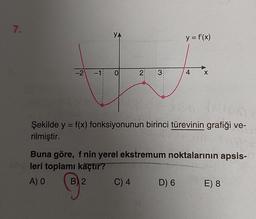
7. YA H -2 -18 0 2 3 C) 4 y = f'(x) PO Şekilde y = f(x) fonksiyonunun birinci türevinin grafiği ve- rilmiştir. 4 X Buna göre, f nin yerel ekstremum noktalarının apsis- leri toplamı kaçtır? A) O B) 2 D) 6 E) 8

11. DENEME 21. f(x) = 2x³+(k-1)x²+7x-3 eğrisinin x eksenine paralel olan teğetlerin değme noktalarının apsisleri toplamı 6 oldu- ğuna göre k'nın değeri kaçtır? A)-17 B)-13 C) -7 D) 7 E) 17 23. AY 6 3 Şek

(D) AY -1 631 f(x) a b Yukanda f(x) in (a, b) aralığındaki grafiği verilmiştir. > fix) >0 fix) LO X>0 Buna göre, aşağıdaki fonksiyonlardan hangisi (a, b) aralığında artandır? + 1x²). 2X 4 A) 3.f(x) BH(X) C) f(x) - x² 1 f(x) -X f(x) E)

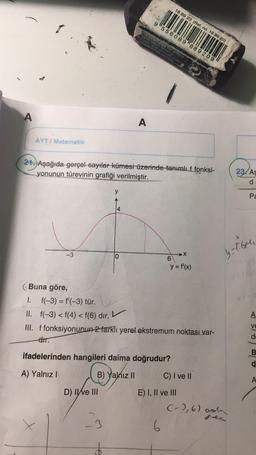
A AYT/ Matematik -3 Buna göre, y D) II ve III 4 -3 10 OPE 21. Aşağıda gerçel sayılar kümesi üzerinde tanımlıf fonksi- yonunun türevinin grafiği verilmiştir. Calle Orte vor added brand 7 9 556089 889209 A cklead penerasin mooth 18 89 23 (Ref. no. 18 89 20) 6 ifadelerinden hangileri daima doğrudur? A) Yalnız I B) Yalnız II I. f(-3) = f'(-3) tür. II. f(-3) <f(4) < f(6) dır. III. f fonksiyonunun 2 farklı yerel ekstremum noktası var- dir. y = f'(x) X E) I, II ve III C) I ve II 23/As (-), 6) ada Fe y=tben Pa T A Ve de B d A

um de- E) 48 10. f(x) = x³ - ax² + 3x -1 fonksiyonunun ekstremum noktası olmadığına göre, a'nın en geniş değer aralığı aşağıdakilerden hangisi- dir? A) (0, 1] 1-E 2-E D) (-∞, 2] 3-B B) [-2, 0) 4-D 5-C C)[-3, 3] E) [-9, 1] 6-B 7-A 8-A Buna göre, 1. fonks 11.(6, 7) mu v H (3, 2 varc bilgilerin A) Yaln 9-C 10-