Ekstremum Noktalar Soruları

Lise Matematik
Ekstremum Noktalar10. y = f(x) fonksiyonu her x E R için türevli bir fonksi-
yondur.
f'(x) = 0 denkleminin çözüm kümesi (-2, 0, 4} dür.
f'(-3) > 0
f¹(-1) < 0
f¹ (3) > 0
f'(5) > 0 olduğuna göre,
f fonksiyonunun yerel minimum noktasının apsisi
kaçtır?
obati

Lise Matematik
Ekstremum Noktalarr =
2.
tüğüne göre, okun atıldıktan 2 saniye sonra yerden
yüksekliği kaç metredir?
B) 6
A) 4
C) 7,5
f(x)=-x²+8x+2
D) 8
E) 10
fonksiyonunun azalan olduğu aralık aşağıdakilerden
hangisidir?
sekliğ
Şekil
nokt
rab
ola
ha
E
A) (4, ∞0) B) (2, ∞0) C) (-∞0, 4) D) (-4,4) E) (0, ∞) eis
Yayınlanı
Lise Matematik
Ekstremum Noktalar5.
BENIM
-5
fun
-2
AY
D) II ve III
T-MA
by = f(x)
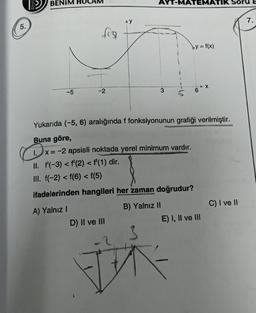
Yukarıda (-5, 6) aralığında f fonksiyonunun grafiği verilmiştir.
Buna göre,
mata
1.x
1.x = -2 apsisli noktada yerel minimum vardır.
II. f'(-3) < f'(2) < f'(1) dir.
III. f(-2) < f(6) < f(5)
ifadelerinden hangileri her zaman doğrudur?
A) Yalnız I
B) Yalnız II
D
TIK S
E) I, II ve III
C) I ve II
7.

Lise Matematik
Ekstremum NoktalarÇAP / AYT
24. Dik koordinat düzleminde f(x) = √Ixl fonksiyonun gra-
fiği verilmiştir.
Buna göre,
f'(-3) >0
L. f(x) fonksiyonunun ekstremum noktası yoktur.
III. a < b <0 olduğunda f'(a) > f'(b)'dir.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
y=vlxl
DI vell
C) Yalnız III
E) II ve III

Lise Matematik
Ekstremum Noktalar10. f(x) = x³ - 6x² + 4x + 5
fonksiyonunun yerel minimum ve yerel maksimum nok-
talarının apsisleri toplamı kaçtır?
A) -4
B)-2
C) 4
f(x1=3x²-12x +4
3x
x
D) 6
E) 12
%
bu
164-G₁3.4=144-66
VA 34 ***** 36 *****

Lise Matematik
Ekstremum Noktalar9.
*(x) = x² + ax² + bx - 2
f(x)=
3
fonksiyonu sadece (1, 5) aralığında azalan olduğuna göre
a + b toplamı kaçtır?
A) -3
B)-1
C) 1
D) 2 E) 3
201
Lasquaficli ugon &
12. f(x) = x³ +:
fonksiyonunu
kaçtır?
A) 7
B)
3x
Lise Matematik
Ekstremum Noktalarktasın-
göre, a
K
-24
+ 1
4 + (-11-3)
(+-4/(x+1)
Xo = 4 to==+
6. f(x) = x³-ax² + 3x + b eğrisi x = -1 apsisli nok-
tasında y = 1 doğrusuna teğet olduğuna göre,
a.b çarpımı kaçtır?
2
*(x=3x² 29X+3
4²2) = 3 + 2a +5
6+29 = 1
-3
9= 2/1/2
1. y = 2x + 1 2. (2, 1) 3. 3 4. 1 5.3 6.-6
9
(₁
(01
4.
Yu
siy
nu
g
k
glix=
Lise Matematik
Ekstremum NoktalarA
Şekilde
y = f(x) fonksiyonunun
grafiği verilmiştir.
Buna göre y = f(x) aşağıdakilerden hangisi olabi-
lir?
A) y = 2x³ + 3x + 12
B) y = 2x³ - 3x + 12
C) y = 2x³ + 3x2 - 12x
D) y = 2x³ +9x
E) y = 2x³ 3x2 - 12x

Lise Matematik
Ekstremum NoktalarSORULAR
= f'(x)
un gra-
erden
GÜRAY KÜÇÜK YAYINCILIK
GURAY KÜÇÜK YAYINCILIK
Vygulamalar
3. Matematik öğretmeni Gamze Hanım, sınıftaki öğrend
lere aşağıdaki soruyu sormuştur.
24
Eray
Bu soruya sınıftaki Ali, Eray ve Turgay adlı öğrenciler
aşağıdaki cevapları vermişlerdir.
Turgay
Türev ve
ALA
Gerçel sayılarda tanımlı
"f(x) = 6x³-12x³
eğrisinin kaç farklı yerel
ekstremum noktası vardır?"
"f(x) in derecesi 5 olduğundan 5 tane
ekstremumu vardır."
"f(x) in birinci türevini alıp sıfıra eşitledim.
x = 0 noktası çift katlı olduğundan ekstre-
mum nokta olmaz. f nin iki tane ekstre-
mumu vardır."
"f(x) in birinci türevini alıp sıfıra eşitledim.
4 tane ekstremumu vardır."
Buna göre, hangi öğrenci soruya doğru cevap ver-
miştir?
B) Eray
C) Turgay
D) Ali ve Eray E) Eray ve Turgay
2
2
6x²/5x²-6/5x²=6
X=0 (4₁2) X = 6 x=
3
G
30x4-36x
30-0
ep-a
4-
Maks
(C
Izlenecek
1. Sorud
2. 1. der
3. Çekil
tek d
4. Bu c
nun
Ta
et

Lise Matematik
Ekstremum Noktalara #0 olmak üzere, y = ax³ + bx2 + cx+ d fonksi-
yonu ile ilgili olarak,
V. Büküm (Dönüm) noktası vardır.
II. Yerel minimum noktası vardır.
Ili. Yerek maksimum noktası vardır.
Yargılarından hangisi doğrudur?
A) Yalnız I
B) Yalnız II
D) I ve II
C) Yalnız III
E) II ve III

Lise Matematik
Ekstremum Noktalar13.
y=
3
+²
2
parabolünün x = 1 apsisli noktasından çizilen teğetin
üzerinde değme noktasından itibaren 10 br uzun-
luktaki B ve C noktaları alınıyor.
y
B ve C noktalarının ordinatları farkı kaç br dir?
A) 10 B) 8
C) 6
D) 4
E) 3

Lise Matematik
Ekstremum Noktalarww.aydinyayinlari.com.tr
ÖRNEK 8
(x)=x²-7x olduğuna göre, y = f'(x) fonksiyo-
unun eşitini bulunuz.
TÜREV ALMA-2
2108
26.
27.
21108
ttttt till t t t t t
YAYINLARI
Gerçek sayılar kümesi üzerinde tanımlı f fonksiyonu
f(x) = |x|-2|
kuralı ile verilmiştir.
Buna göre, f fonksiyonunun türevsiz olduğu nokta-
ların apsisleri çarpımı kaçtır?
A) -4
C) 2
B) 0
LİMİT VE TÜRE
D) 4
fec
a, b, c ve d E R
X
xl
da türevlenebilir.
SONUÇ
E)-2
Barış
YAYINLARI
y = f(x) fonksiyonu her noktada türevlenebilir
ise polinom fonksiyonudur.
II. y = f(x)| fonksiyonu köklerinde türevlenemez.
III. f(x)=- fonksiyonu sürekli olduğu her nokta-
29.

Lise Matematik
Ekstremum Noktalar22.) a, b ve c gerçel sayılar olmak üzere,
4
X
f(x) = 4
3
+ ax³ + bx² + cx+2
fonksiyonunun
• sadece x = -1 apsisli noktada yerel ekstremumu
vardır.
• f'(-2) = 0'dır.
Jax²+ 16x+c +x³
Buna göre, f(-1) kaçtır? 129-utc-8=0
A) +
B) =
3
5
C)/20/07/20
D)
E)
12
129-46+C-1=0 86²-26 +Cc+1=0
129-46+21
</20-2b+5=1
AL + +x² + x² +
![7. y = f(x) fonksiyonunun grafiğine x = a apsisli noktada
teğet olan doğru aşağıda verilmiştir.
D)
y
f'(a)
f(a)
A
B) f(a)
CO
a
Buna göre, doğru üzerindeki [AB]'nin x ekseni
üzerindeki dik izdüşümünün uzunluğu aşağıdaki-
lerden hangisidir?
A) f(a)
y = f(x)
B
f(a)
f(a)
C)--
E)-f(a) f(a)](https://media.kunduz.com/media/question/seo/raw/20230201165216970628-3001969.jpg?w=256)
Lise Matematik
Ekstremum Noktalar7. y = f(x) fonksiyonunun grafiğine x = a apsisli noktada
teğet olan doğru aşağıda verilmiştir.
D)
y
f'(a)
f(a)
A
B) f(a)
CO
a
Buna göre, doğru üzerindeki [AB]'nin x ekseni
üzerindeki dik izdüşümünün uzunluğu aşağıdaki-
lerden hangisidir?
A) f(a)
y = f(x)
B
f(a)
f(a)
C)--
E)-f(a) f(a)
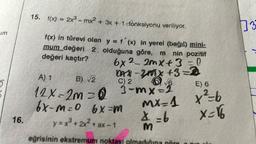
Lise Matematik
Ekstremum Noktalarim
16.
15. f(x) = 2x³ - mx² + 3x + 1-fonksiyonu veriliyor.
f(x) in türevi olan y = f(x) in yerel (bağıl) mini-
mum değeri 2 olduğuna göre, m nin pozitif
değeri kaçtır?
6x22mx+3=0
DAX-2001X +3=2
Dar-2008
C)
A) 1
B) √2
12 X-2m = Q 3-mx-2
6x-m=0 6x-m
y=x²+2x²+ax-1
eğrisinin ekstremum noktası
E) 6
MX=1 x ²²=b
x=16
9= X
34
3
Lise Matematik
Ekstremum Noktalar(2,7)
3
150 god. (x² + x Fly). (3x² + (200 + x P)
f(x)
18
10) f(x) = x³ + 3x² +2²4
B2
fonksiyonunun yerel maksimum değeri 11 olduğuna
göre, m kaçtır?
B) 6
2
füres=9
2ax+b
atb-g
19+26-2
A) 5
³+2x²). (3x²+4x)+1
5
C) 9
D) 10
E) 11
