Faktöriyel Soruları

Lise Matematik
Faktöriyel30 kişilik bir sinifta 18 tane kız öğrenci vardır. Erkek-
lerin 3 tanesi, sınıfın ise %40'ı çalışkandır.
Buna göre sınıftan rastgele seçilen üç kişinin,
üçünün de çalışkan olduğu bilindiğine göre sa-
dece birinin kız olma olasılığı kaçtır?
13
7
27
A)
B)
C)
10
55
220
1
3
D)
E)
5
10

Lise Matematik
Faktöriyel10. Bir torbada eşit büyüklükte 4 mavi, 2 beyaz ve 3
bilye vardır.
Torbadan rastgele çekilen iki bilyeden yalnız birinin
mavi olduğu bilindiğine göre, diğerinin beyaz gelme
olasılığı kaçtır?
3
E)
9
10
2
B)
A
5
A)

Lise Matematik
Faktöriyelbry yayınları
60 140
12. Bir parktaki iki tane 3 kişilik farklı banka 3 kız ve 3 erkek
öğrenci oturacaktır.
Bu 6 öğrenci her bankta en az bir kız öğrenci bulun-
mak şartıyla kaç farklı şekilde banklara oturabilirler?
A) 440 B) 548
C) 624 D) 648
E) 684
1. bank
2. bank

Lise Matematik
Faktöriyel1.
Bir davete katılan Ayça, Büşra, Ceyda, Deniz, Erdem
ve Furkan isimli altı arkadaş için etrafında 6 sandalye
bulunan şekilde gösterilen üzeri desenli bir masa ayrıl-
mıştır.
000
Araları bozuk olan Ayça ve Büşra, bu masadaki yan
yana olan sandalyelere de karşı karşıya olan sandalye-
lere de oturmak istememektedirler.
Buna göre, bu altı arkadaş masa etrafındaki bu
sandalyelere kaç farklı şekilde oturabilirler?
A) 432
B) 384 C) 360
D) 288
E) 240
3. Bi
sa
ç
ayınları
h

Lise Matematik
Faktöriyelde Temel Kavramlar ve Kirişin Özellikleri
O₁ ve 0₂
4.
çemberlerin
merkezi
A
X B
02
10₁0₂l = 16 cm
Yukarıdaki şekilde; çemberlerin birbirine göre en uz
iki noktası arasındaki uzaklık 39 cm olduğuna gör
IABI= x kaç cm'dir?
CO
7.
Yazılıy
Yuka

Lise Matematik
Faktöriyel7.
A ve B birer doğal sayı, 3A288 beş basamaklı bir sayıdır.
10!=3A288.10B
olduğuna göre, A+B toplamı kaçtır?
ob A) 6
C) 8
D) 10
E) 12
B) 7
blo
Aşağıdaki tabloda bir züccaciyede bir günde satılan ürün-
lerin fiyatları
, satış adetleri ve satış tutarları verilmiştir.

Lise Matematik
Faktöriyel185
x'e
12. a ve b pozitif tam sayılar olmak üzere,
247
EKOK (a!, b!) = b!
Bu
18
EBOB (a!, b!) = a!
21
EKOK(a!,b!)
EBOB(a!,b!)
= 120
2.
E
e III
olduğuna göre, a + b toplamı en az kaçtır?
r
A) 1
B) 5
C) 6
D) 20
E) 36
108

Lise Matematik
FaktöriyelA) 390
B) 411
12. Aşağıdaki tabloda Burak ile Nezaket'in kendileri-
ne özel bir simit yapma süresi ve bu sürede kaçar
adet simit yaptığı verilmiştir.
c/
C
Süre (dk)
Adet
Burak
2
1
Nezaket
3
4
Burak'ın bir simitte kullandığı un miktarının 3 katı,
Nezaket'in bir simitte kullandığı un miktarının 5 ka-
tina eşittir.
10 saat sonunda ikisi toplam 39 kg un kullanmıştır.
YAYIN DENİZİ
Buna göre, Nezaket bir simitte kaç kg un kul-
lanmıştır?
B) 0,02
A) 0,01
D) 0,04
C) 0,03
E) 0,06
6

Lise Matematik
FaktöriyelTIK TESTİ
19
Elul
adet
adet adet adet adet
Üstteki 20 çubukta 1'den 20 ye kadar olan sayıda
boncuklar takılıdır. Bu boncuklar aşağıdaki boş çu-
buklara karışık olarak fakat her çubuktaki boncukla-
rin
tamamı farklı bir çubuğa aktarılacaktır.
Bu şekilde yapılacak aktarma sayısı A=k.28.36.50
dir.
k, a, b, c pozitif tam sayılar olduğuna göre,
a+b+c en çok kaçtır?
A) 25
B) 27
C) 28
D) 29
E) 30

Lise Matematik
Faktöriyel15. Aşağıdaki 9 askılıktan üçüne iki kırmızı ve bir beyaz olmak
üzere 3 farklı şemsiye yerleştirilmiş durumdadır. Kalan 6
boş askılığa ikisi kırmızı ve biri beyaz olmak üzere 3 farklı
şemsiye, her bir yere 1 şemsiye gelecek şekilde
asılacaktır.
2K IB
As(
0
1.2
Bu işlem rastgele yapıldığında kırmızı şemsiyelerden
herhangi ikisinin yan yana duran askılıklarda olmama
ve beyaz şemsiyelerin yan yana olmama olasılığı
kaçtır?
delib yoynimals meve SEESSA
250 g slysa la bibimised nollbo
1
1
1
1
B)
C)
D)
15
10
30
20
08
0
BO 8678
Po
E)
A)
-10
13.A 14.C 15.E
Uc!
Bes

Lise Matematik
FaktöriyelBir davete katılan Ayça, Büşra, Ceyda, Deniz,
Erdem ve Furkan isimli alti arkadaş için etrafın-
da 6 sandalye bulunan şekilde gösterilen üzeri
desenli bir masa ayrılmıştır.
VY
O
Araları bozuk olan Ayça ve Büşra, bu masadaki
yan yana olan sandalyelere de karşı karşıya olan
sandalyelere de oturmak istememektedirler.
Buna göre, bu altı arkadaş masa etrafındaki bu
sandalyelere kaç farklı şekilde oturabilirler?
A) 432 B) 384 C) 360 D) 288
C D)
E) 240

Lise Matematik
Faktöriyel13. 1 den x'e kadar olan x tane sayının kareleri
toplamı A = 12 + 22 + 32 + .... +x? olduğuna göre,
her terimin tabanı 1 arttırıldığında A ne kadar
artar?
x(x + 1)
AX
C)
2
D) x(x - 1) E) x² + 2x
B) x2

Lise Matematik
FaktöriyelORI
6.
Şarj Doluluk
Yüzdesi (x)
Maksimum Hız
Birim Zamanda
Tüketilen Şarj
Yüzdesi
0<x< 25
10 km/sa
a
Hralar-
nme-
15 km/sa
2a
25 < x < 50
50 < x < 75
75<x100
4a
20 km/sa
30 km/sa
8a
att 6
mütlü
ba
eği
ne
Yukarıda verilen tabloda bir elektrikli motosikletin şarj yüz-
desi, maksimum hızı ve birim zamanda tükettiği enerji mik-
tarı arasındaki ilişki verilmiştir. Bu motosikletin şarj durumu
%90 iken %50 olana kadar 29 km yol gidebilmiştir.
Buna göre, şarj durumu %40 olan bir motosiklet en
fazla kaç km yol gidebilir?
A) 50
B) 54
D) 64 E) 68
C) 58

Lise Matematik
Faktöriyel420
Buna göre, A ve B şehirleri arasi kay
A) 340 B) 360
- otomobil
40km - kom you
C) 380
D) 400
->
3,5
30.3.3
8. Bir hareketli bir yolun á sını ortalama 50 km/sa hızla, ka-
lan yolun % 60 ini ortalama 75 km/sa hızla, geri kalan yolu
da ortalama 100 km/sa hızla giderek yolculuğunu 14 saatte
tamamlıyor.
Buna göre, yolun tamamı kaç km dir?
A) 950
B) 1000
C) 1050
D) 1100
E) 1150
9. Yol (km)
A
RU BANKASI
Yanda verilen grafik A ve
B araçlarının aldıkları yol-
ların zamana göre değişi-
mini göstermektedir.
300
1
B
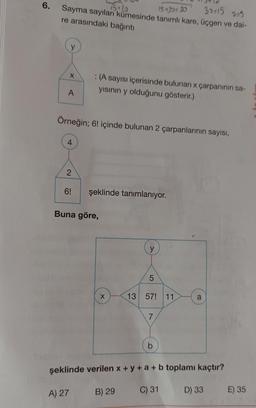
Lise Matematik
Faktöriyel6.
38:15 225
1510
Sayma sayıları kümesinde tanımlı kare, üçgen ve dai-
re arasındaki bağıntı
15430:30
y
X
: (A sayısı içerisinde bulunan x çarpanının sa-
yısının y olduğunu gösterir.)
A
Örneğin; 6! içinde bulunan 2 çarpanlarının sayısı,
4
2
6!
şeklinde tanımlanıyor.
Buna göre,
y
5
X
13 57! 11
a
7
b
şeklinde verilen x + y + a + b toplamı kaçtır?
A) 27
B) 29
C) 31
D) 33
E) 35

Lise Matematik
Faktöriyel19. Bir davete katılan Ayça, Büşra, Ceyda, Deniz, Er-
dem ve Furkan isimli altı arkadaş için etrafında 6
sandalye bulunan şekilde gösterilen üzeri desenli
bir masa ayrılmıştır.
K
JOD
Araları bozuk olan Ayça ve Büşra, bu masadaki yan
yana olan sandalyelere de karşı karşıya olan san-
dalyelere de oturmak istememektedirler.
Buna göre, bu altı arkadaş masa etrafındaki bu
sandalyelere kaç farklı şekilde oturabilirler?
A
A) 432
B) 384
C) 360
D) 288
E) 240
ly
61 3.2.41 4.2.41)
1
N.
L 720
24
24
4 298
7
B
lou
192
Y
x 6
1 432
iskor
