Köklü İfadelerde İşlemler Soruları

larını cep saniyenin E) 122 10 10 ed 910g snua 14. Toplama, çıkarma, çarpma ve bölme işlemi sembolleri- nin her biri aşağıda belirtilen dairelerin içerisine yazıla- sta/8 80 8 caktır. 1. II. √24√6 bir rasyonel sayıdır. 4 9 III. 40 88.813 bir doğal sayıdır. bir doğal sayıdır. A) ÷, X, +, - A8,8 (3 2 4 IV. 16 bir doğal sayı değildir. sonlayne met Het D) ÷, +, X, - thivee cast id x . T (al mis) (8-x Yukarıda verilen bilgilere göre, I, II, III ve IV numara- daki dairelerin içine sırası ile aşağıdakilerden hangi- leri yazılmalıdır? B) +, X, +, - op arbe C) +, +, X, - E) +, -, X, +

Art. No. 88/384006381493185 8. Test . .N B) 6 ny. yilver 1. Z tam sayılar kümesi olmak üzere, M=|-73,41 N=[√3,2¹] kapalı aralıkları için (M U N) n Z kümesinin eleman sayısı kaçtır? A) 7 C) 5 D) 4 Faber-Castell AG Weagerecht lagers Made in Austra Universi E) 3 1 4.

10. x, YER olmak üzere, I. √x² = |x| 2 26 - 29 -4 272 5-45-875-4.1 X yukarıda verilen eşitliklerden kaç tanesi daima doğrudur? A) t X II. II. X X X √ XIII. √x.y = √x - √y X IV. (√x)² = x B) 2 C) 3 D) 4 -2 E) Hiçbiri

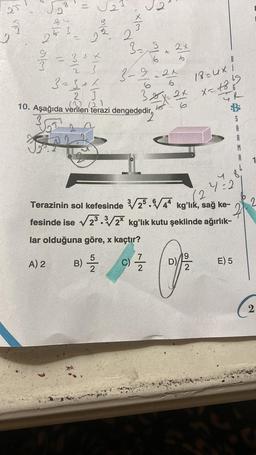
5 Cale 8 2 - J2 aler 2 x/m 2 3₂2 2x 6 ¾/7 = 3+ * 3 23 323+1 2 3 10. Aşağıda verilen terazi dengededir, A 6 3-9-24 6 C) 6 xx 2x 19 B 7 30/12/2 18=4×1 x=1819 12 Terazinin sol kefesinde √25.44 kg'lık, sağ ke- fesinde ise √23.3√/2 kg'lık kutu şeklinde ağırlık- lar olduğuna göre, x kaçtır? A) 2 B) -5/2 A 4 8. 4=2 E) 5 2 2

-10 2 bun 2422/19 3 A) 8 y = ax² B) jalm IOAI = IOBI, T teğet değme noktasıdır. 3 8 nin alanı kaç 5 O AC 8 T Taralı alan birimkare olduğuna göre, ATC üçgeni- birimkaredir? C) ^ 78 9:1 ➤X D) 1 9.4²-kab 94²44570 E) CAP 9 4. 167

3. 4. √(-4)²+(-6)* -√(-5)³ (-~) işleminin sonucu kaçtır? A) 5 B) 7 3+ (4) (3) C) 10 12 ==1==1 12 - 1 1 √√/=+=+=+=+=+=+16=√ √ +=+=+=+=+ ● 9 16 D) 12 işleminin sonucu kaçtır? A) B) C) 1 6 A D) *6 1 E) 15- 12 2 17/0 G S 1e1 12 R A

2. <-- A) 4 a ve b pozitif reel sayılardır. a³ = b² = 129 11- olduğuna göre, a ile b arasında kaç tam sayı vardır? B) 5 16/ 2023 216 5-125 63=216 FEN BİLİMLERİ YAYINLARI C) 6 |u2|= (L D) 7 82,8,8.15 E) 8 www.fenbili EĞİTİM CİDDİ KUF

13 2 2√3 15. 2ab sayısı, üç basamaklı bir doğal sayıdır. √2ab cm B6 3 Yukarıdaki dikdörtgenin kenar uzunlukları √72 cm ve √2ab cm olup dikdörtgenin alanı santimetrekare cin- sinden bir doğal sayıdır. Buna göre a + b nin alabileceği en büyük değeri, a + b nin alabileceği en küçük değerden kaç faz- ladır? A) 6 B) 10 √72 cm C) 14 D) 16

1. Aşağıda X ve X işlemleri tanımlanmıştır. X(a): a'nın √b fazlası X(a): a'nın √b eksiği Yeni Nesil Sorular b bir pozitif tam sayı olmak üzere, X(4). X(4)=7 olduğuna göre, b kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9

13. TYT/ Temel Matematik 1 √a+√a+1 şeklinde tanımlanıyor. a-rat Buna göre, a 1 2 + 3 + ... + 8 toplamının sonucu kaçtır? A) -2 B)-1 C) 1 +1/2+1/ 8- 12+13 D) 2 E) 3 L 13+14 2+12+12+13+√3+√uth +55+/6+12+1² 16-2 15. Güne katıl 3 21 216

................/20....... A D K N Soru Say 8 Doğru Says Yanlış Sayısı OOO D) √15 M E) 2√5 B ABCD ve KLMN birer dikdörtgen olmak üzere, ABCD dikdörtgeninin üzerine, boyutları √245 cm ve √405 cm olan bir fotoğraf yerleştirilmiştir. Pozitif tan sayılar kümesinde, 485 ABCD dikdörtgeninin alanı 495 cm2 ve fotoğrafın kenarlarının fon kenarlarına uzaklığı (x) eşit olduğuna göre, x değeri kaç santimetredir? A) √2 B) √5 C) √10 C

-5 KAS Bir dikdörtgenler prizmasının hacmi üç ayrıtının çarpılmasıyla bulunur. Aşağıda iki farklı dikdörtgenler prizması verilmiştir. √80 √5 √8 √2 2 VIT √3 2-√33 Bu prizmaların üzerinde yazan ölçüler metre türündedir ve her iki prizmaya metreküp türünden tam sayı olan miktarlarda su doldurulacaktır. Buna göre, iki prizmaya da doldurulan su miktarları en çok olduğunda mavi prizmadaki su miktarı, yeşil prizmadaki su miktarından kaç metreküp fazla olur? A) 1 (B)2 (64) 550 (187 D) 40 25 (√33 (36 10-8-2 E) 5 97

15. Num Lock Hote 7 C C 4 1 www 0 8 5 2 9 6 3 Yukarıdaki şekilde bir bilgisayar klavyesinin, rakamların yazılı olduğu dikdörtgen biçimindeki bölümü gösterilmiştir. Küçük tuşların her biri kenar uzunluğu 1,1 cm olan eş ka- relerden oluşmaktadır. Ayrıca, komşu iki tuşun birbirine en yakın olan kenarları arasında 0,2 cm den daha az boşluk bulunmaktadır. Buna göre, "Num Lock" yazan tuş ile "0" rakamının yazılı olduğu tuş arasındaki en kısa mesafe santimetre türünden aşağıdakilerden hangisi olabilir? A) TO 15 C) √17 D) 3√2 E) 2√5 X-2 -5 +

Oksijen Yayı 4. Uzunluğu cm türünden köklü sayılar ile ifade edilen cisimlerin boylarını ölçmek için özel bir cetvel üretiliyor ve bu cetvelin bir kısmı aşağıda veriliyor. A B C DEFG KLMN 0 √1 2√3+3√2 5 Örneğin, boyu 1 cm olan bir cisim, 0 ile C noktaları arasındaki uzunluk ile ölçülebilir. Bu cetvel, ardışık uzun çizgiler arası kısa çizgiler ile eşit aralıklara bölündüğüne göre, uzunluğu √2 √3 √4 cm olan bir cismin boyu 0 ile hangi nokta arasındaki uzunluk ile ölçülebilir? A) F B) G C) E D) K E) L

D ÖZEL ÖĞRETİM KURSU 11) Tam kare olmayan bir doğal sayının karekökünün; aralarında bulunduğu ardışık iki tam sayıdan hangi- sine daha yakın olduğunu bulmak için bu sayılardan hangisinin karesine daha yakın olduğuna bakılır. Örnek: 6 nın 2 ve 3'ten hangisine daha yakın olduğunun belirlenmesinde 2² ve 32 ile arasındaki farka bakılır. Hangisine daha yakınsa en yakın olduğu tam sayı odur. 4 br² 6 br² A) 4 √6-√4<√9-√6 olduğundan √6 nın en yakın ol- duğu tam sayı 2'dir. 9 br² Buna göre, tam kare olmayan kaç tam sayinin karekökünün en yakın olduğu tam sayı 5'tir? B) 5 __D)9 E) 10 C) 8

lar rak rpi- rtta or. so- muç H I Z V E R E NK 8. Bu tablonun her mavi karesine sayılar yazıldıktan son ra, her pembe kareye kendisiyle ortak kenara sahip olan tüm mavi karelerdeki sayıların çarpımı yazılmak- tadır. Örneğin; 1 √6 2√3 √3 N 2 Bazı kareleri pembe olan 3x3 lük tablo yanda verilmiştir. D) 2b√a 31+65 zb √2 √30 √ √ √a √a √b B) 2a/b √b 2√15 √5 Şekil 1 Şekil 2 Yukarıdaki Şekil 2 tablosunda pembe karelerdeki sayıların toplami a ve b türünden aşağıdakilerden hangisine eşit olur? A) 4ab ab √a √b C) 4a√a E) 4b√a √a