Olasılık Soruları

Lise Matematik
OlasılıkŞekildeki öndeki bank üç kişilik arkadaki bank dört kişi-
liktir. 3 erkek ve 4 kız üçü ön bankta dördü arka bankta
olacak ve erkekler yan yana olmak koşuluyla kaç farklı
er şekilde oturabilirler?
A) 120
C1-C
2-C
3-D
B) 266
4-A
5-B
C) 432
6-C
7-B
D) 556
8-E
9-C
E) 720
10-A
11-C
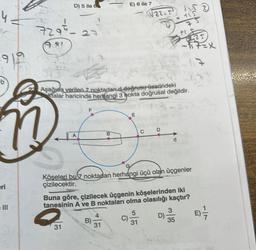
Lise Matematik
Olasılık6
eri
D) 5 ile
7ząń_.
72
31
F
5578
A
Aşağıda verilen 7 noktadan.d değrusu üzerindeki
talar haricinde herhangi 3 hokta doğrusal değildir.
3-217
B
B)
E) 6 ile 7
4
31
E
C)
22,5
C
Köşeleri bu 7 noktadan herhangi üçü olan üçgenler
çizilecektir.
5
31
D
Buna göre, çizilecek üçgenin köşelerinden iki
tanesinin A ve B noktaları olma olasılığı kaçtır?
d
1153
225
-117=x
112
3
35
D)-
e) /

Lise Matematik
Olasılıkra-
AVC
2
ve
2
Soru 12
6 sorunun sorulduğu bir sınavda 5 şıklı cevap anahtarı oluşturula-
caktır.
50
B) 65
2
3
4
5
6
50
ABCDE
Art arda gelen iki sorunun cevabı aynı olmayacağına göre, bu
sınavın cevap anahtarı kaç farklı şekilde oluşturulabilir?
A) 56
C) 360
D) 6.55
√/.4.4.4.4
E) 84
Du
pl
Lise Matematik
Olasılıkna
2.
ora
e
30.
eki gibi
Ideal KONDISYON
Örnek:
W
2
2
"
2
3
B
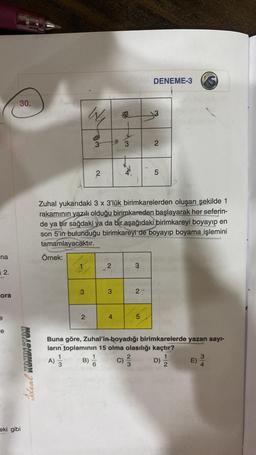
Zuhal yukarıdaki 3 x 3'lük birimkarelerden oluşan şekilde 1
rakamının yazılı olduğu birimkareden başlayarak her seferin-
de ya bir sağdaki ya da bir aşağıdaki birimkareyi boyayıp en
son 5'in bulunduğu birimkareyi de boyayıp boyama işlemini
tamamlayacaktır.
4
wok
3
3
2
C) 3/3
2
DENEME-3
5
2
5
Buna göre, Zuhal'in-boyadığı birimkarelerde yazan sayı-
ların toplamının 15 olma olasılığı kaçtır?
A) 1/3
B)
1
D) 2/2
E)
3

Lise Matematik
Olasılık23. Bir çekilişte toplam 10 bilet satılacak ve bu biletler-
den 4'üne birer hediye çıkacaktır. Her bilete hediye
çıkma olasılığı eşittir.
Buna göre, bir kişinin aldığı 3 bilete 2 hediye
çıkma olasılığı kaçtır?
A)
D)
5
18
B)
3
10
E)
7
20
C)
4
15
G
1
Y
2160
A
Y
I
N
EVI

Lise Matematik
Olasılık6
23. A = {1,3,5,6,7,9}
kümesinin elemanları kullanılarak yazılan
rakamları farklı 3 basamaklı tek sayılardan
rasgele alınan bir sayının 9 ile tam
bölünebilme olasılığı yüzde kaçtır?
A) 14
B) 15 C) 16
D) 17
1,3,51719
5.4. 5 = 100
7265
E) 18

Lise Matematik
Olasılık14. A =
A → 1₁2
A → 1₁3
A → 2,3
birdir.
A
(fof)(1)=2
(fof)(4) = 4
olduğuna göre,
1.
f(1) + f(3) = 5
11. f(2) + f(4) = 6
III. (fof)(3) = 3
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
D) I ve II
16
2,3,4} olmak üzere, f: A → A fonksiyonu bire
=5&
A → B
A12
E) Il ve Ill
E) ll
R (RU)) = 2
R (R(u)) = 4₁
(+)
C) Yalnızl
13

Lise Matematik
Olasılık8
27. İki hilesiz zar atılması deneyinde üst yüze gelen sayıların
toplamının a'dan büyük olma olasılığını hesaplamak iste-
yen Füsun aşağıdaki adımları uyguluyor.
AYT/ Matematik
1. Koordinat düzlemi çizerek x ve y eksenlerine 1'den
6'ya kadar olan sayıları yazıyor.
2. Daha sonra x- eksenindeki her bir noktayı y- eksenin-
deki her bir noktayla eşliyor.
3. Bu noktalarda toplamı a'dan büyük olanları işaretle-
yerek istenen durum / toplam durum yaparak cevaba
ulaşıyor.
Buna göre, Füsun iki zarın atılması deneyinde üst
yüze gelen sayıların toplamının 7'den büyük olma ola-
sılığını hesaplarken koordinat düzleminde kaç nokta
işaretlenmiş olur?
A) 8
B) 17
C) 23
D) 15
E) 24

Lise Matematik
Olasılık4. 9 kareden oluşan aşağıdaki oyun tahtasında üç oyuncu-
nun oynayacağı oyunun kuralları aşağıdaki gibidir.
●
●
Birinci oyuncu karelerden birine bir taş bırakır.
İkinci oyuncu, birinci oyuncunun bıraktığı kareyle or-
tak kenarı olmayan bir kareye bir taş bırakır.
• Üçüncü oyuncu da, diğer oyuncuların bıraktığı kare-
lerle ortak kenarı olmayan bir kareye taş bırakır.
Buna göre, bu üç taşın oyun tahtasındaki yerleşimi
kaç farklı şekilde olur?
A) 12
B) 18
C) 20
D 25
E) 28

Lise Matematik
OlasılıkC
35. Aşağıda bir oyun parkında boş durumda bulunan üç farklı
salıncak
gösterilmiştir.
AUUUA
Parka gelen Ozan salıncaklardan rastgele birine oturup
sallanıyor. Ardından Ozan gittikten sonra Seçil rastgele bir
salıncakta sallanıyor.
Buna göre, Ozan ve Seçil'den en az birinin ortadaki sa-
lincakta sallanmış olma olasılığı kaçtır?
A) = 1/3
B)
4
c)
5/9
D)
2

Lise Matematik
OlasılıkYayınları
36. İki farklı torbadan birinde 4 kırmızı, diğerinde ise 3 mavi
eis
1 sarı top vardır. İki torbadan biri rastgele seçilerek içinden
yine rengine bakılmadan rastgele bir top çekilecektir. An-
cak çekiliş yapılmadan az önce iki torbadan sadece birine
1 sarı top daha konuluyor.
Buna göre, çekilen topun sarı gelme olasılığı kaçtır?
D) 1/1
A)
9
40
B)
17
40
9
20
E)
7
40

Lise Matematik
Olasılık4. 9 kareden oluşan aşağıdaki oyun tahtasında üç oyuncu-
nun oynayacağı oyunun kuralları aşağıdaki gibidir.
•
•
Birinci oyuncu karelerden birine bir taş bırakır.
İkinci oyuncu, birinci oyuncunun bıraktığı kareyle or-
tak kenarı olmayan bir kareye bir taş bırakır.
Üçüncü oyuncu da, diğer oyuncuların bıraktığı kare-
lerle ortak kenarı olmayan bir kareye taş bırakır.
Buna göre, bu üç taşın oyun tahtasındaki yerleşimi
kaç farklı şekilde olur?
A) 12
B) 18
C) 20
D 25
E) 28

Lise Matematik
Olasılık3.
TYT/Temel Matematik
Ardışık iki ya da je pozitif tam sayının kareleri toplamına
eşit olan sayılara "kardışık sayılar" denir.
Ömeğin, 32+42-25 ve 12+22+32 = 14.olduğundan 25
ile 14 kardışık sayılardır.
Tamas 021
MJ GIS
Buna göre, aşağıdakilerden hangisi kardışık sayı de-
ğildir?
A) 110
62
16.
1 2 3
u
9
26
9
B) 113
22
C) 145 D) 184
U
16 (25
E) 194
us
64
36
68
Lu
TUS
25 (26 49
2
35
3
43. 64 81
5
16
??
5. Öz
bi
na
Co
m
us
64
81
ART

Lise Matematik
Olasılık5.
BÖLÜM 04 Test 18
1200 sayısının pozitif tam bölenlerinden biri seçiliyor
Buna göre, seçilen sayının 5 ile tam bölünebilme olasılığı
kaçtır?
C) 1/1/2
D) 1²/13
A)
6
Thoot 20
boo
3.00
St
B)
6
24. 1²:3
6. Aşağıda verilen altıgen üzerinde 6 kırmızı nokta ve iç
bölgesinde bir yeşil nokta verilmiştir.
39116
03.1
1420
ve rune sh

Lise Matematik
OlasılıkÖrnek 9
Esmer ve sarışınların oluşturduğu 14 kişilik bir
grup ile ilgili aşağıdaki bilgiler bilinmektedir.
• Bu gruptan rastgele seçilen 6 kişiden en az biri
kesinlikle erkektir.
• Bu gruptan rastgele seçilen bir kişinin esmer ve
sarışın olma olasılıkları birbirine eşittir.
Bu gruptan rastgele seçilen bir kişinin sarışın
2 dir.
erkek olma olasılığı di
Buna göre, bu gruptan rastgele seçilen bir kişinin
esmer bayan olma olasılığı kaçtır?
kadın

Lise Matematik
Olasılık30. Dört soruluk bir sınava giren Sinem'in girdiği bu sınav-
da her sorunun puanı ve Sinem'in bu soruları doğru
yapma olasılığı aşağıdaki tabloda verilmiştir.
Soru No
1
2
3
4
Puan
40
25
20
15
Sinem'in Doğru Cevap
Verme Olasılığı
%25
A) %17 B) %15 C) %13
%40
%75
%60
Buna göre, tüm soruları cevaplayan Sinem'in bu
sınavda en az 80 alma olasılığı nedir?
D) %9
E) %7
15
