Polinom Kavramı ve Polinomlarla İşlemler Soruları

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler7. Başkatsayısı 2 olan üçüncü dereceden bir P(x)
polinomu (x + 1) ile tam bölünebiliyor.
P(x) polinomunun bir çarpanı (x - 1) ve sabit
terimi 12 olduğuna göre, P(x) polinomunun
(x + 2) ile bölümünden kalan kaçtır?
A) -18
B) -20
C) -24
D) -36 E) 48
![B
2x3 + 5x2 + 4x + 4
4.
A
6.
+
Feray, yukarıdaki (2x3 + 5x2 + 4x + 4) br uzunluğundaki
[AB]'na n tane pergelin her birini (x?
1) br açarak
yanyana şekildeki gibi yerleştirdiğinde en sonda 5 br yer
artıyor.
n.
2.
3.
AM
A
LO
Buna göre, n kaçtır?
A) 11
B) 13
C) 15
D) 12
E) 10](https://media.kunduz.com/media/question/raw/20211111184540416421-1812954.jpeg?w=256)
Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerB
2x3 + 5x2 + 4x + 4
4.
A
6.
+
Feray, yukarıdaki (2x3 + 5x2 + 4x + 4) br uzunluğundaki
[AB]'na n tane pergelin her birini (x?
1) br açarak
yanyana şekildeki gibi yerleştirdiğinde en sonda 5 br yer
artıyor.
n.
2.
3.
AM
A
LO
Buna göre, n kaçtır?
A) 11
B) 13
C) 15
D) 12
E) 10

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler5.
(6+P(x))" polinomunun sabit olmayan P(x) polinomu
ile bölümünden kalan, P(x - 1)+Q(x) polinomunun
(x-3) ile bölümünden kalana eşittir.
P(x+1) 'in katsayılar toplamı, Q(3 - x)'in sabit
teriminin 2 katı olduğuna göre, P(x+2)'nin sabit
terimi kaçtır?
A) 4
B)-2
C) -4
D) 24
E) 12
UG

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler30. Başkatsayısı 1 olan ikinci dereceden gerpal katsay be
P(x) polinomunun sifirlan ardışık doğal sayılardır
:
P(x) polinomunun sabit terimi 12 olduğuna göre,
P(x) polinomunun x-2 ile bölümünden kalan kachr?
B) 3
A) 2
C) 4 D5

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler100. (x-2)
7. Baş katsayıları 1 olan P(x), Q(x) ve R(x) polinomları
sırasıyla üçüncü, ikinci ve birinci derece birer polinom
olmak üzere aşağıdaki kâğıdın üzerine v
P(x) < 0 ve Q(x). R(x) < 0
eşitsizliklerinin tabloları çizilmiştir.
Lee
2
P(x)
-
+
(*
ST
2
4
+
+
RELLIER
Q(x)•R(x)
Buna göre, P(x) polinomu;
ma
II. R(x)
III. R? (x)
polinomlarından hangilerine kesinlikle tam bölünür?
A) Yalnız!
B) Yalnız H
C) I ve 11
DI ve III
E) I, II ve III
DOM
P(x)=1.22-2² (x-4)
QG). RL) . (x-2) (2-4

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerA) X
9-3 +1
16. Aşağıdaki bulmacada mavi renkli kutucuklardaki polinomların
katsayıları sıfırdan farklı bütün terimleri ok uçlarının gösterdiği
satırdaki veya sütundaki kutucuklara, en büyük dereceli
terimlerinden başlanarak ve her kutuda farkli dereceli bir
terim olacak şekilde yazılmaktadır. Örneğin; bulmacada
P(x) = 2x3 + 8x² - 4x şeklindedir.
WAS
SO
POLINOM BULMACA
Q(x) R(x)
P(x)2x38x2-4x
K(x)
OT
TI
()
al
Bulmacada P(x) polinomunun katsayıları toplamı, R(x)
polinomunun sabit terimine eşit ve R(x) polinomunun K(x)
polinomuna bölümünden kalan 14 olmaktadır.
Buna göre, Q(x) polinomunun K(x) polinomuna
bölümünden kalan kaçtır?
- SA
A) 24
B) 27
C) 31
D) 38
E) 44
13.D 14.B 15.C 16.C
UcDört
Bes
11

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerAşağıda verilen CAB dik üçgeninde,
C
H
B
DH = X2 .1 birim
HB| = x2 + x + 1 birim
DHB üçgeni (DH) boyunca katandiĝında B noktası A nok-
tasıyla çakışmaktadır.
C
Katlama sonrasında oluşan
AHDC dörtgeninin alanını ifa-
de eden polinom P(x) polino-
mudur.
A
H
Buna göre, P(x) polinomunun sabit terimi kaçtır?
5
A)
B) 2
Non
D) 1
c)
Lise Matematik
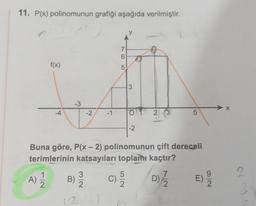
Polinom Kavramı ve Polinomlarla İşlemler11. P(x) polinomunun grafiği aşağıda verilmiştir.
y
7
6
f(x)
5
3
-3
5
X
-4
-2
-1
2 3 3
-2
Buna göre, P(x - 2) polinomunun çift dereceli
terimlerinin katsayıları toplam kaçtır?
)
A)
1
2
B)
3
)
2.
5
C)
2.
2
D)
D)
2
9
E)
Ol
3
1 2

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlera
TIP 30
- 6999 - com
=
-
P(x), 3. dereceden bir polinom olmak üzere,
P(1) = P(2) = P(3) = O'dır.
P(x + 2) polinomunun x - 2 bölümünden kalan 12 olduğuna
göre, P(x - 2) polinomunun katsayılar toplamı kaçtır?
A) -48
B) -24 C) 12 D) 24 E) 48

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler11.) Pozitif a tam sayısının karesinin 11 eksiği x sayısına
eşittir.
x=92_11
P(a) = x² – 3x - 10
-
2
polinomu tanımlanıyor.
i-
Buna göre,
A= -3
I. P(a) polinomu a + 3 ile tam bölünür
5
tonguç kampüs
II. Pla + 3) polinomunun sıfırlarının toplamı -12 dir.
-
III. P(Pla + 1)) polinomunun a - 3 ile bölümünden
kalan 144 tür.
ifadelerinden hangileri doğrudur?
C) Yalnız III
A) Yalnız
B) Yalnız 11
D) II ve III
E) I, II ve IN

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler+
*
P(x) = (2x - 3)2. (x + 2) polinomuna eşit Q(x)
polinomunun terimleri, x'in azalan kuvvetlerine göre,
sıralandığında katsayılar sırasıyla a, b, c, d, e, f'dir.
a+c+e
Buna göre,
oranı kaçtır?
b+d+f
3
1
3
A)
)
C)
D) ZEE
2 4
B)
20
10
17
26
13

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler8.
Üçüncü dereceden bir P(x) polinomu için, P(x + 3)
polinomunun katsayılar toplamı 23 tür.
P(1) = 2 plul_23
P(2) = 3
P(3) = 4
olduğuna göre, P(x) polinomunun sabit terimi
kaçtır?
A) -21
B) -19 °C) -17 D) -15
E) -13

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerÖnce Konuyu
Tanımak
Lazam
Klasikle
Sorul
12
9. P(x) polinomunun baş katsayısı negatif gerçel sayı olmak
üzere
(+6)
P(2. P(x) - 3) = 9+ 8x
Palk axtb.
olduğuna göre,
P(x) + P(x - 2)
aşağıdakilerden hangisidir?
A) -4x + 6
B)-2x - 1
C)-2x + 4
E) -4x - 1
D) -4x + 2
1.

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerÖSYM TADINDA 1
Başkatsayısı 3 olan 2. dereceden bir P(x) polinomu için
P(1) - P(-1) = -2
olduğuna göre,
3x²
3 - 3 plo)= -2 2
P(x) = 0
(C-
eşitliğini sağlayan x değerleri toplamı kaçtır?
=
1
3
A) ;
B) 1
C)-1
-
D)
Ź E)
2
3
E)
2
3
X
0. Q(x), sabit bir polinom; P(x), ikinci dereceden bir polinom
olmak üzere
(0) 12x2 – 24x x² Q(x)=

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerEn yake
dereceden reel katsayli bir PO DO
farkh koku Po ve Pat degerleridir.
bo-
Buna göre P(-2) degeri nedir?
D) E
16
N},
P(x)= ax + bxts
P(x) = 2x² 6x+C
9.
Reel katsayılı ve baş katsayısı -2 olan 4. derece-
den bir Pbx) polinomu her x reel sayısı için
P(x) - P(-x)=0
AY MATEMATIK SORU BANKASI
şartini sağlamaktadır
P(1)=P(3)=0 ise P(-2) ifadesi kaçtır?
A) 30 B) 28C) 24 D) 18 E) 12
P(x) = -2x + 68tcxt date
Pfa)
).

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler27.
P(x) polinomunun x-3 ile bölümünden kalan 4 ve bölüm
Q(x)'dir. Q(x) polinomunun x + 3 ile bölümünden kalan
4'tür.
Buna göre, P(x) polinomunun x? - 9 ile bölümünden
kalan aşağıdakilerden hangisine eşittir?
A) 4x + 8
B) 4x + 3
C) -4x+ 2
D) - 4x + 4
EY_4X
- 4x + 16
PS2)
