Polinom Kavramı ve Polinomlarla İşlemler Soruları

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler3
14 Polinomlarda bölme işleminden kalanın bulunması ile ilgili bir
kısayol anlatmak isteyen Yasin Öğretmen, tahtaya aşağıdaki
örneği yazıp aşağıdaki açıklamayı yapmıştır.
7315
13
13 5
ZA
"73 sayısının 15 ile bölümünden kalan 13 tür. 73 sayisinin 3 ile
bölümünden kalan için 13'ün 3 ile bölümünden kalanına ba-
kabiliriz. Her ikisinde de kalan t'dir. Aynı durum 5 to bolümün
den kalanı bulunurken de gegarlidir."
Bu örneğin polinomiar cineçerli olunu beter Yasin
Öğretmen aşağıdaki soruyurmuştur
"P(x) polinomunun 27 Dominden kalan 3
olduğuna göre, P(x) polinomunune - 3x + 9) ile bolomünden
kalan kaçtır?"
Buna göre öğrencilerin soruya vermeleri gereken doğru
cevap aşağıdakilerden hangisidir?
A) 3x - 1
B) 3X9
C) 3x 15
0) 5x - 15
Fr5x + 15
x²3
28-X +3

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerBaşkatsayısı 1 olan ikinci dereceden bir P(x) polinomu
için
P(-1) • P(1) = 0
P(-1). P(2) = 0
P(O) = 4
= 4
olduğuna göre, P(x) = 0 eşitliğini sağlayan x değerleri
toplamı kaçtır?
D) 5
E)3
C) 6
A) 4
B) 2

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler10. Gerçel katsayılı ve dördüncü dereceden olan bir P(x)
polinomu her x gerçel sayısı için,
P(x) < 0
eşitsizliğini sağlıyor.
P(-1) = 0
P(0) = -12
P(2) = 0
olduğuna göre, P(3) kaçtır?
A) -48
B) -36
C) -24
D) -12
E)-6

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerEge Yayıncılık
3.
7.
P(x) = (x2 - 2x + 1)2 - 3x2 + 4
polinomunun x2 + x + 1 ile bölümünden kalan
nedir?
P(x) = x3 - 2x2 + ax + b
polinomu (x - 2)2 ile tam bölünebildiğine göre, a+b
kaçtır?
A) 6x + 2
B) 6x-2
C) -6x + 2
A) 2
B) 3
C) 4
D) 5
E) 6
D) -6x-2
E) -3x + 2

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerlio
P(x) bir polinom olmak üzere,
P(x+2) - X+5
x² - 1
ifadesi de bir polinomdur.
Buna göre, P(x) polinomunun x2 - 4x + 3 ile bölümün-
den kalan aşağıdakilerden hangisine eşittir?
A) 3x - 1
B) X-1
C) -x + 11
D) X-7
E) -x + 17

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerP(x + 2) polinomunun x 5x + 1 ile bolumunden ka
lan 6x + 1 dir.
1
Buna göre, P(x - 1) polinomunun x? - 11x + 25 ile
bölümünden kalan aşağıdakilerden hangisidir?
2
.
A) 6x - 17
B) 6x + 5
C) 5x 8 8
D) 5x + 8
E) 4x + 11
a

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerI SORULAR
MLAR
BÖLME
5.
P(x) = x + 1 ve Q(x) = x - 1 polinomları veriliyor.
P4(x) + (ax + 1). Q(x)
polinomunun Q?(x) ile bölümünden kalan P(x) + 14
olduğuna göre, P(a) değeri kaçtır?
A) -31
B) -30
C) -29
D) -32
E)-27
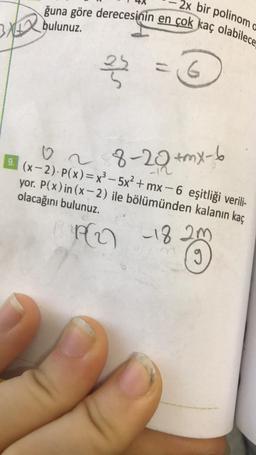
Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerğuna göre derecesinin en çok kaç olabilece
2x bir polinom
bulunuz.
es
o
9. (x - 2). P(x)= x3 – 5x² +mx - 6 eşitliği verili-
yor. P(x) in (x - 2) ile bölümünden kalanın kaç
olacağını bulunuz.
0 28-29 tmx-6
-
(
P20 -18
-182m
9

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler11. P(x) ve R(x) birer polinom olmak üzere R(x) | P(x) gösterimi,
R(x) polinomunun P(x) polinomunu tam böldüğünü ifade eder.
(x - 2)| P(x)
(x-3)| P(x)
(x + 2)| P(x)
P(x + 3) polinomunun x® polinomu ile bölümünden elde
edilen bölüm 2'dir.
.
Ploo.
& YAYINLARI
Buna göre, P(x + 1) üçüncü dereceden polinomunun sabit
terimi kaçtır?
3
E) 12
D) 15
C) 18
A) 24
B) 20
![14.
SO
Q(+5)
polinomunun derecesi 3
P(x3)
Q®(x) • P(x2 + 1) polinomunun derecesi 17
olduğuna göre, (P(2x - 1)] polinomunun derecesi
kaçtır?
6 lei nebümblod oll + x nunumonllog
A) 12 B) 18 C) 9
D) 24 E) 6
od let
( Sx+(3-X)
-](https://media.kunduz.com/media/question/seo/raw/20220402181227965676-2003865_FjwqfGnJQ.jpeg?w=256)
Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler14.
SO
Q(+5)
polinomunun derecesi 3
P(x3)
Q®(x) • P(x2 + 1) polinomunun derecesi 17
olduğuna göre, (P(2x - 1)] polinomunun derecesi
kaçtır?
6 lei nebümblod oll + x nunumonllog
A) 12 B) 18 C) 9
D) 24 E) 6
od let
( Sx+(3-X)
-

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerA) 18
B) 17
OTTA DITS elin
14
E) 40
bol=u
n-2=6
=
Tn=8
To=5
(3x2 - x + 2).(-4x3 + x - 1)
10
6
P(x)
c
polinomunun x3 lü teriminin katsayısı kaçtır?
D) 3
E) 5
e-5
alabile-
A)
-8
B)-7
34
12x+3x² – 3x2 + 4x
us
E) 15
-
7.
(5x3 - ax2 + 4x - 2). (4x2 + 3x + a)
çarpımında x lü terimin katsayısı 30 olduğuna
2,5,10

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler.
C
P(x) = x4 - x3 + ax2 + bx + c polinomu veriliyor. a. c = 3.b
ve P(x + 1) polinomu x ile tam bölünebildiğine göre,
(a+b)(c+b)
ifadesinin değeri kaçtır?
atc
Hot-1tet 6-1+ c
A) 2
B) 3
C) -1
D) -2
E)-3

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlertöder
2A DENEME SINAVI
720
360
5.
80
P(x), altıncı dereceden bir polinomdur.
P(3) = P(4) = P(5) = P(6) = P(7) = P(8) = 6! ve
P(2) = 0 olduğuna göre, P(9) kaçtır?
A) -24 B) O
C) 1
D) 120
bo
E) 720
6.5.4. 2. 2
P(x) = a (x-3) (x-4) (x - 5)(x-6) 1.
- 1-2. - 4 - 5 - 6
-3-4-5-6
6
tn 20a +720
9--1
120
Gerçel katsayılı ve başkatsayısı 6 olan dördüncü derece-
den P(x) polinomu için,
P(-x) = P(x) eşitliği sağlanıyor.
31-2) = 4,

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler6
4
3
+
P(x) = (m – 3)x® + mx* + (m – 1)x® + 3x + m + 1
polinomunun derecesi 4 olduğuna göre, bu poli-
nomla ilgili,
1. Başkatsayısı 3'tür.
II. Sabit terimi 4'tür.o
.
III. Katsayıları toplamı 12'dir.
ifadelerinden hangileri doğrudur?
A) Yalnız 11
B) I ve II
D) Il ve III
C) I ve III
E) I, II ve III

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler5
-
3. Gerçel sayılar kümesinde tanımlı
P(x) = 4x + 5x - 6
polinom fonksiyonu için
. Bire birdir.
II. Bir tane gerçel kökü vardır.
W. Her XER için P(-x) = -P(x)'tir.
.
ifadelerinden hangileri doğrudur?
P'(x) = 20x4+5
s(4x4+1)-2
Matematik
A) Yalnız
B) Yatz IT
C) Yalnız III
E) I ve IIT
D) I ve II

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerVOF
33
Bilye üreten bir fabrikada bilyeleri depolamak için iki
tür koli kullanılmaktadır.
Bu kolilerden küçük olanına x + 4, büyük olanına ise
x² + x tane bilye konulabilmektedir.
Bu kolilerden x tane küçük ve x + 1 tane de büyük koli
kullanılarak, üretilen tüm bilyeler depolanmıştır.
Depodaki tüm bilye sayısı P(x) polinomu ile gösteril-
mek üzere, bilyelerin hepsi, her biri x - 1 tane bilye
alan kolilere doldurulmuştur.
Buna göre, kullanılacak koli sayısı ve koli dışında
kalan bilye sayısı aşağıdakilerden hangisinde doğ-
ru olarak verilmiştir?
kwurk
Koli Sayısı
Artan Bilye
Sayısı
A)
x² + 4x
P(1)
B)
x² +9
P(1)
C) 2x² + 2x
P(-1
D x² - 4%-9
P(0)
E) 1x² + 4x + 9
4x + 9
P(1)
b
xty
+
1xt x(x
