Polinom Kavramı ve Polinomlarla İşlemler Soruları

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerTest - 4
Test
1.
10. Dokuz terimli bir Plx - 2) polinomunun katsayılarından üç
tanesi 3 ve kalan altı tanesi -6 dir.
e
dur.
Buna göre, P(x) polinomunun (x + 1) ile bölümünden
kalan kaçtır?
A) -12 B) -15 C) -18 D) -24
E) -27
E) 4

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerX
2
- 10. P(x) polinomunun x2 - 16 ile bölümünden kalan
(3x + 1), x? - 25 ile bölümünden kalan (2x - 7)
olduğuna göre, P(x) polinomunun x? + x - 20 ile
bölümünden kalan aşağıdakilerden hangisidir?4/-
s
2
-
A) 3x + 10
X – 10
B)
3
x + 10
C)
3
D)
10x + 1
3
E)
10x – 1 (x+4)(x)
3
5,- S
P(4)=13
pe
Pah) =-11
P (5)=3
PES)= -97
P(x) = Q = 4) (x+S). R(A)
4
ayıncılık

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler9.
P(x) = (3x2 – 3x + 2) 3
polinomunun tek dereceli terimlerinin katsayıları toplami a,
çift dereceli terimlerinin katsayıları toplamı b dir.
Buna göre, a + b toplamı kaçtır?
A) 2
B) 4
C) 8
D) 16
E) 24

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler=
TE
15, Pbx) polinom olmak üzere, P(m) = n ve P(I) = q ise
m-r sayısı n-q sayısını tam böler.
P(7) = r + 5
-
P() = 4r - 21
olduğuna göre, r'nin alabileceği kaç farklı tam sayı
değeri vardır?
A) 1
B) 2
C)3
D) 4
E) 5

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler2. P(x) polinomunun x ile bölümünden kalan 2, x + 2 ile
bölümünden kalan 4 olduğuna göre; x2 + 2x ile bölü-
münden kalan kaçtır?
Ax + 2
B)-X-2
C) 2x - 1
D) 2x + 1
E-X + 2
2v+2)
+2
CAYINLARI
Pro)=2
(
L2) -

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler9. p bir gerçek sayı olmak üzere,
A= p - 2
B=p + 2
eşitlikleri veriliyor.
Buna göre,
p3 – 2p2 – 4p + 8
ifadesinin A ve B türünden eşiti aşağıdakilerden han-
gisidir?
A) A. B3
B) AS.B
C) A2.B
D A.B2
E) A3 + B3

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler-
Üçüncü dereceden bir P(x) polinomunun (x - 2)
ile bölümünden kalan (x + 1) dir.
P(x) polinomunun sabit terimi 7 olduğuna göre,
P(x) polinomunun (x + 1) ile bölümünden kalan
aşağıdakilerden hangisidir?
+
A) 1 B) 3
C) 5
D) 7 E) 9

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler2.
P(x) ikinci dereceden bir polinomdur.
P(x) polinomunun x² + x ile bölümünden kalan (2x - 1)
ve P(x) polinomunun katsayılar toplamı -3 olduğu-
na göre, P(x) polinomunun x- 2 ile bölümünden ka-
lan kaçtır?
5.
A)-6
B) -8
C) -9
D) -10
E)-12

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerx= 3
3. P(x) ve Q(x) polinomlarının x-3 ile bölümle-
rinden kalanlar sırasıyla 6 ve 2 dir.
P(x) + m. Q(x) polinomu x - 3 Ne tam bölüne-
bildiğine göre, m kaçtır?
X-
30
x=3
P(x) + m. a (x)
P(3)=6,
2 (3)=2

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerX +5
5
925:0)
24-
P(x) polinomunun x2 - 4 ve 2.9 ile bölümlerinden
kalanlar sırasıyla 2x + 3 ve x + 7 dir. Buna göre,
P(x) in x2 - 5x + 6 ile bölümünden kalan nedir?
P(x) polinomunur
kalanlar sırasıyla
P(x) in x - 4 le
A) x + 5
B) 2x + 4
D) 4x - 2
C) 3x + 1
E) 4x - 1 1
A) x + 9
D) 2
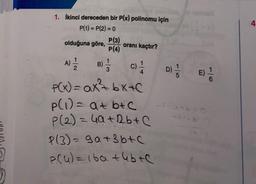
Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler1. İkinci dereceden bir P(x) polinomu için
P(1) = P(2) = 0
4
olduğuna göre, oranı kaçtır?
P(4)
P(3)
A)
2
B)
3
D)
E)
)
=
-latboo
P(x) = ax² bx+c
p(1) = at btc
P (2) = 40+2b + c
P(3) = ga+b+c
P(u) = iba tebte
-
![P(x) bir polinom olmak üzere
[x3 + P(x)]2
polinomunun (x3 - P(x)) ile bölümünden kalan
3 x2 olduğuna göre, P(x) polinomu aşağıdakilerden
hangisi olabilir?
redxb
X
A) Ž B) 2x Cx D) 4x E)
2
X
4
7.A 8.E 9.A](https://media.kunduz.com/media/question/seo/raw/20220306162846123193-4034300_t8radLXnF.jpg?w=256)
Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemlerP(x) bir polinom olmak üzere
[x3 + P(x)]2
polinomunun (x3 - P(x)) ile bölümünden kalan
3 x2 olduğuna göre, P(x) polinomu aşağıdakilerden
hangisi olabilir?
redxb
X
A) Ž B) 2x Cx D) 4x E)
2
X
4
7.A 8.E 9.A

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler11. Bir P(x) polinomunun x2 - 4 ile bölümünden bölüm Q(x),
kalan x + 3'tür.
Buna göre, P(x)'in x - 2 ile bölümünden bölüm
aşağıdakilerden hangisidir?
A) (x + 2). Q(x) + 1
C)(x + 2). Q(x) - 1
E)(x + 2). Q(x)
B) (x - 1). Q(x) – 1
D) (x - 1). Q(x) + 1
A

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler4. Katsayıları tam sayı olan dördüncü dereceden bir P(x)
polinomunun başkatsayısı 2 olup 3 farklı gerçel kökü
vardır.
P(1) = P(2) = 0
P(-2)= 72
olduğuna göre, P(4) değeri kaçtır?
A) 100
B) 112
C) 120
D) 180
E) 200

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler-
8. Birinci dereceden bir P(x) polinomunun (x-2) ile bölümün-
den kalan, (X-P(1)) ile bölümünden kalana eşittir.
Buna göre, P(x) polinomunun (x - 1) ile bölümünden
kalan kaçtır?
lomunun (* = "
A) 3
B) 2
C) 1
D) -2
E) -3

Lise Matematik
Polinom Kavramı ve Polinomlarla İşlemler17. 3. dereceden bir P(x) polinomu ile ilgili
aşağıdaki bilgiler verilmektedir.
11.
P(x) polinomu x2 +1 ile tam bölünen
a a
bir polinomdur.
• P(x) polinomunun baş katsayısı -2
dir.
P(x) polinomunun sabit terimi - 12 dir.
Bu bilgiler yardımıyla
a) P(x) polinomunun katsayılar toplamını
bulunuz.
b) P(x+3) polinomunun x+5 ile bölü-
münden kalanı bulunuz.
12.
