Polinomlarla İşlemler Soruları

30. P(x) polinomu, ya ge- daha arklı P(x) = ax + 2 Olax+2)+2=4x+b olarak tanımlanıyor. ax+ 20 +2-6x +b P(P(x)) = = 4x + b CHX+2 olduğuna göre, P(b)'nin alabileceği değerler topla- mi kaçtır? abt2 A) 24 B) 20 C) 18 D) 15 E) 12 30 49 231 49 Günde TYT Matematik

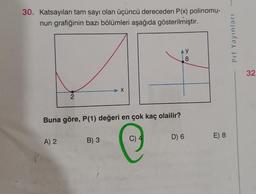
30. Katsayıları tam sayı olan üçüncü dereceden P(x) polinomu- nun grafiğinin bazı bölümleri aşağıda gösterilmiştir. Prf Yayinlan y 8 32. 2 Buna göre, P(1) değeri en çok kaç olailir? D) 6 A) 2 C) E) 8 B) 3

9-9+1=11 16. Aşağıdaki bulmacada mavi renkli kutucuklardaki polinomların katsayıları sıfırdan farklı bütün terimleri ok uçlarının gösterdiği satırdaki veya sütundaki kutucuklara, en büyük dereceli terimlerinden başlanarak ve her kutuda farkli dereceli bir terim olacak şekilde yazılmaktadır. Örneğin, bulmacada P(x) = 2x + 8x² - 4x şeklindedir. POLİNOM BULMACA Q(x) R(x) P(x) 2x3 8x2 -4x K(x) 5 Bulmacada P(x) polinomunun katsayıları toplamı, R(x) polinomunun sabit terimine eşit ve R(x) polinomunun K(x) polinomuna bölümünden kalan 14 olmaktadır. Buna göre, Q(x) polinomunun Kx) polinomuna bölümünden kalan kaçtır? A) 24 B) 27 C) 31 D) 38 E) 44 13.D 14.B 15.C 16.0

13. Matematik Öğretmeni Zeynep Hanım öğrencilerin- den Hatice'yi tahtaya kaldırıyor ve "Hatice, şimdi sana bazı koşullar söyleyeceğim ve senden bu ko- şullara uygun bir polinom yazmanı isteyeceğim." di- yor. Zeynep Hanım'ın söylediği koşullar şu şekildedir: Bir bilinmeyenli, üçüncü dereceden ve katsayıları birbirinden farklı pozitif tam sayılardan oluşsun. Başkatsayısı 4 ten küçük olsun. Katsayılar toplamı 11 olsun. Buna göre, Hatice, bu koşullara uygun kaç farklı polinom yazabilir? At A) 6 B) 12 C) 18 D) 24 E) 30 P(x) = x² +6x² + cxtd. <4 P(a)= abac+d=11 btct d= 8 3. 1 25 2 b+c+d=9 7 3:15 htt 612 4.5.2 7 the di 35 5 3 23 642 35 D Stee 513 ni SSUPARA 12 5 14. Aşağıda sağ ve sol kısımlarında dörder adet kart yerleştirme bölmesi olan bir cüzdan gösterilmiştir. 90 5 1 2

Baş kat sayısı 2 ve kat sayılar toplamı 10 olan 3. derece- den bir P(x) polinomu, (x2 + 1) ile tam bölünüyor. Buna göre, P(x) polinomunun tek dereceli terimlerinin kat sayıları toplamı kaçtır? :) 0 B) 1 C) 2 D) 3 E) 4

9. 11. Başkatsayısı 2 olan ikinci dereceden polinom olan P(x) için P(1) = P(-2) = 0 olduğuna göre, P(x + 1) - P(x) ifadesi aşağıdakilerden hangisine eşittir? B) 8x - 2 C) 6x-2 A) 4x + 4 D) 6x + 4 E) 8x + 4

- 2X 3. P(x) = x + x? x2(x+1) 6. Q(x) = x + 1 olduğuna göre, P(x) ve Q(x) polinomlarının en büyük ortak bölen ve en küçük ortak kat polinomlarının çarpi- minin derecesi kaçtır? ka A B) 2 A) 1 C) 3 D) 4 E) 5 X

5. P(x) x²-x-2 ifadesi bir polinom belirttiğine göre, P(x + 4) polinomu 1. x + 5 II. x + 1 III. x + 2 polinomlarından hangilerine kesinlikle tam bölünür? A) Yalnız! C) I ve III B) Yalnız 10 D) II ve III E) I, II ve III 4.D 5.

6. P(x), başkatsayısı 1 olan üçüncü dereceden bir polinom- dur. Bu polinomla ilgili olarak • P(x) polinomu x + 8 ve xe tam bölünmektedir. P(x) in birinci türevi x + 2 ye tam bölünmektedir. bilgileri verilmektedir. Buna göre, P(-4) kaçtır? LA -16 B) -12 C) -8 D) -4 E) 2

12.) Uğur Öğretmen tahtaya aşağıdaki gibi bir kare dik priz- ma ile bir dikdörtgen çizip prizmanın ayrit uzunlukları- i ve dikdörtgenin kenar uzunluklarını birim cinsinden üzerlerine yazıyor. X X + 2 x + 3 X Ardından öğrencilerinden kare dik prizmanın hacmini belirten ifadeyle P(x) polinomu, dikdörtgenin çevresini belirten ifadeyle Q(x) polinomu oluşturmalarını istiyor. Son olarak Uğur Öğretmen öğrencilerinden P(x) polino- munun Q(x) polinomuna bölümünden kalanı bulmalarını istiyor. Buna göre, öğrencilerin bulmaları gereken sonuç aşağıdakilerden hangisidir? A)-4 B)-2 C) 1 D) 2 E) 5

8. P(2x)'in 2x – 3 ile bölümünden kalan 8 P(x + 1)'in (x - 1)2 ile bölümünden bölüm Q(x – 3), kalan 2x Q(x + 1)'in (x + 2)2 ile bölümünden kalan 2x + a olduğuna göre, a kaçtır? A) 11 B) 8 C) 5 D) 4 E) 2 5.B 6.E 7.A 8.B

MATEMATİK TESTİ 1. Bu testte 40 soru vardır. 18x –9x 2. Cevaplarınızı, cevap kâğıdının Matematik için ayrılan kısmına işaretleyiniz. 3. R=-1, 2i 2i 1. a ve b gerçel sayılar ve P(x) bir polinom olmak üzere, P(x) = (2a - 3)x3 - 4x² + (6 – 3)x + 2 polinomu (x² - x - 2) ile tam bölünebiliyor. Buna göre, a.b çarpımı kaçtır? XZ 2+X xxth A)-6 B)-3 C)-1 D) 2 E)4 eşitliğ Buna A) O Plx)=(29–3) x?x — 412+x) +622)x+2 2 +)ex - 8-Ux+ bx-3x+2

P(x) = x5 - 79x4 - 80x3 + x2 - 79x + 78 polinomu x - 80 ile bölündüğünde kalan kaçtır? A) 162B ) 158 C) 80 D) 79 E) 78

Burad yerin 3 . 1. P(x) polinomu için (3x – 1). P(x - 1)+ P(x - 2) = 3x² + 12x – 1 eşitliği veriliyor. P(x) polinomunun sabit terimi 5 ise, katsayıla- rinin toplamı kaçtır? A) E) 2 6 C)4 B) 5 D) 3

karekök 17. P(x) polinomu için P(2x) + P(x - 1) + P(x + 1) = 12x - 3 olduğuna göre, P(x) polinomunun katsayıları- nin toplamı kaçtır? Proso A)-2 B)-1 C) 0 D) 1 E) 2 POO + P(-1) AP(1) = -3 Plot

karekök 22 4. P(x) polinomunun (x + 1)(x2 - 4) ile bölümünden kalan x + 5x + 2'dir. Buna göre, P(x) polinomunun x² + 3x + 2 ile bölümünden kalan kaçtır? 0 A) 3x - 1 B) 2x + 1 C) 3x D) 2x Ex