Üslü İfadeler ve Denklemler Soruları

Lise Matematik
Üslü İfadeler ve DenklemlerBir inşaat firması yaptığı 4 farklı blokun banyolarının tabanina aşağıda verilen fayanslardan belirtilen saylarda
kullanacaktır.
A Blok (121 adet)
C Blok (225 adet)
B Blok (160 adet)
D
D Blok (289 adet)
Banyoların tabanlarının kenarlarında kullanılan fayans sayısı 1'den fazla olduğuna göre aşağıda veri-
len fayanslardan hangilerinin döşendiği banyoların tabanı kesinlikle kare şeklindedir?
Al
8)

Lise Matematik
Üslü İfadeler ve Denklemler2.
3
1/44
54
2.3 208
22 -
3
103
entr
Bilgi: a, m, n birer tam sayı olmak üzere (a # 0) ama" = am+ndir. Dairenin alanı лr² dir. (r: yarıçap)
halinin görseli verilmiştir. Karesel şekle sahip perde yarım daire şeklindeki perdeyi tamamen kapatabilecek en k
Şekil-l'de, Özkan'ın odasına ait yarım daire şeklindeki penceresi, Şekil-II de ise Şekil I deki pencerenin perdesini
sahiptir.
la
-54
132
3
r
Z
2
6
84
√2
Şekil - I
(Perde açık hali)
25
A
165
Yarım daire şeklindeki pencerenin ahşap ve cam kısmının toplam alanının 8
deki karesel perdenin görünen yüzeyinin alanı kaç cm² dir? (n = 3)
A) 34
ghe
37
B) 36
C) 38
-72
3
B22
32797, 124
r=/31
2
Şekil - II
(Perde kapalı hali)
"mla
6
J
28 4
D) 310
3
Sare
T
17. Baz
ma
diz
cm² olduğu bilindiğine göre Se
91₁125
√34
3
nobilmeleri için dizmis olduğu taslar görs

Lise Matematik
Üslü İfadeler ve Denklemlerebob
2. Boyutları 65 cm, 78 cm ve 104 cm olan dikdörtgenler
prizması şeklindeki bir depoya, kenar uzunluğu en
büyük olan küplerden yerleştirilecektir.
Küpler eş olacak şekilde kaç küp yerleştirilir?
A) 240 B) 200 C) 180 D) 120 E) 80

Lise Matematik
Üslü İfadeler ve Denklemler8.
"BİLGİSAYAR"
kelimesinin harflerinin yerleri değiştirilerek, sesli
harfle başlayıp sesli harfle biten anlamlı ya da anlam-
sız kaç farklı kelime yazılabilir?
A) 6!
B) 3-7!
C) 8!
D) 3-8!
DIA
E) 9!
ullmatematik
11
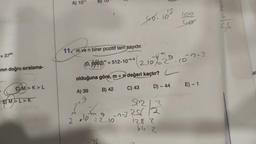
Lise Matematik
Üslü İfadeler ve Denklemler= 3724
nın doğru sıralama-
CM>K>L
EM>L>K
A) 10¹¹
e
11. mven birer pozitif tam sayıdır.
m
(0, 0002) = 512-10--3
2
B) 42
olduğuna göre, m + n değeri kaçtır?
A) 39
C) 43
Tr
45.103
-4m 9
10 = 2.10
J
2.10%/ 20.102-
51213
-2-32562
128 2
64.2
D) - 44
102
yo
E) - 1
2
6
56
as

Lise Matematik
Üslü İfadeler ve Denklemler11/
4.
Kırmızı, beyaz ve mavi üçgenler kullanılarak şekildeki gibi
bir süsleme yapılmıştır.
Süslemedeki her kırmızı üçgen içerisine 2715 yazılmıştır.
2.45
Süslemedeki her mavi üçgen içerisine 243⁹ yazılmıştır.
Süslemedeki her beyaz üçgen içerisine 8111,25 yazıl-
mıştır.
Süslemedeki bütün üçgenler içerisine yazılan sayı-
ların toplamı 4.925 olduğuna göre, kırmızıya boyanan
kaç üçgen vardır?
A) 81 B) 243
23 50
3 45
C) 339
D) 486 E) 522
3
LL
25

Lise Matematik
Üslü İfadeler ve Denklemler10.
4
4
4
4
4
4
4
3
3
3
3
4
3
2 2
2
1
2
4
2
D) 10000
4
3
2
2
2
3 3 3
4 4 4 4 4
3
4
3
4
3 4
4
3 4
3
3 4
4
4
4
Şekilde nxn birim kareden oluşan tablonun bir parçası göste-
rilmiştir. Ardışık sayma sayıları sırasıyla merkezdeki kareden
başlanarak şekilde verilen düzende bu tabloya yazılmıştır.
Buna göre, 101 sayısının yazılı olacağı kaç kare vardır?
A) 400
B) 600
C) 800
E) 10404

Lise Matematik
Üslü İfadeler ve Denklemlereis
Yayınlan
ÖRNER (03
Bir sınıfta yapılan etkinlikte sınıftaki beş kişi kare şeklinde-
ki fotoğrafları her birinden büyüterek bu fotoğrafları farklı
boyutlardaki kare posterlere dönüştürmüşlerdir. Aşağıdaki
tabloda kişilerin fotoğraflarının ve posterlerinin bir kenarla-
rının uzunlukları verilmiştir.
Damla
Ayfer
Metin
Çetin
Melih
Fotoğraf (mm) Poster (mm)
55
26
273
257
44
105
45
96
6254
124
Buna göre, poster oluşturmak için hangi kişinin fotoğ-
rafına uyguladığı büyütme oranı en büyüktür?

Lise Matematik
Üslü İfadeler ve Denklemler5.
3. Bölüm
Test 31
Tarama Testi - Ill
G
x metre
Yukarıdaki çöp kovası ile taş arasındaki mesafe
4√5 m den fazla 7√2 m den az olacak şekilde bir tam
sayı değeridir.
Çöp kovası ile taş arasında bulunan bir eni önem-
senmeyen kedinin çöp kovasına olan uzaklığı
4 metre olduğuna göre, taşa olan uzaklığı kaç
metredir?
A) 3
B) 4
C) 5
D) 6
E) 7

Lise Matematik
Üslü İfadeler ve Denklemler1,
B
8. Aşağıdaki şekilde, sekiz tane cisim üzerindeki A, B, C, D, E, F,
G ve H harfleri birbirinden farklı birer pozitif tam sayıdır.
Gom
A
B
D
• Cisimlerin üzerinde bulunan harfler kg türünden ağırlık mik-
tarlarını göstermektedir.
A) 164
• Bu cisimlerden istenildiği kadarı seçilip ağırlık miktarları top-
landığında 1'den 255'e kadar (1 ile 255 dahil) tüm pozitif tam
sayılar elde edilebiliyor.
G
Örneğin, A ve B harfli cisimler seçildiğinde elde edilen ağırlık
A + B toplamıdır. A, B ve C harfli cisimler seçildiğinde elde edi-
len ağırlık A + B + C toplamıdır.
B) 208
H
Buna göre, bu cisimlerden herhangi üçünün kg cinsinden
ağırlıkları toplamı en çok kaçtır?
C) 224
D) 288
E) 448

Lise Matematik
Üslü İfadeler ve Denklemler4. Yarıçapır olan çemberin çevresi 2πr formülü ile hesaplanır.
Şekilde 136 cm kablo ile sarılmış 6 cm iç yarıçaplı bir
makara görseli verilmiştir.
60
B
Kablo makaranın B noktasından sarılmaya başlanmış ve
A noktasında bitmiştir. Kablonun makaraya sarımı tek sıra
halinde yapılmış ve herhangi bir şekilde üst üste gelme-
miştir.
Buna göre, makaranın A noktası ile B noktası arasın-
daki yayı gören merkez açının ölçüsü kaç derecedir?
A) 90° B) 105° C) 120° D) 135°
E) 150°

Lise Matematik
Üslü İfadeler ve DenklemlerÖrnek - 9
n kenarlı bir çokgen içine yazılan sayı ile, o sayının n'ye olan
uzaklığı ifade edilmektedir.
Buna göre,
+6=37
eşitliğini sağlayan x değerleri çarpımı kaçtır?
A)-20
B)-16
C) -11
D) 6
Çözüm
E) 18

Lise Matematik
Üslü İfadeler ve DenklemlerM
115
Su yüzeyinde 1 m³ suda bulunan X mikroorganizması-
nın sayısı 9.1050 dir. Su derinliği her 1 metre arttığında
X mikroorganizmasının sayısı % 10 azalmaktadır.
Buna göre, 16 metre derinlikte 1 m³ suda bulunan
X mikroorganizmasının sayısı kaçtır?
1040
A) 332.1034
B) 334.1032
D) 3034
C) 9020
E) 3036 metrede
10

Lise Matematik
Üslü İfadeler ve DenklemlerN/
22.
ya
23.
2a + ¹ = (10)a+2
(2⁰ = 3
olduğuna göre, 5ª 4b kaçtır?
D) Yalnız I
g
9
9
A) 250 B) 100 C)
59.3
FB.
ati
P
= S
a = 2* - 1
b = 3x
+ Sa+²
E) Yalnız
9
50
7
27
- 29+2
eb
9
D) -7/0
10
2
2
E) 3
8
=g

Lise Matematik
Üslü İfadeler ve DenklemlerPapatya Anaokulunun 4 yaş grubunda 4 çift ikiz öğrenci var-
dır. Sınıf öğretmeni yapılacak bir etkinlik için öğrencileri ikiz
öğrenciler aynı grupta olmamak şartıyla 4 er kişilik iki gruba
ayırmak istemektedir.
Gruplardan birine boyama diğerine de kesip yapıştırma
etkinliği yaptırılacağına göre, öğrencilerin seçimi kaç
farklı şekilde yapılabilir?
23
A) 12
B) 16
C) 24
D) 36
E) 48

Lise Matematik
Üslü İfadeler ve Denklemler9.
2
2
(7.2) (7.3). (7.2²) ²6
A = 14² +212 +28²
olduğuna göre, A sayısının asal çarpanlarının toplamı
kaçtır?
A) 56
7 ((2²). (3)² (12²))
1. C
2. B
Sulgemale
B) 49
3. B
C) 40
4. D
9100 spupublo
D) 38
5. D
E) 36
6. C
66
24
12.
7. D
