Üslü İfadelerde İşlemler Soruları

İKİNCİ DERECEDEN DENKLEMLER ? ÖRNEK Aşağıda akıntısı olmayan bir nehir görseli verilmiştir. C(Cenk) Mater katkis karey görelin Harez rak as x+1 x + 5 AlAydin) C noktasında bulunan Cenk düşey bir biçimde D noktasına yü- zerek gittiğinde AB yolunun 1 km eksiği kadar yüzdüğünü gör- müştür. Cenk karaya çıktıktan sonra CD yolunun 2 km eksiği kadar yol giderek B noktasına ulaşmıştır. A noktasında bulunan Aydın ise B noktasına kadar yürüyüp B noktasından kayığa binerek yürürken aldığı yol kadar kayıkla giderek C noktasına varmıştır. Buna göre, AB mesafesini tam kareye tamamlama yöntemi ile bulunuz. (A, B, D doğrusal) x² + -2) x² +10 x2 + 5x şeklind x² ) (x= (x+1) çözüm x +X-ux th=x+2x+1 x²6x+3=0 (x-760 ACIL MATEMATIK Harezm pozitif k IX-1 VES A X B X-3 Yukarıd tirip ikin ve kökle ISPAT a v ax+ b (x - 1)² + (x-3)² = x² * - 2x + 1 + x2 - 6x + 9 = x x2 - 8x + 10 = 0 (x-4)² – 6=0 (x-4)² = 6 x - 4 = 6 veya x-4 = -6 x = 4 + V6 veya x = 4 - 6 X-3 > 0 ise x> 3 olması gerektiği için x = 4 + 6 olmalıdır. al x2+ *2 + b X + 2a b X+ 2a

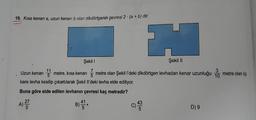
19. Kısa kenarı a, uzun kenarı b olan dikdörtgenin çevresi 2 · (a + b) dir. Şekil Şekil 11 7 5 5 kare levha kesilip çıkartılarak Şekil II'deki levha elde ediliyor. Uzun kenarı 13 metre, kısa kenarı 5 metre olan Şekil l'deki dikdörtgen levhadan kenar uzunluğu 3 10 metre olan üç Buna göre elde edilen levhanın çevresi kaç metredir? A) 27 5 B) C) c 43 5 D) 9

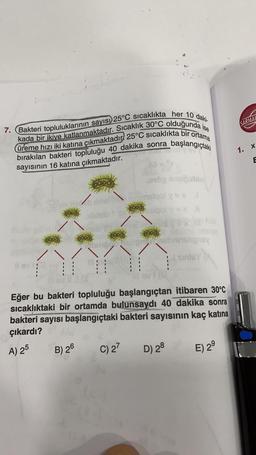
SARMAL 7. Bakteri topluluklarının sayısı) 25°C sıcaklıkta her 10 daki. kada bir ikiye katlanmaktadır. Sıcaklık 30°C olduğunda ise üreme hızı iki katına çıkmaktadır. 25°C sıcaklıkta bir ortama bırakılan bakteri topluluğu 40 dakika sonra başlangıçtaki sayısının 16 katına çıkmaktadır. 1. X E 100 ubio 6300 til delovala on py sinley H: Eğer bu bakteri topluluğu başlangıçtan itibaren 30°C sıcaklıktaki bir ortamda bulunsaydı 40 dakika sonra bakteri sayısı başlangıçtaki bakteri sayısının kaç katına çıkardı? B) 26 C) 27 E) 29 A) 25 D) 28

ÖSYM Örnek:13 Aşağıdaki tabloda bazı varlıkların kütlelerinin kilogram cinsin- den yaklaşık değerleri verilmiştir. Kütle (kg) 2x1030 6x1024 Varlık Güneş (G) Dünya (D) Köpek Balığı (K) İnsan () Bakteri (B) 5x103 7x101 1x10-15 9x10-31 Elektron (E) ve oranları arasındaki sırala- Di G K B Bu tabloya göre; E malardan hangisi doğrudur? G K B K GB K BG A) B) C) D I E D i ED BGK B KG D) E) E i D (2017/ÖRNEK TYT) E Di

Örnek: 9 Yan yana kutular kullanılarak aşağıdaki şekil oluşturuluyor. En soldaki kutuya 8 ve bir sonraki kutuya solundaki kutunun içindeki sayının 4 katı yazılarak tüm karelerin içine sayılar yazılı- yor. 299 8 . En son kutuya 299 yazıldığına göre, şeklin ortasındaki kutu- nun içine hangi sayı yazılmıştır? B) 817 C) 252 A) 425 D) 649 E) 1615

internet üzerinden yapılan 6 turluk bir yarışmanın ilk turuna 1.000.000 yarışmacı katılıyor. Her turun sonunda, o tura katılan yarışmacıların 5'te 1'i ele- niyor ve sadece kalan yarışmacıların tamamı bir sonraki tura katılıyor. Buna göre, 6. turun sonunda kalan yarışmacı sayısı kaçtır? A) 216 B) 218 C) 220 D) 222 E) 224

A A TYT / TEMEL MATEMATIK 5. Arif'in elinde 5 TL'lik, 10 TL'lik ve 50 TL'lik kâğıt paralar- dan yeteri kadar bulunmaktadır. Arif her kâğıt para türünden en az birer tane verecek şekilde 145 TL'lik bir ödemeyi kaç farklı şekilde ya- pabilir? A) 11 B) 12 C) 13 D) 14 E) 15

3. Bir proje için Türkiye'nin 81 ilinin her birinden x tane okul belirlenmiş ve her okulun müdürüne bir mesaj gönderilmiştir. Sonra, her okulun müdürü de bu mesajı okulundaki 35 öğretmene göndermiştir. Bu mesajın gönderildiği müdür ve öğretmenlerin toplam sayısı 66 olduğuna göre, x kaçtır? A) 32 8:42 C) 52 D) 62 E) 72

Her bir ürünu top- lamda 672 lira kâr elde ettiğine göre, a değeri di ha kaçtır? A) 30 B) 35 C) 40 D) 45 E) 60 7 E 14. a, b ve c pozitif tam sayılardır. + 3b + c + 7 2 X = 22a + 8 1 tant Ibtct 2 -29+2c-2 36 +36 + to G 2 y = 4+a+c-1 Z = 8b+c+2 12 -C C 2 eşitlikleri veriliyor. X y ifadesindeki x, y ve z sayılarının her biri 2 4.2 katına çıkarılırsa aşağıdakilerden hangisi elde edilir? 1 D) 1 E) 2 16 4 B) 22te c) 21% +K+S 76 +36-1-3 +/- 2 36+31+8 21

2 -2 - 8. bölüm Buna P(x) = (x - 2)n +3 - (x - 2)n +2 – 2m + 1 polinomu (x - 4) ile tam bölünebildiğine göre, m ile n arasındaki bağıntı aşağıdakilerden hangisidir? X - polina ni A) Val C) m- n = 1 A) m - n = 0 B) m + n = 1 E) m + n = 2 D) m-n=-1 E) 6 7.A 8.C 6.B 55 23

2 2x+212 5. Mehmet ve Selçuk isimli iki arkadaş arasında bir sayı tah- min oyunu oynanmaktadır. Mehmet üç basamaklı bir doğal sayı belirlemiş, Selçuk ise bu sayıyı bulmak için cevabı "Evet" ya da "Hayır" olacak şekilde aşağıdaki gibi sorular sormaktadır. 950 den küçük mü? Evet 325 ten büyük mü? Hayır 175 ten küçük mü? Evet Selçuk Mehmet Buna göre, Selçuk'un sayıyı doğru tahmin edebilmesi için sorması gereken soru sayısı en az kaçtır? A) 8 B) 9 C) 10 D) 11 E) 18

Bir futbol takımı, 2021-2022 sezonu için, biri deplasman ve diğeri iç saha olmak üzere, iki farklı forma tasarımını taraftarlara sunmuştur. Sezon içerisinde iç saha formalarının toplam satış adedi 1'den 54 e kadar olan tam sayıların toplamına, deplasman formalarının toplam satış adedi ise 1'den 54 - 1'e kadar olan tam sayıların toplamına eşit olmuştur. e Buna göre, toplam kaç adet forma satılmıştır? A) 55 B) 58 C) 510 D) 512 E) 516

Bir bakteri türü her dakika 2 katına çıkarak çoğalıyor. Bir deney kabína 1 bakteri konuluyor ve bir saat sonra deney kabının tamemen olduğu görülüyor. 1 Buna göre, deney kabının ü kaç dakikada dolmuş- 4 tur? A) 10 B) 15 C) 18 D) 20 E) 58

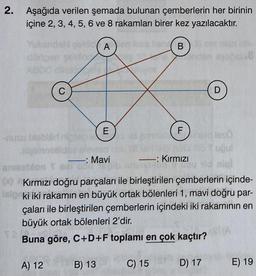
2. Aşağıda verilen şemada bulunan çemberlerin her birinin içine 2, 3, 4, 5, 6 ve 8 rakamları birer kez yazılacaktır. A B C D E F nusu olbrni dleso birine -: Mavi - -: Kırmızı or on 00 Kırmızı doğru parçaları ile birleştirilen çemberlerin içinde- ki iki rakamın en büyük ortak bölenleri 1, mavi doğru par- çaları ile birleştirilen çemberlerin içindeki iki rakamının en büyük ortak bölenleri 2'dir. Buna göre, C+D+F toplamı en çok kaçtır? A) 12 B) 13 C) 15 D) 17 E) 19

MATİK TESTİ 6 8 30xt+3 2t t+3 X ve : 224 7 olduğuna göre, x in pozitif değeri aşağıdakilerden han- gisidir? A) 8 B) 16 C) 24 D) 32 E) 64 le 58 x2+2x + 80 - 18X + X 2x ²L 16x +80 x² 8x + 40 = C X 31. 8 120°

Ü 15. 9 = 10 - 1 99 = 102-1 999 = 103_1 9999 = 104 - 1 11 = 10 + 1 101 = 102 + 1 1001 = 103 + 1 10001 = 104 + 1 : : : miştir. eşitlikleri veriliyor. 12 999...9 1000...1 A= m2 (+1) basamaklı basamaklı A sayısı 60 basamaklı bir sayı olduğuna göre, m sayısının rakamları toplamı kaçtır? D) 8 A) 3 C) 6 E) 12 B) 4