Lise Matematik Soruları
TYT, AYT, YKS, LGS, KPSS, ALES hazırlık sürecinde dilediğin dersten soru çözüm desteği almak ister misin? Kunduz’a sorularını sor, alanında uzman eğitmenler cevaplasın.

Lise Matematik
Sayı Problemleri2.
daß die ander
E) ¹4
A)3
Bir araç A ile B noktaları arasındaki yola a km/s
hızla gidip b km/s hızla dönüyor.
Gidiş-dönüş toplam c saat sürdüğüne göre,
A ve B noktaları arasındaki yol uzunluğunun
a, b ve c türünden eşiti aşağıdakilerden han-
gisidir?
A) a-b
C
D)
C) 4
a b c
C + 1
B)
a.b.c
a+b
E)
c) a +
C
a.b.c
2
Bir bisikletli A'dan B'ye saatte 20 km hızla gidip hi
durmadan saatte 30 km hızla geri dönüyor.
Buna göre, bisikletlinin bu gidiş dönüşteki o

Lise Matematik
Koşullu Olasılık25. 7 erkek 4 kız öğrenci olan bir sınıfta öğretmen bu
öğrencilerden biri olan Hakan'a "İçinde senin olmadığın,
en az biri kız öğrenci olan ve 3 öğrenciden oluşan bir ekip
kur." demiştir. Hakan, öğretmenin söylediği "en az bir kız
öğrenci olsun." şartını "en az bir erkek öğrenci olsun."
biçiminde yanlış hatırlayıp ekibi buna göre kurmuştur.
Buna göre, Hakan'ın kurduğu ekibin öğretmenin isteğine
uygun olmama olasılığı kaçtır? A 0654,

Lise Matematik
Karışım Problemleri1. Ayşe ve Aslı kardeşler evde içecek yapmak istiyorlar. Aslı
şeker oranı %15 olan 80 gr'lık bir içecek hazırlar. Ayşe
ise şeker oranı %30 olan 160 gr'lık başka bir içecek ha-
zırlarlar. İkisi de içecekleri denediklerinde beğenmezler
ve birbirine karıştırdıklarında tadının daha güzel olacağını
düşünürler. İki kardeş içecekleri bir kabın içinde birbirine
karıştırırlar.
Oluşan yeni karışımın şeker oranı % kaçtır?

Lise Matematik
Kesir Problemleri27. Merve bir müzik listesindeki şarkıların tamamını din-
lemek istemektedir. Listeyi dinlemeye başladıktan bir
süre sonra dinlemeyi bıraktığında dinlediği şarkı sayı-
sının dinlemediği şarkı sayısına oranının olduğunu
görüyor. Bir gün sonra 16 şarkı daha dinlediğinde bu
oranın olduğunu görüyor.
Buna göre Merve'nin müzik listesindeki şarkı sayısı
kaçtır?
A) 364
D) 440
B) 412
7
C) 436
E) 448

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri36
1^_4₁1M+ 3)
5240-12
x² + mx + m + 3 > 0
-
eşitsizliği her x ER için doğru olduğuna göre, m nin alabi-
leceği tam sayı değerlerinin toplamı kaçtır?
A) 6
B) 8
C) 10
moliment
K
2
TEST 02
1
LO
D) 12
6
f
E) 14
9.

Lise Matematik
Trigonometrik Denklemlerlir?
secx
H
Com
10. ¹<x< olmak üzere
2
11.
1 − sinx .V1 + sinx
cotx
ifadesinin en sade hali aşağıdakilerden hangisidir?
A) sinx
D) -sinx
Sn
¹<x<л olmak üzere
2
B) cosx
Isinx
siny
E) 1
C)—cosx
1-sin
Cosy
shx I-sne
cosy
Gy
sh
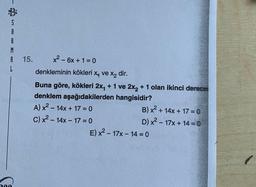
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli DenklemS
A
R
M
A
L
200
15.
x² - 6x + 1 = 0
denkleminin kökleri x ve x₂ dir.
Buna göre, kökleri 2x₁ + 1 ve 2x2 + 1 olan ikinci derece
denklem aşağıdakilerden hangisidir?
A) x²14x + 17 = 0
C) x²14x-17-0
B) x² + 14x + 17=0
D) x² - 17x + 14 = 0
E) x² - 17x - 14 = 0

Lise Matematik
Sayı ProblemleriA
23. Sinem ile kardeşi Erol aralarında aşağıdaki oyunu
oynuyorlar.
ilk olarak Sinem iki basamaklı bir doğal sayı söyledikten
sonra Erol bu sayının her basamağındaki rakam için
•
tek ise bu rakama 1 ekleyip elde ettiği sayının
yarısının 6 fazlasının rakamları toplamını bu
basamağa,
• çift ise bu rakamın yarısına 9 ekleyip elde ettiği
sayının rakamları toplamını bu basamağa
gelecek biçimde yeni bir sayı söylüyor. Daha sonra
Sinem bu sayıya aynı işlemi uygulamaya devam edip
yeni bir sayı söylüyor. Bu şekilde oyuna sırasıyla devam
ediyorlar.
Örneğin, Sinem'in söylediği ilk sayı 23 ise Erol'un
söylediği sayı 18, Sinem'in söylediği sayı 74,... olur.
Oyuna ilk olarak Sinem 43 sayısını söyleyerek başlıyor.
Buna göre, rakamları aynı olan ilk sayıyı söyleyeni
ve bu sayı aşağıdaki seçeneklerin hangisinde
verilmiştir?
A) Sinem, 22
C) Erol, 55
Sinem
43
E) Sinem, 11
B) Erol, 66
D) Sinem, 44

Lise Matematik
Türev Alma Kuralları4
urevi
8
RUM
18.
B) 36
Pigun)
AYT102122
f(x) = ex-4
g(x) = 4 + 3-Inx
olduğuna göre, (fog)(x) in x = 4 apsisli noktasındaki
teğetinin eğimi kaçtır?
A) 32
9(4)
ljet
4+3/09/4/2
78
C) 48
IN
D) 64
126
E) 96
log
-3
13
21. x pa
oldu
A) 1

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerine-
{4}
ģi
6)
SESEN YAYINLARI
11. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
X
A) 6
-3
-3
-1
-145
BT
f(x-2)
Buna göre,
≥ 0 eşitsizliğini sağlayan x'in ala-
f(-x) we 3
bileceği birbirinden farklı tam sayı değerlerinin topla-
mı kaçtır?
2
y
4
O
5
C)
3
-x-X+X+ * = 6
y = f(x)
D) 10
E) 12
2.

Lise Matematik
Aralık Kavramı34
D(0,105)
A(0,70)
MATEMATİK
B(60,0)
1-
Dik koordinat düzleminde verilen ABO üçgen ve ABCD
dörtgeni biçiminde modellenmiş havuzların alanları birbi-
rine eşittir.
C
129
A(0, 70), B(60, 0), D(0, 105) olduğuna göre C nokta-
sının koordinatları toplamı kaçtır?
m
A) 70
B) 75
Ooo
C) 80
X
D) 85
S
E) 90

Lise Matematik
İşçi Problemleri 21. Bir pastanede çalışan Sergen ve Demet'in bir A tipi ve
bir B tipi pasta hazırlama süreleri dakika türünden
aşağıdaki tabloda verilmiştir.
Sergen
Demet
A tipi
hazırlama
süresi
40
25
B tipi
hazırlama
resi
30
40
Bu pastane, 8 tane A tipi ve 10 tane B tipi pasta siparişi
alıyor. Siparişi aldıktan sonra; Sergen ile Demet bu
pastaları hazırlamaya başlıyor. Her bir pastanın
yapımında sadece bir kişi çalışacaktır.
Buna göre, Sergen ile Demet'in bu pasta siparişini
hazırlaması en az kaç dakika sürer?
A) 260
B) 270
C) 280
D) 290
23. Sine
oyn
22.9
E) 300
İlk
SO

Lise Matematik
Hareket Problemleri7.
Temel Matematik Testi
A
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A
Yukarıdaki görselde her biri 1 birim uzunluğunda olan 40 bölmeli bir tüpün A ve B uçlarından sırasıyla K ve L gazian ekte g
mektedir. Gazların ilerleyiş hızları (V) ile ağırlıkları (M) arasında
M₁
VK
VLVMK
VL
ilişkisi vardır.
Ağırlığı 6 gram olan K gazı tüpün A ucundan, ağırlığı 96 gram olan L gazı ise tüpün B ucundan aynı anda enjekte ediliyor.
Buna göre, bu iki gaz kaç numaralı bölme çizgisinde karşılaşır?
A) 8
B) 12
C) 24
D30
9. Deneme
96
6
MK
16 < x 225
B
E) 32
9616
36
16
96

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar8.
v.com.tr
işleminin
A) 1
sonucu kaçı
B) 5
log332/
B
C) e5 D) e6
B) 4
A
/30%
log281
Yukarıdaki ABC üçgeninde; IABI= log₂32 birim,
IACI = log₂8 i birim ve m(BAC) = 30° dir.
Buna göre, A(ABC) kaç birimkaredir?
A) 5
C) 3
D)
5
C
2
E)
E)
5
4

Lise Matematik
Sayı Kümelerine Giriş16. x, y ve z farklı asal sayılar olmak üzere,
A = xa.yb.zc
sayısının (a + 1)(b + 1)(c + 1) tane pozitif tam sayı
böleni vardır.
yae nin
Buna göre, 22² + 332 sayısının kaç tane pozitif
tam sayı böleni vardır?
C) 6
A) 3
B) 4
123
EABB
2
22
D) 8 E) 12
4
5 6 7 8 9 10 11 12 13 14 15 16
CADBB DDECCDC
• 33² = (2+1). (2+1)
3.3

Lise Matematik
Fonksiyonun Grafiği9. Bir öğretmen yaş problemlerini anlattık-
tan sonra öğrencilerine aşağıdaki soru-
yu sormuştur:
"Ben, eşimin üniversiteye başlamasın-
dan 2 yıl önce üniversiteden mezun ol-
dum. Eşim ise ben üniversiteye başla-
op dıktan 12 yıl sonra üniversiteden mezun
oldu. Ayrıca eşim ve benim üniversiteye
başlamamız ile mezun olmamız arasın-
da geçen süre eşittir. Buna göre, eşimin
üniversiteye başlaması ile mezun olma-
sında geçen süre kaç yıldır?”
010
Buna göre, öğrencilerin soruya ceva-
bi kaç olmuştur?
A) 3
B) 4
A5
5 D) 6
E) 7
49
