Asal Çarpanlar ve Tam Bölenler Soruları

Lise Matematik
Asal Çarpanlar ve Tam BölenlerAB iki basamaklı bir doğal sayı olmak üzere,
AB: "AB sayısının farklı asal çarpanlarının toplamı" biçi-
minde tanımlanıyor.
Buna göre, KL = 8 şartını sağlayan kaç tane KL iki
basamaklı doğal sayısı vardır?
A) 2
B) 3
SCA
C) 4
UA
D) 5
E) 6

Lise Matematik
Asal Çarpanlar ve Tam Bölenler1. n kenarlı bir çokgen ile bu çokgenin içine yazılan sayıdan olu-
şan ifade, çokgen içindeki sayı ile çokgenin kenar sayısının çar-
pımınından büyük olan en küçük asal sayıya eşit olarak tanım-
lanıyor.
Örnek: 5-7 = 35 tir. 35 ten büyük en küçük asal sayı 37 ol-
duğundan,
7
= 37 olur.
Aşağıda iki farklı eşitlik veriliyor.
3 = X ve
x-5 = y
olduğuna göre, y kaçtır?
3. Aşa
için

Lise Matematik
Asal Çarpanlar ve Tam Bölenler6. İki pozitif tam sayının 1'den başka ortak böleni
yoksa bu sayılar aralarında asaldır.
Mehmet Bey mağazasında sattığı kolonyanın
fiyatına bir sonraki ay zam yapacaktır. Kolon-
yanın zamlı satış fiyatı, şimdiki satış fiyatı ile
aralarında asal olan ama kendisi asal sayı
olmayan TL cinsinden bir tam sayı olacaktır.
Görselde kolonyanın şimdiki satış fiyatı
verildiğine göre yapılacak zam en az kaç
TL olabilir?
A) 1
B) 5
18
C) 7
D) 11

Lise Matematik
Asal Çarpanlar ve Tam Bölenlerr, m ve n pozitif
tır?
E) 10
2. VIDEO
6.
ve
birbirinden farklı asal sayılardır.
Buna göre,
AF
sayısının pozitif tam sayı bölen sayısı kaçtır?
A) 12
B) 20
D) 36
C) 24
7+5-
E) 40
4 VIDEO
destek serisi
43

Lise Matematik
Asal Çarpanlar ve Tam Bölenler1. Pelin 1 den 100 e kadar olan sayıları, "Her grupta, o gruptaki
sayıların her birine tam bölünen bir sayı bulunur." kuralına göre
gruplandırıyor.
Örneğin; bir gruptaki sayılar 1, 2, 3, 4, 6 ve 12 olabilir, çünkü
12 sayısı bu gruptaki sayıların her birine tam bölünür.
Buna göre, Pelin'in oluşturduğu bir grupta en fazla kaç sayı
bulunabilir?
A) 10
B) 11
C) 12
D) 15
E) 16

Lise Matematik
Asal Çarpanlar ve Tam BölenlerÖrnek 8:
a bir sayma sayısı olmak üzere,
5ª +5ª +5ª +
+5a
48 tane
***
48.52
sayısının pozitif çift bölen sayısı 96 dır.
Buna göre, a kaçtır?
A) 7
B) 8
C) 9
D) 10
kaf
E) 11
Çıkmış
Bir Ad
12
.
.
70
Bun
kam
A)

Lise Matematik
Asal Çarpanlar ve Tam Bölenleroplamı
2
Sile-
Asal çarpanlara ayırma konusunu açıklamak için bir öğren-
ci taç yapraklarını kullanarak aşağıdaki gibi çiçek modelleri
hazırlamaktadır.
7
7=7
7 taç yaprak
24
24 = 2x2x2x3
9 taç yaprak
21
21 = 3 x 7
10 taç yaprak
Bu modellerde, modeli hazırlanacak sayı merkeze yazıl-
makta; daha sonra o' sayının asal çarpanları belirlenmekte-
dir. Sonra, asal çarpanın değeri kadar taç yaprak yan yana
konulmakta ve böylece şekildeki gibi çiçek modeli oluşturul-
maktadır.
Bu öğrenci, 2 den 101 e kadar olan 100 doğal sayının bu
yöntemle çiçek modellerini oluşturuyor.
C) 5
Buna göre, bu modellerden kaç tanesinde 11 adet taç
yaprak kullanılmıştır?
A) 3
B) 4
D) 6
E) 8
54

Lise Matematik
Asal Çarpanlar ve Tam Bölenler330 cm
510 cm
Yukarıdaki 330 cm ve 510 cm uzunluğunda olan iki ha-
lat, hiç artmayacak şekilde mümkün olan en büyük ve eşit
uzunlukta parçalara ayrılıyor. Bu parçaların her biri ile aşa-
ğıdaki çemberler yapılıp aralarında boşluk bırakılmadan
yan yana konuyor.
x cm
Buna göre bu çemberlerin çap uzunlukları toplamını
ifade eden x kaç cm'dir? (= 3 aliniz.)
M.8.1.1.2
A) 250
B) 260
C) 270
Sausal wounce minimetel a +
LARISADIK UYGUN YAYINLARI SADIK UYGUN YAYINLARI SADIK UYGUN YAYINLARI SADIK UYGUN YAYINLARI
nad nebyello
D) 280
3

Lise Matematik
Asal Çarpanlar ve Tam Bölenlercm'lik
ruma
E) 10
1
U
1. Bir
miktar kolonya her şişede 300 ml kolonya olacak şekil-
de doldurulduğunda 120 şişe kullanılıyor.
Buna göre, bu kolonya her şişeye 250 ml olacak şekil-
de doldurulursa kaç şişe kullanılmalıdır?
A) 135
B) 144
C) 150
D) 156
E) 160

Lise Matematik
Asal Çarpanlar ve Tam Bölenler#. A = 2*.3*.7 olduğuna göre, A sayısını tam bölen-kaç
farklı çift tam sayı değeri vardır?
> bir tono en oz 2'y
Cilardim
?
A) 24
B) 40.
C) 64
7116
qy
232
3
BO
ferr
4.5.2 = 40
E) 96
Bu posty besten for
=40 40 tone

Lise Matematik
Asal Çarpanlar ve Tam BölenlerAsal çarpanlarına ayrıldığında her bir asal çarpa-
nının kuvveti 1 olan sayılara "karesiz sayı" denir.
Örneğin, 30 = 2¹.3¹.5¹ olduğundan 30 sayısı bir
karesiz sayıdır.
Buna göre,
I. 105 bir karesiz sayıdır.
II. İki basamaklı en küçük karesiz sayı 10 dur.
III. Dört basamaklı karesiz sayı yoktur.
ifadelerinden hangileri doğrudur?
A) Yalnız I (0/B) I ve II
D) II ve III
C) I ve III
E) I, II ve III

Lise Matematik
Asal Çarpanlar ve Tam Bölenler29+1
3
sağlayan p değerine "Wagstaff asalı" denir.
34. p ve q birer asal sayı olmak üzere,
Buna göre, iki basamaklı farklı Wagstaff asal
sayılarının toplamı kaçtır?
A) 14
05183
B) 45
C) 54
= p eşitliğini
D) 57
TE
E) 71
36
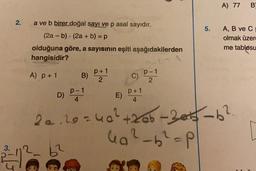
Lise Matematik
Asal Çarpanlar ve Tam Bölenler2.
a ve b birer doğal sayı ve p asal sayıdır.
(2a - b) (2a + b) = p
olduğuna göre, a sayısının eşiti aşağıdakilerden
hangisidir?
-=A
A) p + 1
3.
212
.
62
B)
p+1
2
C)
P+1
4
E)
P-1
2
5.
A) 77 B
D) P-1
4
20.20=40² +2ab-2013-b²
4₁²-b²=P
A, B ve C
olmak üzer
me tablosu

Lise Matematik
Asal Çarpanlar ve Tam BölenlerEBOB-EKOK
1. x, y ve z pozitif tam sayılardır.
A = 4x - 3= 6y-5=7z - 1 ise,
A sayısının alabileceği üç basamaklı en
küçük değeri kaçtır?
A) 181
B) 185
D) 189
C) 187
2. TEST
E) 193
4. Dai
bir
niv
sa
U
r

Lise Matematik
Asal Çarpanlar ve Tam Bölenler2.
a a sayısının en büyük asal böleni.
= a sayısının en küçük asal böleni
a
olarak tanımlanıyor.
Buna göre,
78 + 315
işleminin sonucu kaçtır?
Tipo
A) 16 B) 14
C) 12 D) 10 E) 9
5.
ens Yayınları
a
= at ve
Buna göre,
2
.
2
sayısının poziti
A) 5
B) E

Lise Matematik
Asal Çarpanlar ve Tam Bölenler. Herhangi bir sayma sayısının; 10 ile bölümünden elde edilen
kalanın alabileceği değerler toplamı A, 7 ile bölümünden elde
edilen kalanın alabileceği değerler toplamı B'dir.
M
A
B
Buna göre, oranı kaçtır?
15
A) 11/0
7
B)
C) 3
77
2
D)
E) 4
