Belirli İntegral ve Uygulamaları Soruları

32 f(x) = (x-3)2 10 Boğaziçi köprüsü, köprü ayakları ve köprü halatları ile sınırlı bölge +(x) = (x - 33 + 1 fonksiyonunun grafiği, x = 0, x= 6 doğruları ve x ekseni ile modelleniyor. Buna göre, yukarıda belirtilen sınırlı bölgenin alanı kaç br dir? A) 7,8 B)8 C)7,2 D) 8,4 E) 9

pok Metrop po typol Metropol Metropol Metropol Metropol Metropa por metropol Metropol Metropol Metropol Metropol Lopa Metropol Metropol Metropol Metropol Metropol Metropa Metropol Metropol Metropol Metropol Metrop of Metropol Metre Metropol Metropol Metro Metrop bol Metropol YÖS Soruları / Y 28 Metron opol Metropo pol Metropol Metropol Metropol Metropol //opol Metrop Oopol Metropolitropolopol Metropol Metrop opol Metropol Metropol Wetropol Metrto Metrop Pool Me Metropole Met opol Metropol Me fopol Metropol Metropol Metrop ropol Metropoitropol Metropol Metrop opopetropol Metropol tiropol Metrop topol Metropol Metropol Metropy

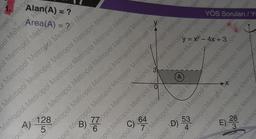
23. | [3f(x) - 2]dx = A olduğuna göre, [ f(3x - 2)dx colo integralinin A türünden eşiti aşağıdakilerden hangisidir? A-2 +2 A + 4 A) 42 (8) 9+2 CAHA A) - A-2 A + 4 E) -

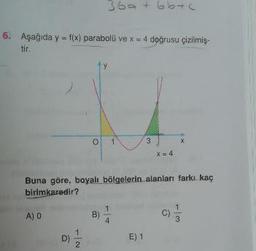
360+ obec 6. Aşağıda y = f(x) parabolü ve x = 4 doğrusu çizilmiş- tir Buna göre, bayalı bölgelerin alanları farkı kaç birimkaredir? A) O D) E)1

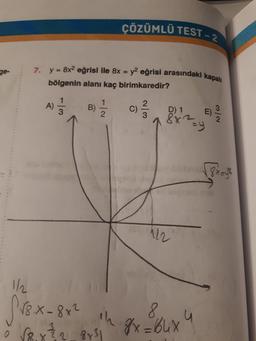
CÖZÜMLÜ TEST ge- 7. y = 8x2 eğrisi ile 8x = y2 eğrisi arasındaki kapa bölgenin alanı kaç birimkaredir? A) 5 B) 5 C) D E E 1/2 on Pr8.x- 8x2 o rex prsih 8x=64x4

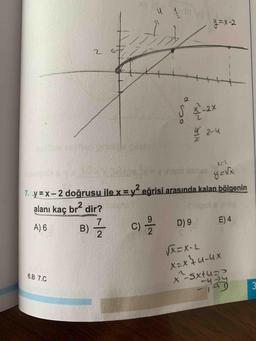
y=x-2 o - 2-4 X=2 y Ex 7. y = x - 2 doğrusu ile x = y² eğrisi arasında kalan bölgenin alanı kaç bré dir? A) 6 B) 1 C), D)9 E)4 I √x=X-2 x= x +u-ax 6.B 7.C x-sxtus

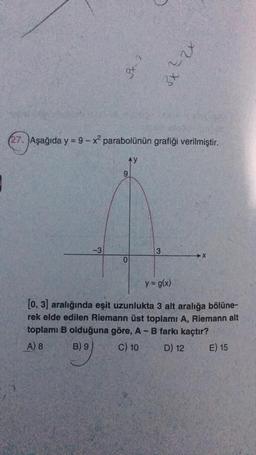
3 st 3x (27. Aşağıda y = 9 - x? parabolünün grafiği verilmiştir. AY 9 -3 3 X 0 y = g(x) [0, 3) aralığında eşit uzunlukta 3 alt aralığa bölüne- rek elde edilen Riemann üst toplamı A, Riemann alt toplamı B olduğuna göre, A-B farkı kaçtır? A) 8 B) 9 C) 10 D) 12 E) 15

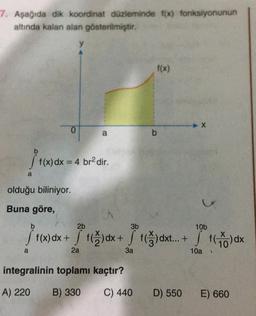
7. Aşağıda dik koordinat düzleminde f[x) fonksiyonunun altında kalan alan gösterilmiştir. f(x) 0 a b 1 (x) dx f(x) dx = 4 br2 dir. a olduğu biliniyor. Buna göre, 2b 3b 10b i f(x) dx + f(x) dx + f(Ă)dx + (3) dxt... + ) 10 a 2a 3a 10a integralinin toplamı kaçtır? A) 220 B) 330 C) 440 D) 550 E) 660

İNTEGRAL 4. ADIM GÜL du =dx A 1. ifadesi aşa Zemin a aşa- Petrol sizan bölge Ara bölge A Vx+1 x Petrol katman du du Bir petrol kuyusundaki pompa zemin altındaki petrol katmanına ulaştığında pompanın katmanla birleştiği noktadan bir süre sonra petrol sızmaya başlamıştır, Sızan petrol zemin ile petrol katmanı arasındaki ara bölgeye dağılmaktadır. Pompa çalışmaya başladıktan t süre (dk) sonunda yayıldığı alanı (m2) modelleyen P(t) fonksiyonu sü- reklidir ve 0 0 <t<1 2. d+.+2 = dup(t) = 3/5 – 3 dt 13t 3 inte s eşitliği ile verilmiştir. A) APOILMA Petrol sızıntısı pompa çalışmaya başladıktan 1 dakika sonra başladığına göre, pompanın çalış- tığı ilk 4 dakika sonunda petrolün sizdığı bölge- nin alanı kaç m2 dir? C B) 18 C) 12 D) 8 16 A) 24 12t.dt=do (+²133 + C + 3

6. Ay y = x2 y = 8 y = 2x Yukarıda gösterilen boyalı bölgenin alanı aşağıda- kilerden hangisi ile ifade edilebilir? 2=X 2X A) Idxt xdx 2 (-Jako }(E-2). - vx) C - vw ]dx | x 8 C) (x dx + 2 D) S (8 - x2)dx E) dx 2

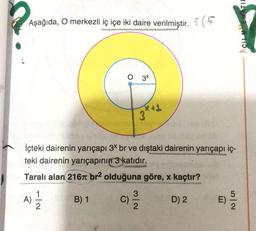
TIL Aşağıda, O merkezli iç içe iki daire verilmiştir. :( O 34 3 kg İçteki dairenin yarıçapı 3* br ve dıştaki dairenin yarıçapı iç- teki dairenin yarıçapının 3 katıdır. Taralı alan 216 br2 olduğuna göre, x kaçtır? 1 3 B) 1 C) D) 2 E) A) NW No

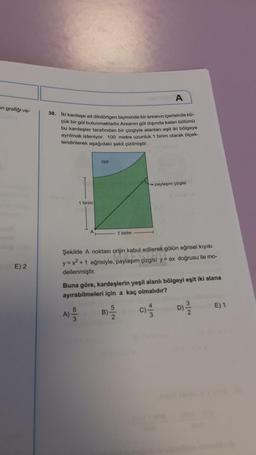
A un grafiği ve- 30. Iki kardeşe ait dikdörtgen biçiminde bir arsanın içerisinde kü- çük bir göl bulunmaktadır. Arsanın göl dışında kalan bölümü bu kardeşler tarafından bir çizgiyle alanları eşit iki bölgeye ayrılmak isteniyor. 100 metre uzunluk 1 birim olarak ölçek- lendirilerek aşağıdaki şekil çizilmiştir. Göl paylaşım çizgisi 1 birim 1 birim Şekilde A noktası orijin kabul edilerek gölün eğrisel kıyısı y = x² + 1 eğrisiyle, paylaşım çizgisi y = ax doğrusu ile mo- dellenmiştir. E) 2 Buna göre, kardeşlerin yeşil alanlı bölgeyi eşit iki alana ayırabilmeleri için a kaç olmalıdır? E) 1 D) A) B) C) Non

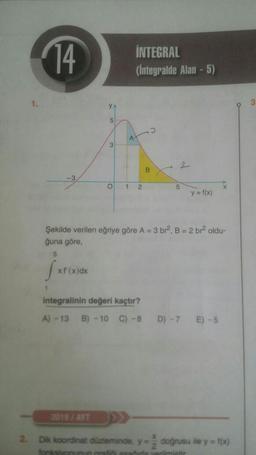
14 INTEGRAL (Integralde Alan - 5) 5 A 3 2 B. O 1 2 5 y = f(x) Şekilde verilen eğriye göre A = 3 br. B = 2 br oldu- ğuna göre, 5 ju xf'(x)dx integralinin değeri kaçtır? A) - 13 B) - 10 C) -8 D) - 7 E) - 5 2 Dik koordinat düzleminde, y dogrusu ile y=f(x) 2 verilmiatic

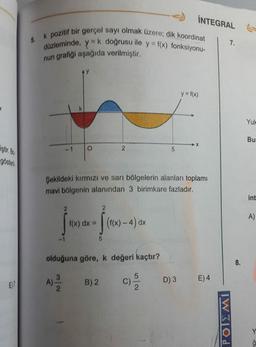
INTEGRAL 5. k pozitif bir gerçel sayı olmak üzere; dik koordinat düzleminde, y=k doğrusu ile y = f(x) fonksiyonu- grafiği aşağıda verilmiştir. 7. nun y = f(x) Yuk Bu X -1 O 2 5 göster) Şekildeki kırmızı ve sari bölgelerin alanları toplamı mavi bölgenin alanından 3 birimkare fazladır. int 2 A) f(x) dx = (f(x) – 4) dx -1 olduğuna göre, k değeri kaçtır? 8. 3 5 A) c) E) B) 2 D) 3 E) 4 2 POIZMI Y

ÖRNEK 4 4 y f(x) Yandaki grafikte [2, x] ara- lığında f(x) grafiği altında kalan bölgenin alanını veren F(x) fonksiyonu F(x) F(x) = x3 + x →X O 2 x eşitliği ile tanımlanıyor. Buna göre, f(x) neye eşittir? (4) dx = x++ =

22. -35 $ B g(x) c f(x) (x-3) + 3 = glx A Yukarıdaki dik koordinat düzleminde f(x) ve g(x) parabolleri birim kareler üzerindeki O ve A noktalarında kesişmektedir. f(x) fonksiyonu birim karelere C noktasında, g(x) fonksiyonu ise birim karelere B noktasında teğettir. Buna göre, mavi bölgenin alanı kaç birimkaredir? 4 8 16 B) 3 3 A) 3 c) 19 D) 33 E) 64 3 -1/ (x-2) ²+2 +2 = f(x)