Belirli İntegral Soruları

Lise Matematik
Belirli İntegralORİJİNAL MATEN
f(x) dx
24
X
I flex
f(a) fa
6
1
türev sefer
8. 1(x)=x²-3x -1 eğrisinin ekstremum noktalarından
geçen d doğrusunun eğri ile oluşturduğu kapalı böl-
gelerin alanları toplamı kaçtır?
A)=1/
B) - 4
C) -1/3
4
3x - 3=0
✓
@
2²-3xxx-2xx
x-x=0
D)=1/12
(1,-3)
(-4,1)
E) 1
M = U
-2x+n
2+0=
-2x-1

Lise Matematik
Belirli İntegralORIJINAL M.
8.
Jf lelax
J (9) J)
1
24
türev sefer
f (x) = x³ - 3x -1 eğrisinin ekstremum noktalarından
geçen d doğrusunun eğri He oluşturduğu kapalı böl-
gelerin alanları toplamı kaçtır?
A) = 1/2
B) -—-—-
C)=1/3
3x - 3=0
✓
0
x²-3x1--201
3 x-0
D)/
(1₁-3)
(+, 1)
E) 1
Jld
M = U
-2

Lise Matematik
Belirli İntegral12:10
f(x) fonksiyonunun grafiği aşağıda verilmiştir.
Bog
0
olduğuna göre,
1
S₁ = 13 br², S₂ = 8 br, S3 = 5.br²
3
{ 10
f(x)dx +
-5
-5
ralinin değeri kaçtır?
A)-18 B)-17
196
S3
5
f(x)
f(x) dx integ.
C) -16 D)-1 E) 1

Lise Matematik
Belirli İntegral4
S2
0
S3
2
S₁
-2
A) S3-S₁-S₂2
C) S2-S₁-2S3
Yanda verilen taralı bölgelerin alanları
sırasıyla S₁, S₂ ve S3 birimkaredir.
Buna göre,
j (f¹(lyl)- If¹(y)l) dy
-2
integralinin değeri kaçtır?
E) S3-3S2-S₁
B)-2 S₁ + S₂
D)-S₁-3S₂
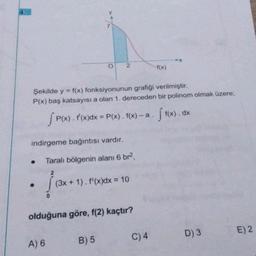
Lise Matematik
Belirli İntegralŞekilde y = f(x) fonksiyonunun grafiği verilmiştir.
P(x) baş katsayısı a olan 1. dereceden bir polinom olmak üzere;
●
O 2
indirgeme bağıntısı vardır.
A) 6
SP(X
P(x) . f'(x)dx = P(x). f(x)-a. ff(x). dx
Taralı bölgenin alanı 6 br²,
2
(3x + 1). f'(x) dx = 10
olduğuna göre, f(2) kaçtır?
B) 5
-f(x)
C) 4
D) 3
E) 2

Lise Matematik
Belirli İntegralA)
16
n çift doğal sayı olmak üzere, f(x) = xn+2 ve g(x) = x+4 fonksi-
yonlarının grafiği veriliyor.
33
f(x) ile g(x) eğrileri arasında kalan bölge A(n) olmak üzere
A(0) + A(2) +A(4) toplamının değeri kaçtır?
(C) 1/1/12
B)
O
4
y = g(x)
9
-f(x)
-X
D)
11
E)
20
33

Lise Matematik
Belirli İntegralindirgeme bağıntısı vardır.
Şekilde y = f(x) fonksiyonunun grafiği verilmiştir.
P(x) baş katsayısı a olan 1. dereceden bir polinom olmak üzere;
SP(x) . f'(x)dx = P(x) . f(x)-a. [ f(x). dx
2
A) 6
Taralı bölgenin alanı 6 br²,
2
(3x + 1). f'(x)dx = 10
olduğuna göre, f(2) kaçtır?
B) 5
-f(x)
C) 4
D) 3
E) 2

Lise Matematik
Belirli İntegral1.
K
f(x) = x³ + ax²-bx + 2
4-6-7229
^
fonksiyonu x = 1 noktasında x-eksenine teğet oldu-
ğuna göre, x-ekseni ile eğri arasındaki kapalı alan kaç
birimkaredir?
4-42-3
A)
23
4
B)
27
4
C)
32
3
-41326
D) 255
8
E)
47
4

Lise Matematik
Belirli İntegral6.
0
A) 2
y
B)
Şekilde y = -x² + 3x - 4 parabolü, x = a ve x = a + 2
doğruları ile x ekseni arasındaki kiremit döşeli bölgenin
14
alanı birimkaredir.
3
Buna göre, a kaçtır?
3
-
a
2
a+2
C) 1
7|2
18
D)=1/12
E) -1/3
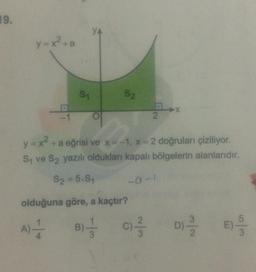
Lise Matematik
Belirli İntegral19.
y=x²+a
S₁
YA
S2
2
y = x² + a eğrisi ve x = -1, x = 2 doğruları çiziliyor.
S₁ ve S₂ yazılı oldukları kapalı bölgelerin alanlarıdır.
S₂ = 5.S₁
olduğuna göre, a kaçtır?
A) -—-
B)---
-0-1
X
C) -²/3/2
N/W
D) -3/1/2
m

Lise Matematik
Belirli İntegral。(3-4)
f(x) = -x² - 4x fonksiyonunun x ekseni boyunca sağa
doğru a birim ötelenmesi ile oluşan g fonksiyonunun gra-
fiği aşağıdaki dik koordinat düzleminde verilmiştir.
2x²-
--4x-bata
A) -8
B) -6
H
C) -4
Sanı renkli bölgenin alanı S, ve mavi renkli bölgenin
1
alanı $ arasında S₁
3-S₂ eşitliği sağlanmaktadır.
Buna göre, a³-6a² ifadesinin değeri kaçtır?
²-2ײ +69
A(x-2) = -x² - 4x
y = g(x)
D) -3
2x² + bax + a²x.
- (x-a) ²-4. (x-)
x²-2a+a²
-xx+35+92-4***
=4+9
X
E) -2
Dik koordinat düzleminde f fonksiyonunun grafiği ve-
rilmiştir.
y=f(x)
Aşağıda g
arasında
A
g(x)
eşitliği
Buna g
10
integr
A)-40
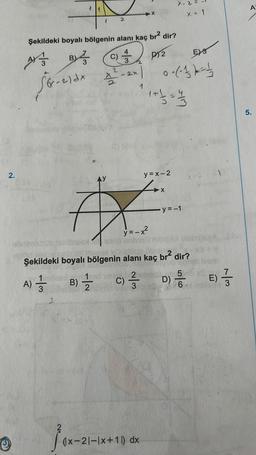
Lise Matematik
Belirli İntegral2.
Ⓡ
Şekildeki boyalı bölgenin alanı kaç br² dir?
B) 4 C)
P12
A
S&-21dx
2
2
2
2x
CISC
AY
F
DOX
y = -x²
Bottest
y=x-2
(x-21-1x+11) dx
X-2
0-1-34²-13
1 + 1/2 = 21/1/20
-X
X = 1
oladi
Şekildeki boyalı bölgenin alanı kaç br² dir?
A) //
-y=-1
ivsm
2
5
7
B) C) == 0) E
1/2
D) 6.
E) 1/3
nolias
A
5.

Lise Matematik
Belirli İntegralx ≥ 0 olmak üzere, y = 2* eğrisi, y = 2x + 2
doğrusu ve y ekseni arasında kalan bölgenin alanı
kaç br² dir?
A) 15 + log₂e
B) 15+ In2
D) 15 - 7log₂e
E-
K
11
C) 8log₂e
E) 12-log₂e
y² eğrileri arasında kalan kapalı böl
![RU BANKASI
3.
2
2. [0, 6] kapalı aralığında sürekli ve (0, 3), (3, 4), (4, 6) açık ara-
lıklarının her birinde türevlenebilir bir f fonksiyonunun türevi
olan f' fonksiyonunun grafiği aşağıdaki dik koordinat düzle-
minde verilmiştir.
2
S
D) 12,7
20
C
O
-3
3:
B) 7,3
y = f(x)
0 <c<2 olmak üzere,
f(0) = 5
olduğuna göre, f(6) değeri aşağıdakilerden hangisi olabi-
lir?
A) 5,5
4
6
E) 14,9
f(1-x) dx = 6 olduğuna göre,
C) 10,1
5](https://media.kunduz.com/media/question/seo/raw/20230208061427958104-1876695.jpg?w=256)
Lise Matematik
Belirli İntegralRU BANKASI
3.
2
2. [0, 6] kapalı aralığında sürekli ve (0, 3), (3, 4), (4, 6) açık ara-
lıklarının her birinde türevlenebilir bir f fonksiyonunun türevi
olan f' fonksiyonunun grafiği aşağıdaki dik koordinat düzle-
minde verilmiştir.
2
S
D) 12,7
20
C
O
-3
3:
B) 7,3
y = f(x)
0 <c<2 olmak üzere,
f(0) = 5
olduğuna göre, f(6) değeri aşağıdakilerden hangisi olabi-
lir?
A) 5,5
4
6
E) 14,9
f(1-x) dx = 6 olduğuna göre,
C) 10,1
5
![2.
A(-3,0) C(-1,0)|
Şekildeki AB, O merkezli dörtte bir çemberi yayı, [BC]
de B(0, 3) ve C(-1, 0) noktalarını birleştiren doğru par-
çasıdır.
A)
Buna göre, aşağıdaki integrallerden hangisi boyalı
alanı verir?
j[√9-x² - (3x + 3) dx
j1-√9->
B)
C)
D)
-3
-3
ol6 =1
S[√9-x² - (3x + 3) dx
E)
-3
[-√√9-x²-(3x+3)]dx
B(0,3)
114-³+√0-1² ov
y-3
9- y²dy
3
y-3
3
-dy +
/
0
X
9-y²dy
karekök
181](https://media.kunduz.com/media/question/seo/raw/20230208074252488477-323100.jpeg?w=256)
Lise Matematik
Belirli İntegral2.
A(-3,0) C(-1,0)|
Şekildeki AB, O merkezli dörtte bir çemberi yayı, [BC]
de B(0, 3) ve C(-1, 0) noktalarını birleştiren doğru par-
çasıdır.
A)
Buna göre, aşağıdaki integrallerden hangisi boyalı
alanı verir?
j[√9-x² - (3x + 3) dx
j1-√9->
B)
C)
D)
-3
-3
ol6 =1
S[√9-x² - (3x + 3) dx
E)
-3
[-√√9-x²-(3x+3)]dx
B(0,3)
114-³+√0-1² ov
y-3
9- y²dy
3
y-3
3
-dy +
/
0
X
9-y²dy
karekök
181

Lise Matematik
Belirli İntegral1.
Birinci bölgede; koordinat eksenleri, x = 11, y = 11 doğ-
ruları ve y = x² + 2, x = y² + 2 eğrileri arasında kalan A
bölgesi aşağıda verilmiştir.
Ay
(3,11)
TUTA
(11,3)
A bölgesinin alanı kaç birimkaredir?
A) 85
B) 80
MO
X
C) 72
UYGU
D) 70
E) 64
