Deneysel ve Teorik Olasılık Soruları

20. 1 numaralı kutuda aynı büyüklükte 2 adet sarı, 3 adet kırmızı ve 2 numaralı kutuda aynı büyüklükte 4 adet sarı, 2 adet kır- mızı top vardır. A) 1 numara Aynı anda her iki kutudan birer top alınıyor ve diğer kutuya atı- liyor. Bu işlem sonunda kutulardaki sarı ve kırmızı top sayıları- nın başlangıçtaki ile aynı sayıda olma olasılığı aşağıdaki- lerden hangisidir? IN SABT 7 15 2 numara Iepy 2 B) // C) 1/11 Il ev in D) 4 15 E) -15 22 21

nu "O- 30. - 10- Buna göre, fdx- işleminin onucu kaçtır? A)-8 f(x)dx A) 1 16 B)-4 B) C) 0 9 16 Yukarıdaki şekilde verilen A merkezli daire diliminde JAB| = 4 cm ve m(BAC) = a dir. Buna göre, daire diliminin iç bölgesinden seçilen bir noktanın A noktasına olan uzaklığının 1 cm den fazla olma olasılığı kaçtır? C) D) 4 B 15 16 C E) 4 D) 5 16 25 Diğer sayfaya geçiniz.

14. rafa gelme olasılığı A) A) —— 5 12 10 9 B) // 1 11 B) 2 U 5 16 4 5 D) 5 16 E). Ho Şekilde 8 eşit bölmeye ayrılmış sayı çarkında ortadaki ibre döndürülünce bölmelerden birinde durmaktadır. 15 Bir zar atılıyor ve sayı çarkı bir kez döndürülüyor. Buna göre, zarın ve sayı çarkının tek sayı olan bölmede durma olasılığı kaçtır? (C) 23/03 D) 1/12 8 A-3 x²=4 x = -2 Yanıt Yayınları x²-2 ² E) 16.

50J A = {3, 4, 5} B = {2, 4, 6} olduğuna göre, AxB kümesinin eleman- larını içine alan en küçük dikdörtgen ala- ni kaç br² dir? K9222 A) 2 B) 4 C) 6 D) 8 E) 10 (Spot 3'e göre) BAVA NOSA MIOYS TUVINIAVA NDAN XOYS lut G

16. Şura ile kardeşi Kağan arasında şu konuşma geçiyor: Şura: Benim babamla aramdakl yaş farkı, senin annemle arandaki yaş farkına eşittir. Kağan: Ben doğduğumda babam 33 yaşındaydı. Şura: Ben doğduğumda annem 25 yaşındaydı. Kağan'ın şimdiki yaşı 13 olduğuna göre, Şura'nın şimdiki yaşı kaçtır? A) 14 B) 17 C) 18 D) 19 E) 20 Anna

8. 21 2 a, b ve c ardışık tek sayılardır. A = {a, 3, 6, 5, b, 7, c} kümesinin tüm 3 elemanlı alt kümeleri yazılıyor. 3 elemanlı alt kümeler ile ilgili, ✓//1 tanesinde elemanlar 3'ün katıdır. II. 13 tanesinde elemanlar toplamı 3'ün katıdır. III. 21 tanesinde elemanlar toplamı çift sayıdır. yargılarından hangileri daima doğrudur? A) Yalnız I D) II ve III B) Yalnız III E) I, II ve III I ve II Diğer sayfaya geçiniz.

3. Ay müxö, ninimistale mobineb intel A) x² = y + 2 7 -2 O x-y + 4 = 0 4 2 C) x² = y +2 m x+y=4=0 -2 3 Yukarıdaki dik koordinat sisteminde aşağıdaki denklem sistemlerinden hangisinin çözümü göste- rilmiştir? -X E) x² = y + 2 18 B) x² = y - 2 x-y-4=0 VD) x² =y-2 Dublo x+y=4=0 x-y+4= 0 S(A

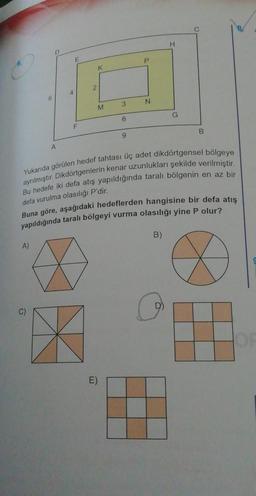
6 A) D A 4 E F 2 K M 3 E) 6 9 P N H Yukarıda görülen hedef tahtası üç adet dikdörtgensel bölgeye ayrılmıştır. Dikdörtgenlerin kenar uzunlukları şekilde verilmiştir. Bu hedefe iki defa atış yapıldığında taralı bölgenin en az bir defa vurulma olasılığı P'dir. Buna göre, aşağıdaki hedeflerden hangisine bir defa atış yapıldığında taralı bölgeyi vurma olasılığı yine P olur? A X B) G B O

Bir toplantıya katılan 5 kişiden rastgele seçilen iki kiş arasında AB kan grubuna sahip birinin bulunması ola sılığı % 90 dir. Toplantıdan 1 kişi ayrıldığında kalan 4 kişiden rast- gele seçilen iki kişinin her birinin kan grubunun AB olması olasılığı en az kaçtır? B) ²/3 3 (A) 2/1/4 (0) 1/1/12 C) 1|3 D)=1/11 X hic V en 6 (

30. Şehirler arası bir yolcu otobüsü seferlerinde 10 şe- hire uğramaktadır. Birbirinden habersiz bir şekilde bu otobüsün aynı seferinde yolculuk yapan Aslı ve Kerem'in aynı anda otobüste bulunmuş olma olasılığı kaçtır?

14. Salgın bir hastalık ilk evresinde belirti göstermemektedir. Bir kişinin bu hastalığa yakalanmış olma olasılığı 0,02 olarak hesaplanıyor. Hastalığın teşhisi için geliştirilen test; • hastalığa yakalanmış kişiye uygulandığında 0,91, • hastalığa yakalanmayan kişiye uygulandığında ise 0,04 olasılık değeri ile pozitif (+) sonuç vermektedir. Buna göre, test sonucu pozitif (+) çıkan bir kişinin hastalığa yakalanmamış olma olasılığı kaçtır? A) 14 19 B) 21 32 C) 18 29 D) 35 53 28

Aşağıda 1'den 10'a kadar numaralandırılmış yan yana duran 10 kutu verilmiştir. Bu kutuların her biri sarı, mavi veya yeşil renkler kullanılarak boyanacaktır. A) T 23 Her bir renk en az bir kere kullanılacağına göre 10 numa- ralı kutunun sarı renk ile boyanmış olma olasılığı kaçtır? C) // D) // 10 B) AHOO 4 5 6 7 8 9 10 8 3

EMEL TANIM TESTI Örnek - 25 a ve b sayma sayıları olmak üzere, (ax + b)n = n+ 1 tane Verilen kutuların içine x'in azalan kuvvetlerine göre açılımında oluşan katsayılar soldan sağa doğru yazıl maktadır. Buna göre, (ax + 2) = kırmızı kutu içindeki sayı, mavi kutu içindeki sayı- nın 3 katı olduğuna göre a + n toplamı kaçtır? 1 10x/0,8 = 500-10-3 ax=3 Örnek - 26

13. √12 cm √12 cm A) 9 √27 cm B) 8 √27 cm Yukarıda üç farklı kare ve kenar uzunlukları verilmiştir. Buna göre, bir kenar uzunluğu 75 cm olan bir kare içi- ne mavi, kırmızı ve siyah karelerden en az bir tane ko- nulması şartıyla en az kaç tane kare konulabilir? C) 7 √3 cm D) 6 √3 cm E) 5 15. 25 bina 3 4 Bu d langr A) 8

₂X - X 7 shark 03 15. Aşağıda, kenar uzunlukları 1 birim olan kare biçi mindeki dört kartonun bazı köşelerinde bulunan mavi renkli eş ikizkenar dik üçgenler şekildeki gibi. gösterilmiştir. Her bir karton, yeri değiştirilmeden kendi merkezi etrafında döndürüldükten sonra kenar uzunluğu 2 birim olan bir kare oluşturacak biçiminde kar- tonlar birleştirilecektir. Buna göre, oluşturulan bu karenin merkezin- de mavi renkli yeni bir kare oluşma olasılığı kaçtır? 3 64 A) B) 3 32 C) 32 D) 1/6 E) 16 16

PEKİŞTİRME TESTİ Şekildeki küpün köşelerinden rastgele seçilen iki tanesi- nin cisim köşegeni oluşturma olasılığı kaçtır? C) // E) -—-/- B) A) 128) D) 41 - 100 8 10 16 tane 1 birimkarelik kare her birinin üst yüzünde S, A tadır. Bu 16 kareyle 16 biri her satır ve her sütuna ya döşenecektir. (Yerleştirilecek harfler, oku Fayanslar döşendiğinde olasılığı kaçtır? (Kelime üstten alta veye a 36 A) 3 B) 108 (4) (3) 13) H