Fonksiyon Kavramı ve Gösterimi Soruları

Lise Matematik
Fonksiyon Kavramı ve Gösterimi14. f: R → R ye herhangi bir fonksiyondur.
Buna göre, g(x) = f(x) – f(-x) fonksiyonu için
1. Sabit fonksiyondur.
Tek fonksiyondur.
III. Çift fonksiyondur.
jo. II.
z?
ifadelerinden hangisi daima doğrudur?
A) Yalnızl
B) Yalnız 11
C) Yalnız III
D) I ve II
E) II ve III

Lise Matematik
Fonksiyon Kavramı ve Gösterimi3=2attha
7.
k gerçel sayı olmak üzere
a
f(x) = (x - k)2 -K?
olduğuna göre,
x ²-2xl -
f(x + k) = f(k 2
eşitliğini sağlayan kökler ile ilgili aşağıdakilerden
hangisi doğrudur?
k²
GAP Dşit iki kök vardır
B) Ters işaretli iki farklı kök vardır.
C) Aynı işaretli iki farklı kök vardır.
D) Kökler toplami pozitiftir.
E) Kökler çarpımı negatiftir
.
-kh
in
(x+2) = 2k1

Lise Matematik
Fonksiyon Kavramı ve Gösterimi7.
Her x reel sayısı için sürekli olan f, g ve h fonksiyonları
veriliyor,
f çift, g ve h tek fonksiyondur.
f(1) = 0, f(4) = 2, f(3) = 6
g(1) = -1, g(-2) = 4, g(5) = 3
-skin-A n(1) = 2, h(3) = 2, h(6) = 3
olduğuna göre,
07201
g-'(h(f(-3))) + n(f(g(-1))) + f(g(h(1)))
işleminin sonucu kaçtır? 2
23
A) 7 B)-2 C) 1
D) 5
(2) 7
1
2
12.

Lise Matematik
Fonksiyon Kavramı ve GösterimiTIK
3. f: R →R olmak üzere,
f(x) = 4x – 20
fonksiyonunun pozitif değerli olduğu en geniş aralık aşa-
ğıdakilerden hangisinde doğru olarak verilmiştir?
A) (0,5)
B) (-00,5) C) (5, )
D) (-5, 0) E) (-00,-5)

Lise Matematik
Fonksiyon Kavramı ve Gösterimi5.
f fonksiyonu her x E (0, 3) için
f(x) = 2x + 1
biçiminde tanımlanıyor ve her x gerçel sayısı için
f(x) = f(x + 3)
eşitliğini sağlıyor.
Buna göre, f(6) + f(7) + f(8) toplamı kaçtır?
A) 8 B) 12 C) 15 D) 18 E) 21
2016/LYS

Lise Matematik
Fonksiyon Kavramı ve Gösterimi4.
x= x3
14. Uygun koşullarda tanımlı ffonksiyonu için,
f(-x) = -f(x)
f(1) = 3
eşitlikleri veriliyor.
f fonksiyonunun grafiği A(-1, m - 2) noktasından
geçtiğine göre, m kaçtır?
A) 2 B) 1 C) D)-1 E)-2
f(0) = 6
g(0) = 2
cm
olduğuna gö
en hangisidir?
-E) x²
A)
A
E)x
88
6
B
C 7
E
C
12 C 13 A 14 D
9
8
A 10 E 11

Lise Matematik
Fonksiyon Kavramı ve Gösterimi1260
A
A
18. Gerçek sayılar kümesi üzerinde f fonksiyonu, a bir
tam sayı olmak üzere,
f(x) = x - a, x € [a, a + 1)
şeklinde tanımlanıyor.
2a=13
a=13
/L
Buna göre, f(2) +
11
2
toplamı kaçtır?
B) O
D) 1
2
2-a +
-a
2
15
9
-20 -
0
2
9
19. Bir dikdörtgen altı eş kareye ayrılmış ve bu kareler
monklorinden biri ile boyanacak-

Lise Matematik
Fonksiyon Kavramı ve Gösterimi6) Bir f fonksiyonu, "Her bir pozitif tam sayıyı kendisi ile
çarpımsal tersinin toplamına götürüyor" şeklinde
tanımlanmıştır.
Bu fonksiyon aşağıdakilerden hangisi ile
gösterilebilir?
X
x²+x
A) f(x) =
X-1
B) f(x) =
x²_1
x²_1
X
c) f(x) = x2 + 1
D) f(x) =
X
x²+1
E) f(x) =
X
7) Gercel could
Lise Matematik
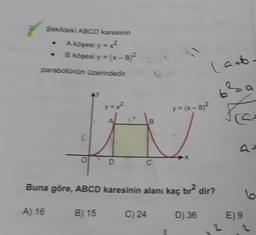
Fonksiyon Kavramı ve GösterimiSekideki ABCD karesinin
A koşesi y=x?
B köşesi y = (x-82
parabolunun üzerindedir.
(ano
}
68
y=x?
y = (x - )2
re
B
c
a
X
D
C
Buna göre, ABCD karesinin alanı kaç br? dir?
6
A) 16
B) 15
C) 24
D) 36
E) 9
2

Lise Matematik
Fonksiyon Kavramı ve GösterimiEgitimde Nelki Saya
5. A = {1, 2, 3, 4} ve B = {-2, -1,0,3,4} olmak üzere
A kümesinden B kümesine bağıntılar tanımlanıyor.
Buna göre, aşağıdaki bağıntılardan hangisi bir fonk-
siyon belirtmez?
A) {(1, -1), (2, 0), (3, 3), (4, -2)}
B) {(4, -2), (3, 0), (2, 4), (1, -1)}
C) {(2, -2), (3, 3), (4, -2), (1, -1)}
D) {(3,-2), (4,0), (3, 4), (2, -2)}
E) {(1, 0), (2,0), (3, 0), (4,0)}

Lise Matematik
Fonksiyon Kavramı ve Gösterimi13. Gerçel sayılarda tanımlı y = f(x) fonksiyonunun grafiği aşa-
ğıda verilmiştir.
y = f(x)
X
- 1
O
3
g, gerçel sayılarda tanımlı doğrusal bir fonksiyon olmak
üzere,
g(x)=3
= 0
f(g(x))
g(x)=-
eşitliğini sağlayan x değerlerinden büyük olan küçük olan-
dan 4 fazladır. MAESTRO
Buna göre, g fonksiyonunun grafiği aşağıdakilerden
hangisi olabilir?
y
A)
YA
B)
2
4
- 1
O
C)
D)
1
X
O
- 1
O
E)
O

Lise Matematik
Fonksiyon Kavramı ve Gösterimiolduğuna göre, a + b kaçtır?
f(x)=(b-6)x+a-2b
g(x)=(a+3)x+c+2
f(30) sabit fonksiyon, g(0) birim fonksiyon olduğuna gö-
re, f(a)+g(b)+c toplamı kaçtır?
(
3-
a=2
f(x) = (a -2) x + 3a + 1
fonksiyonu sabit fonksiyon olduğ
kaçtır?
![5. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
YA
4
1
2
4
X
-2
Buna göre,
f fonksiyonunun değer kümesi R dir.
II. f fonksiyonunun görüntü kümesi (-2, 4] tür.
III. 2f(x) fonksiyonunun tarim kümesi (-8, 4] tür.
ifadelerinden hangileri doğrudur?
A) Yalnız
(B) Yalnız II
C) Yalnız III
gonindy
D) I ve II
E) II ve III](https://media.kunduz.com/media/question/seo/raw/20210315162129464264-275151_ClGeY6jbm.jpg?w=256)
Lise Matematik
Fonksiyon Kavramı ve Gösterimi5. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
YA
4
1
2
4
X
-2
Buna göre,
f fonksiyonunun değer kümesi R dir.
II. f fonksiyonunun görüntü kümesi (-2, 4] tür.
III. 2f(x) fonksiyonunun tarim kümesi (-8, 4] tür.
ifadelerinden hangileri doğrudur?
A) Yalnız
(B) Yalnız II
C) Yalnız III
gonindy
D) I ve II
E) II ve III

Lise Matematik
Fonksiyon Kavramı ve Gösterimi4.
y = f(x) = x2 - 10x
fonksiyonunun grafiği üzerindeki her noktanın y
eksenine göre yansıması alınırsa aşağıdaki fonk-
siyonlardan hangisi elde edilir?
AY - x2 – 10x
B) x2 - 10%
C) -x2 + 10x
D) x2 - X
E) x2 - 5x
be
S
Lise Matematik
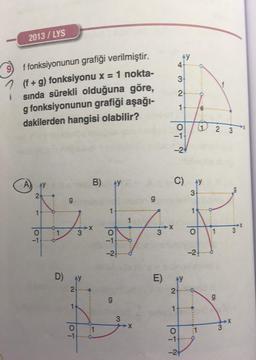
Fonksiyon Kavramı ve Gösterimi2013 / LYS
4
3
f fonksiyonunun grafiği verilmiştir.
1 (f+g) fonksiyonu x = 1 nokta-
sinda sürekli olduğuna göre,
g fonksiyonunun grafiği aşağı-
dakilerden hangisi olabilir?
2
1
o
-1
2
-2
A
B) Y
C) y
3
2
g
1
1
1
1
***
X
X
3
:1
3
-1
-21
-27
D) y
2
E)
y
2
g
9
1
1
3
3
Lol
lor
-2

Lise Matematik
Fonksiyon Kavramı ve Gösterimiharzt3
16+3
9.
f:
RA ve f(x)= x2 - 6x +3
olduğuna göre, f fonksiyonunun örten olması
için A kümesi aşağıdakilerden hangisi olmalıdır?
3-2-5
B) (-6, +00) C) (-3, +00)
| GÜRAY KÜÇÜK YAYINCILIKH
A) R+
D) (-6, +00)
E) (-3, +00)
(x-3) ? 6
