Fonksiyon Kavramı ve Gösterimi Soruları

ÇAP / 10.SINIF 2. DENEME 18. Gerçel sayılarda tanımlıf ve g fonksiyonları için, f+0, g f sabit ve g birim fonksiyon olmak üzere, f(x) · g(x) + f(x) · f(a) = 5-g(x) - a eşitliği veriliyor. Buna göre, f(x) - a işleminin sonucu kaçtır? A) 30 B) 28 C) 25 D) 22 E) 20

4. x f fonksiyonu bire bir ve örten bir fonksiyon olmak üzere, - 2x.f(x) - 1 = 5x + f(x) olduğuna göre, f-'(x) aşağıdakilerden hangi- sidir? A) x + 3 2x-5 X + 1 B) 2x - 3 c) X1 + 2x - 5 ) D) x 5x + 1 2x - 1 5x + 1 E) 2x + 1 E

61. Rakamları birbirinden farklı dört basamaklı xyzt doğal sayı- ları için bir f fonksiyonu f(xyzt) = x.y + 2 +t biçiminde tanımlanıyor. Örnek; f(2304) = 2.3 + 0 + 4 = 10 f(xyzt) = f(zytx) = 17 olduğuna göre, x+y+z+t toplamı kaçtır? -3 A) 14 B) 15 C) 16 D) 17 E) 18 12

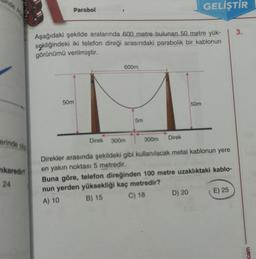
GELİŞTİR Parabol 3. Aşağıdaki şekilde aralarında 600 metre bulunan 50 metre yük- sekliğindeki iki telefon direği arasındaki parabolik bir kablonun görünümü verilmiştir. 600m 50m 50m 5m Direk erinde oly Direk 300m 300m nkaredin 24 Direkler arasında şekildeki gibi kullanılacak metal kablonun yere en yakın noktası 5 metredir. Buna göre, telefon direğinden 100 metre uzaklıktaki kablo- nun yerden yüksekliği kaç metredir? A) 10 B) 15 C) 18 D) 20 E) 25 cam

9. Doğal sayılar kümesi üzerinde tanımlı bir ffonksi- yonu her a ve b doğal sayısı için f(a) f(b) = f(a.b) eşitliğini sağlıyor. f(4)= 9 olduğuna göre, f(2) + f(1) toplamı kaçtır? A) 1 B) 2 C)3 D) 4 E) 5

17. Gerçek sayılar kümesi üzerinde f fonksiyonu f(x) = 2x +8, XS-1 5-X, -1 < x <4 11- 2x x 24 3 biçiminde tanımlanıyor. Buna göre f(a)=0 denklemini sağlayan a değerlerinin toplamı kaçtır? E) 1 11 c) 2 D) 3 2. A) 21 B) 12

Dik koordinat düzlemindel-5, 8) aralığında tanımliffonksiyo- nunun grafiği verilmiştir. y=%) 3 3 2. O Buna göre, 1. (5,8) aralığında i fonksiyonu atandır. II. -4,-2) aralığında i fonksiyonu azalandır. III. f fonksiyonunun 2 tane ekstremum noktası vardır. IV. f fonksiyonunun mutlak minimum değeri -3 tür. V. f fonksiyonunun x = O noktası yerel minimum noktasıdır. ifadelerinden hangileri yanlıştır? A) I ve II B) II ve III C) II, III ve V D) I, IV ve v E) I, II, III, IV ve V

t Test - 3 9. Bir giyim mağazası çalışanları için aşağıdaki gibi bir ücret- lendirme çizelgesi yapıyor. ilk 2 saate kadar ücret 15 TL'dil. İki saatten sonraki her ya- rim saat için 4 Tucret ödenmektedir. Bu şekilde 10 saate kadar çalışılabilmektedir. Giyim mağazası bu ücretlendirmeyi grafiksel olarak ifade etmek istiyor. Bu grafiğe en doğru şekilde karşı- Ik gelen-fonksiyon türü aşağıdakilerden hangisidir? Doğrus A) Sabit fonksiyon B) Doğrusal fonksiyon C) Birim fonksiyon D) Periyodik fonksiyon Parçalı tanımlı fonksiyon

BEST DEGERLEN DI 3. BASAMAK OV 8E854AF9 1. m(t) aylik fatura tutarı (TL) ve t konuşma süresini (dk) göstermek üzere m(t) = 0,2t + 6 fonksiyonu veriliyor. Buna göre, aylık fatura tutarı 22 TL gelen Şenol kaç dakika konuşma yapmıştır? A) 80 B) 75 C) 70 D) 60 E) 56

Test Tee 6. 4. A = {1, 2, 3, 4, 5} f: AA fonksiyonu bire bir fonksiyondur. Her x e A için, g: x "x'in f altındaki görüntüsü ile x sayısının çarpimi" şeklinde tanımlanıyor. g(1) = g(3) = 3 g(5) = g(4) = 20 olduğuna göre, (fog)(2) değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E 7

22. Bir postanede kargo göndermek için alman gün derinin kütlesine (xbağlı alarak belirlenen ücret tarifesi sagidaki fonksiyanla belirtilmiştir. 4 0<x<20 ise f(z) = 7. 20 SX50 ise 10. 50 X 100 ise Buna göre, 36 gramlık ve 72 gramlık iki kar gosu olan kişinin ödeyeceği toplam ücret kay TL'dir? AJ 11 B) 15 C) 16 D) 17 E) 19

Aşağıda 9 odadan oluşan bir oyun kâğıdı verilmiştir. CD YAYINLAR Giriş 2 3 H 5 H 8 7 Çıkış Bu oyun aşağıdaki kurallara göre oynanmaktadır. Oda üzerinde odaların numaraları yazmaktadır. Oyuna giriş kapısından girilip kapılardan geçilerek çıkış kapısından çıkılmaktadır. 8 f(x) = 2x + 3 ve g(x) = 3x – 1 olmak üzere, oyuncu geçtiği her odadan oda numarasının g altındaki görüntüsü kadar puan almaktadır, fakat kullandığı her kapı için oyuncudan (fog)(1) puan düşmektedir. (Giriş ve çıkış kapıları dahil) Her odadan en çok bir kez geçmek koşuluyla bu oyunu oynayan bir oyuncu 5 odadan geçerek en çok kaç puan toplayabilir? A) 40 B) 43 C) 47 D) 51 E) 57 S

23. En yüksek dereceli teriminin katsayısı 1 olan dördüncü dereceden bir polinomun köklerinin birer tam sayı olduğu bilinmektedir. Bu polino- mun grafiğinin, dik koordinat düzleminde eksen- leri kestiği noktalara ait bazı parçaları aşağıda verilmiştir. 72 F T -3 wem Buna göre, bu polinomun katsayıları toplamı kaçtır? A) 72 B) 80 C) 84 D) 92 E) 96 (2019 - AYT) sonuç yayınları

31 da aki Kve 29. Aşağıda şifreli mesaj oluşturmak için her harf 1'den 29'a kadar sayılarla eşleniyor. i A B C ÇDEFG|G|H|I J K L 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 M/NOÖPRSŞTUÜVYZ 16 17 18 19 20 21 22 23 24 25 26 27 28 29 sayı f biçi = = Bir kelime şifrelenirken, kelimedeki her harf f(x) = 3x +1 fonksiyonuna göre aşağıdaki şekilde şifreleniyor. Örneğin, ç harfi alfabede 4. sırada olduğundan f(4) = 3.4 + 1 = 13 bulunur ve ç harfi yerine 13. harf olan J harfi kullanılır. M harfi 16. harf olduğun- dan f(16) = 3 . 16 + 1 = 49 bulunur. Alfabede 49 harf olmadığından, 49 sayısının 29 ile bölümünden kalan bulunur ve M harfi 20. harf olan P harfi ile şifrelenir. = 31 Buna göre, bu yöntem ile "NÇEÇ" kelimesi ile şifrelenen kelime aşağıdakilerden hangisidir? A) NARA B) KARA C) SELE E) LARA D) HALA

lari 5. Aşağıdaki ifadelerden hangileri fonksiyondur? X + 1 I. f: RR, f(x) = x + 3 II. f:N →N, f(x) = 3x+1 III. f: Z → Z, f(x) = X - 4 IV. f: NR, f(x) = x-1 X + 2 A) Yalnız! B) I ve II C) Il ve IV D) I, II ve III E) II, III ve IV

6. 70 yaşındaki Meral Hanım'ın; Erkek çocuklarının sayısı kız çocuklarının sayısı- nin iki katıdır. Her bir erkek çocuğundan 1 torunu, her bir kız ço- cuğundan ise 2 torunu vardır. Çocuklarının yaş ortalaması 40, torunlarının yaş ortalaması ise 22'dir. Meral Hanım'ın kendisi, çocukları ve torunlarının yaş ortalaması 30 olduğuna göre, toplam torun sa- yısı kaçtır? A) 16 B) 12 C) 10 D) 24 E) 20