Fonksiyonlarla İlgili Uygulamalar Soruları
Lise Matematik
Fonksiyonlarla İlgili Uygulamalar-triği
2
E) -7
daki-
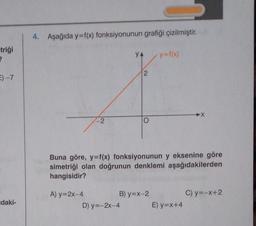
4. Aşağıda y=f(x) fonksiyonunun grafiği çizilmiştir.
-2
YA
2
D) y=-2x-4
B) y=x-2
y=f(x)
Buna göre, y=f(x) fonksiyonunun y eksenine göre
simetriği olan doğrunun denklemi aşağıdakilerden
hangisidir?
A) y=2x-4
▶X
E) y=x+4
C) y=-x+2

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar2. Aşağıda y=f(x) fonksiyonunun grafiği çizilmiştir.
A)
C)
21
O2
Buna göre, y=f(-x) fonksiyonunun grafiği aşağıdaki-
lerden hangisidir?
AY
-2
2
2
E)
AY
▶X
2
-2
2
y=f(x)
O
X
B)
02
-2
D)-AY
2
AY
2
02 4
eis
Toyinion
5.

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar13. Gerçel sayılar kümesinde tanımlı bir f fonksiyonunun gra-
fiği y eksenine göre simetriktir.
p bir gerçel sayı ve f(x + p) = x² - 6x +11
olduğuna göre,
1. p = -3
II. f(p) = 11
III. f(x) in en küçük değeri -3 tür.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
576
D) I ve II
E) I ve III
C) Yalnız III
15. m

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar7.
-2
A) 6
A
B) 9
O
B
4
y = f(x) parabolünün grafiği verilmiştir.
Parabolün tepe noktasının ordinatı y = -3 doğrusu üzerinde-
C) 12
y = f(x)
dir.
Buna göre, köşeleri A, B ve parabolün tepe noktası olan
üçgenin alanı kaç br² dir?
➤X
D) 15
E) 18

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar29. Gerçel sayılar kümesi üzerinde tanımlı bire bir ve örten f ve
g fonksiyonları için
f(g(x)));
X+2
(fog)(x) = -x + 2
(gof)(x) = x <a
(fof)(3) = 14
f
Buna göre, (fof)(-8) değeri
A) 6
B) 8
f(x)
MORE
f(f(-8)) = ?
C) 25 D) 26
(+
(4 (3)) = 14
kaçtır?
f(3) = X
f(x) = 19
Buna göre, m
be cetvel üzer
gelir?
A) 5
E) 27
f(x) = 14
(3)=x
B)

Lise Matematik
Fonksiyonlarla İlgili UygulamalarSARIŞIR
CARPANLARA AVIRMA
1
Yukandaki şekilde O merkezli r, ve r, yarıçaplı iki da-
ire veriliyor.
Dairelerin arasında sıralanmış taralı bölgenin alanı
20 cm ve dairelerin çevrelerinin toplamı 20x cm
olduğuna göre bu dairelerin yarıçapları farkı r₁-1₂
nedir?
A) 2 B) 3
D) 5 E) 6
C) 4

Lise Matematik
Fonksiyonlarla İlgili UygulamalarBİRLİKTE YAPALIM
A={1, 2, 3, 4) ve B = {4, 5, 6, 7) kümeleri veriliyor.
A kümesinden B kümesine kaç farklı fonksiyon tanım-
lanabilir?
A kümesinden B kümesine kaç farklı bire bir olmayan
fonksiyon tanımlanabilir?
Lise Matematik
Fonksiyonlarla İlgili Uygulamalar6
a-3
E6
nun
tır?
72
5
✔FEN BİLİMLERİ YAYINLARI
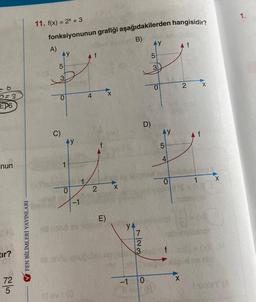
11. f(x) = 2x + 3
fonksiyonunun grafiği aşağıdakilerden hangisidir?
B)
A)
5
3
0
C)
AY
0
id mand
-1
4
f
2
E)
X
YA
723
D)
-10
AY
5
3
TO
AY
4
0
f
X
2
f
A f
1
X
X

Lise Matematik
Fonksiyonlarla İlgili Uygulamalarf fonksiyou [0, ∞0) aralığında tanımlı artan bir fonksi-
yondur.
f fonksiyonunun grafiğinin orijine göre simetrisi çizildi-
ğinde g fonksiyonun grafiği elde edilmektedir.
f(2)=4
g(-5) = -8
olduğuna göre,
f(3) + g(-4)= a
eşitliğini sağlayan a sayısının alabileceği değerlerin
en geniş aralığı aşağıdakilerden hangisidir?
A) (-4, 8)
B) (0, 1)
(-4,0) 1 E) (-4,4)
C) (-1, 1)
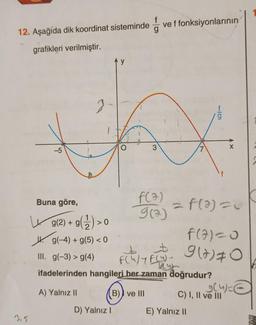
Lise Matematik
Fonksiyonlarla İlgili Uygulamalar12. Aşağıda dik koordinat sisteminde
grafikleri verilmiştir.
3,5
-5
Buna göre,
g(2) + g(¹1) >
g(2) +
g(-4) + g(5) < 0
>0
O
D) Yalnız I
3
(B) ve III
ve f fonksiyonlarının
f(*)
9(2)
7
III. g(-3) > g(4)
F(W/YF(W)
ifadelerinden hangileri her zaman doğrudur?
A) Yalnız II
g
= f(a)=0
X
f(7) = 0
9(+) #0
E) Yalnız II
(4)=(
C) I, II ve III

Lise Matematik
Fonksiyonlarla İlgili UygulamalarTEST-11
f(x) = ax+b
Bir f(x) fonksiyonunun periyodu 3 olduğuna göre,
g(x) = f(5x + 1) +3
fonksiyonunun periyodu kaçtır?
3|6
A) -
f(x+ 7) = f(x)
2|5
B) -/-/-
2
c) -/-/-
C)
3
D) 2
tekijk
XT = 201
lal
101
E) 3
4.

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar2022-AYT/ Matematik
37. Kalkış noktası orijin olarak kabul edilen uçak önce y = 2x
doğrultusunda yükselişe geçip yerden 4 br yükseklikteki
A noktasına geldikten sonra yere paralel uçuşa geçiyor.
A
A) 2x -y + 14 = 0
C) 2y-x+6=0
B
4 br daha ilerledikten sonra, orijinden 14 br uzaklıktaki C
noktasına varmak için B noktasında inişe geçiyor.
Yukarıdaki verilere göre, uçak hangi doğru boyunca
inişe geçmiştir?
X
E) 2y + x - 14 = 0
B) 2x + y - 14 = 0
D) 2x - 3y + 12 = 0
LİMLERİ YAYINLARI
3

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar2022-AYT / Matematik
25. y = f(x) fonksiyonunun grafiği orijine simetriktir.
f(-x) + x³ = 2f(x) + x
olduğuna göre, f(2) değeri kaçtır?
A) 1
B) 2
A
C) 3
y
D) 4
E) 5
26. Aşağıdaki şekilde y = |x| fonksiyonunun grafiği verilmiştir.

Lise Matematik
Fonksiyonlarla İlgili UygulamalarFONKSİYONLARDA ÖTELEME TEK ÇİFT
Analitik düzlemde verilen y = f(x) fonksiyonunun grafiği,
4 birim sağa,
• 2 birim yukarı
●
ötelendiğinde aşağıdaki eğrilerden hangisi elde edilir?
A) y = f(x + 2) + 4
B) y = f(x-2) + 4
C) y = f(x-4)-2
D) y = f(x-4) + 2
E) y = f(x + 4) + 2
y = f(x) eğrisi üzerinde alınan A(-1, 3) noktasının
20.

Lise Matematik
Fonksiyonlarla İlgili Uygulamalarf(x) = x² - 4x + 5
fonksiyonu x ekseninin pozitif yönünde 3 birim öte-
lendikten sonra, y ekseninin negatif yönünde 4 bi-
rim ötelenerek y = g(x) fonksiyonu elde ediliyor.
Buna göre g(2) kaçtır?
A) 4
B) 5
36
G
D) 7
E) 8
10.

Lise Matematik
Fonksiyonlarla İlgili Uygulamalar12. Ayrıt uzunlukları a, b, c olan dikdörtgenler prizmasının hacmi
a b c'dir.
.
Bir ayrıt uzunluğu 2 cm olan küpler ile oluşturulan bir örün-
tünün ilk üç adımı aşağıda verilmiştir.
1. Adım
2. Adım
A) 100
Buna göre, örüntünün 5. adımındaki cismin hacmi kaç
cm³ tür?
B) 144
3. Adım
C) 150
D) 200
