Fonksiyonlarla İlgili Uygulamalar Soruları

4D Serisi Ⓡ 8. Aşağıda y = f(x) ve y = g(x) fonksiyonlarının grafikle- ri verilmiştir. y = f(x) A) Yalnız I 4 Buna göre, 1. y = |g(x) | ile y = f(x) + 2 fonksiyonlarının grafik- leri 3 farklı noktada kesişir. D) II ve III X II. y = -f(x) ile y = g(x) - 2 fonksiyonlarının grafikle- ri 3 farklı noktada kesişir. y = g(x) III. y = g(x) ile y = f(x) | fonksiyonlarının grafikleri 3 farklı noktada kesişir. ifadelerinden hangileri doğrudur? B) Yalnız III E) I, II ve III C) I ve II

A $ A R 1 1 1 1 R R R 1 1 4 1 1 1 $ R # R 1 $ 1 * A A T 9 3 2 0 -2 2 5 X Grafiği verilen f(x) fonksiyonunun; a) Eksenleri kestiği noktaları bulunuz. b) Pozitif ve negatif değer aldığı aralıkları bulunuz. c) Artan ve azalan olduğu aralıkları bulunuz. d) Maksimum değeri kaçtır? e) Minimum değeri kaçtır?

5. (a + 3). (a-1) = 0 a= -3,1 f(x) = A) E X-1 x² - ax +4 = 0 LACO fonksiyonu her x gerçek sayısı için tanımlı olduğuna göre, a'nın alabileceği kaç farklı tam sayı değeri var- dır? B) 6- (C) 7 D=b² hac α-4.1.460 Dre E9 Her x gercek Soyisi ian toom ise 4

eser. X eksenini 1-4.1.16 1-64 +X+ 16 20 -b 29 2-4+5 -7 12. f(x) = 2x² + 4x +5 -4 4 B) -6 2 C) -3 -1 3. D) 1 E) 6 11. SINIF MATEMATİK SB/C SERİSİ parabolünün tepe noktası T(r, k) olduğuna göre r.k çarpımı kaçtır? A) -10 f: R ek

Dik koordinat düzleminde y = f(x) fonksiyonuna aşa- ğıdaki işlemler uygulanıyor. Fonksiyonun grafiği çiziliyor. ● ● ● ● Çizilen grafiğin x eksenine göre simetrisi alınıyor. Elde edilen fonksiyonun grafiği yatay eksende 3 bi- rim sağa öteleniyor. Bu işlemler sonunda elde edilen fonksiyon g(x) fonksiyonu oluyor. Buna göre, g(x) fonksiyonu aşağıdakilerden han- gisidir? A) g(x) = -f(x + 3) C) g(x) = f(-x-3) B) g(x) = f(-x) + 3 g(x) = -f(x-3) E) g(x) = -f(x) + 3

E) 5 4. f: R-(2)→R - (0) olmak üzere y = f(x) fonksiyonu x³y-6x²y + 12xy-8y-4 = 0 şeklinde tanımlanıyor. Buna göre, f¹(x) in kuralı aşağıdakilerden hangisidir? 9√4+2 A) 4 + 2x X D) ³√4-2 x²(xy-by) - 4y ( 3x - 2)-4 = 0 √4+2 4 BİR FC ÖZELL f: R-RE 1: R-RE for¹ = ¹, f: R-R, f(. olduğuna NEU

2. f(x) = 3x + 4x² - 13 fonksiyonu için; 1. fonksiyonun grafiği y eksenine göre simetriktir. II. fonksiyonun grafiği x eksenine göre simetriktir. III. fonksiyonun grafiği orijine göre simetriktir. IV. fonksiyonun grafiği y = x doğrusuna göre simet- riktir. V. f(-x) = f(x) tir. ifadelerinden kaç tanesi doğrudur? A) 1 B) 2 C) 3 D) 4 E) 5

C) 6 D) 8 E) 10 mimli f ve g fonksi- 2 - g)(x) fonksiyonu- kilerden hangisi- B) x² - 2x + 1 D) x² + 6x + 6 +2 9. f: RR tanımlı f(x) fonksiyonu için f(2x - 5) = 4x-3 olduğuna göre, f¹(4x + 3) fonksiyonu aşağıdakilerden hangisidir? B) 2x - 7 D) 2x - 2 X-7 A) 2 C) 4x - 3 E) 2x + 7 12. Re fw ol A

1) fonksiyonu- aşağıdakiler- f(x) + 4 f² (x) 8 13. f(x) = 4x - 2 g(x) = 3x + 1 fonksiyonları için (fog)(a) = 26 oldu- ğuna göre, a değeri kaçtır? A) -1 B) 1 C) 2 D) 3 E) 5 118 Grafic 1. Ta 11. G ifad A)

B A 23 A 1. 2. 3- B -a -C -d B a -C å 4. f(x) fonksiyonu çift fonksiyondur. f(3) = 7 f(-3) = 2a +3 olduğuna göre, a değeri kaçtır? A) -7 B)-5 C) -2 D) 2 E) 5 5. f: R-(2)→ R-(-2) olmak üzere, f fonk- 8. Uygun aralı fonksiyonu ni sağlama Buna göre kilerden b A) f-1(x) B) f(x C) f(x

-X g(x) n grafikleri veril- 6. y=f(x) fonksiyonu (-1, 3) aralığında artandır. Buna göre, > arrande f(x) - 1 fonksiyonu (0, 4) aralığında artandır. O 1. II. y = -f(x) fonksiyonu (-1, 3) aralığında azalandır. Ill. y = f(x-2) fonksiyonu (1, 3) aralığında artandır. ifadelerinden hangiler kesinlikle doğrudur? A) Yalnız I B) Yalnız II D) I ve II C) Yalnız III E) II ve III (x)=x 9. y=f(x) y Buna göre, y=f(x)=1 11. y=-x fix-2) fonksiyonlar artandir? A) Yalnız I

1. 16 kişilik bir sınıfta Fransızca bilenler kümesi F, Almanca bilenler kümesi A dir. s(F) = 8, s(A) = 9. s(AF) = 14 olduğuna göre, bu sınıfta sadece Almanca bilen kaç kişidir? C) 5 D) 6 A) 3 B) 4 E) 7 F A (1981/11) 2

4D Serisi Ⓡ 11. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir. A) f(x) Buna göre, f(x) fonksiyonunun x eksenine göre, si- metriği aşağıdakilerden hangisidir? C) 4 YA 3 2 O 3 2 YA 3 B) 4 D) 44 X X 11. Sınıf-MATEMATİK

8. BİLGİ: f(-x) = -f(x) şartını sağlayan fonksiyonlara tek fonksiyon denir. Tek fonksiyonların grafikleri orijine gö- re simetriktir. Buna göre, aşağıda verilen fonksiyonlardan hangi- sinin grafiği orijine göre, simetrik değildir? A) f(x) = sinx B) f(x) = tanx D) f(x) = 2x5 - 4x C) f(x) = x³ (E) f(x) = 3x - 5 E) ₁

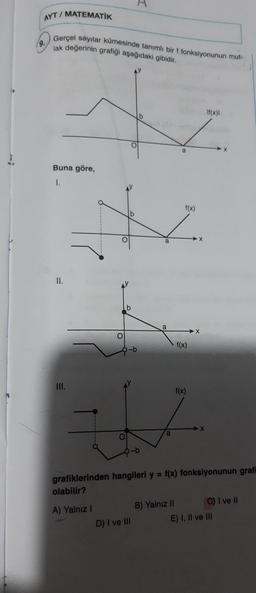
9. AYT / MATEMATİK Gerçel sayılar kümesinde tanımlı bir f fonksiyonunun mut- lak değerinin grafiği aşağıdaki gibidir. Buna göre, I. III. O A) Yalnız I a D) I ve III a a a B) Yalnız II f(x) f(x) f(x) X X grafiklerinden hangileri y = f(x) fonksiyonunun grafi olabilir? ➜X If(x)\ C) I ve Il E) I, II ve III

Ornek-3 f = {(-7, 4), (6, 2), (3, 3), (1,5)} g= {(6, 3), (3, 2), (2, 5), (-7, 1)} fonksiyonları veriliyor. 3f- 2g fonksiyonunun görüntü kümesindeki ele- manların toplamını bulunuz. çözüm-3 Ör Ge eş mi B