Fonksiyonlarla İlgili Uygulamalar Soruları

10. 5a7b sayısı ile ilgili, ● ● degies Rakamları farklı dört basamaklı bir sayıdır. Sayıya 7 eklendiğinde 15 ile tam olarak bölün- mektedir. bilgileri verilmiştir. NOW Buna göre, 5a7b sayısında a'nın alabileceği değer- ler toplamı kaçtır? A) 12 B) 13 C) 15 D) 28 E) 33

10. -6 5 Yukanda f(x) fonksiyonunun grafiği verilmiştir. (-6,10] ara- lığında, A. 9 10 f(x) = -f(x) eşitliğini sağlayan x tam sayı değerleri- nin toplamı A, B) 5 f(x) = f(x) eşitliğini sağlayan x tam sayı değerlerinin toplamı B, olmak üzere, A - B farkı aşağıdakilerden hangisidir? A) 7 C) 3 D) 2 E) 1

Test 1 20. Tanım kümesi iki basamaklı doğal sayılardan oluşan f ve g fonksiyonlan, f(AB) = (A + 1). (B-1) g(AB) = A + B-1 biçiminde veriliyor. Buna göre, 3x ve x6 iki basamaklı doğal sayıları için, FONKSİYONLAR f(3x) = g(x6) eşitliği sağlandığına göre, xx iki basamaklı sayısı için f(g(xx). f(xx)) işleminin sonucu kaçtır? B)-5 A) 5 C) 7 D) -3 E) 6

20. Tanım kümesi iki basamaklı doğal sayılardan oluşan f ve g fonksiyonları, f(AB) = (A + 1). (B-1) g(AB) = A + B-1 biçiminde veriliyor. Buna göre, 3x ve x6 iki basamaklı doğal sayıları için, f(3x) = g(x6) eşitliği sağlandığına göre, xx iki basamaklı sayısı için A) 5 f(g(xx). f(xx)) işleminin sonucu kaçtır? B)-5 C) 7 D) -3 E) 6

18. (=v f(x)=x²-√33x+m-20 fonksiyonunun grafiğine göre, x eksenini kestiği noktalardan çizilen teğetler birbirlerine dik olduğuna göre, m kaçtır? A) 6 B) 7 03 Deneme Sınavı - 05 in 6=√33 a+b= a.b= C) 8 D) 9 Trips hapub (S)(gol) E) 10 BADO & (8 S (A

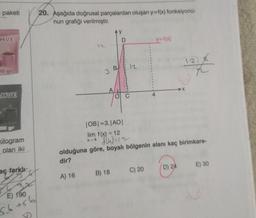
paketi HVE 00 gr HVE 00 gr kilogram olan iki aç farklı G E) 190 5.6 +56/ 20. Aşağıda doğrusal parçalardan oluşan y=f(x) fonksiyonu- nun grafiği verilmiştir. n A) 16 Ay B) 18 B D 12 C y=f(x) |OB| =3. |AO| lim f(x) = 12 x-4 J(u) = 12 olduğuna göre, boyalı bölgenin alanı kaç birimkare- dir? C) 20 4 24 D) 24 E) 30

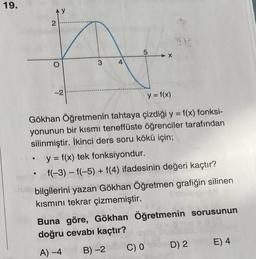
7. - 1 > 5 3 O 2 IN X C) - 1 y = f(x) Şekilde y = f(x) fonksiyonunun grafiği verilmiştir. g(x + 2) + f(x - 2) = x + 1 olduğuna göre, g(3) kaçtır? A) - 5 B) - 3 D) 1 E) 3 1 AC 2 AC A C 4 (A) 5 (A 6 7 8 10

19. 2 ● -2 3 4 LO 5 y = f(x) Gökhan Öğretmenin tahtaya çizdiği y = f(x) fonksi- yonunun bir kısmı teneffüste öğrenciler tarafından silinmiştir. İkinci ders soru kökü için; y = f(x) tek fonksiyondur. f(-3) -f(-5) + f(4) ifadesinin değeri kaçtır? bilgilerini yazan Gökhan Öğretmen grafiğin silinen kısmını tekrar çizmemiştir. Buna göre, Gökhan Öğretmenin sorusunun doğru cevabı kaçtır? A) -4 B) -2 C) 0 D) 2 E) 4

TYT/ Temel Matematik 24. Uygun tanım aralığında, bir fonksiyon aşağıdaki gibi ta- nımlanıyor. f^(x) = x + (n pozitif bir tam sayı) f¹(x) = 1 olduğuna göre, f20 (x) değeri kaçtır? A) 40 B) 20 C) 0 D) -1 20 x t (+4) 20 1 20 x 20 1 20 t GO 20 x' + 20 20 20 x 10+ 20 1 Q₁ x + 1 = 1 x 20 +0 E)-20 P(x), Q(x) ve R(x) ikinci dereceden başkatsayıları sıra- sıyla 1,-1 ve 2 olan polinomlardır. 26. Asli, Berer bilgisayard 11 20 Bu alışveri • p: "Asl q: "Ber r: "Car önermeler 0. (pv q) Buna gör rasıyla a Te As Tele Tele 7 A) SODE Tab DY Tal E) Bilgis

AYT 7. Dik koordinat düzleminde [0, 4] aralığında tanımlı bir f fonksiyonunun grafiği aşağıda verilmiştir. 2 y = f(x) Buna göre, 1. (fof)(x) = 2 eşitliğini sağlayan dört farklı x değeri var- dır. D) II ve III II. (fof)(x) = 0 eşitliğini sağlayan iki farklı x değeri var- dır. III. (fof)(x) = 4 eşitliğini sağlayan farklı x değerlerinin toplamı 6 dır. ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II C) I ve II 1, II ve III:

? D) 7 E) 9 Paraf Yayınları 4220 ažçb² 2124 923-04 53. Gerçel sayılarda tanımlı bir f fonksiyonu her x gerçel sayısı için f(x + 3) = x f(x + 1) A) 7! (2x-122x eşitliği ile veriliyor. f(3) = 2 olduğuna göre, f(17) kaçtır? f(s) ₂ B) 27.7! D) 14! 29 22. E) 14! C) 28.71 A A) 84 2. K L 8 |DE| = |EF| = |FG| = |GH| = AB=30 cm ve |KE| = |MG| Buna göre, geriye kalan kısmı B) 90 30 M C) Bir tel şekildeki gibi kıvrıl

58. y=mx ² (m ² 1 B O Yukarıdaki şekilde 2y = nx + 12 doğrusu ile tepe noktası y ekseni üzerinde olan A) 36 y=mx² - (m²-1)x-3m-1 parabolünün grafiği verilmiştir. 2y=1x+12 Doğru ile parabol A ve B noktalarında kesişmiştir. Parabolün x eksenini kestiği noktalar B ve C dir. J Buna göre, ABC üçgeninin alanı kaç br² dir? B) 42 C) 48 D) 64 E) 72 60

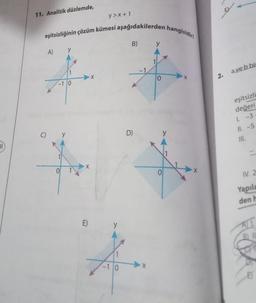
11 11. Analitik düzlemde, eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir? A) () y -1/0 0 ****** X E) y>x+1 X 1 -10 B) D) -1 y 0 y 0 -X X 2. a ve b bi eşitsizli değeri 1. -3 11. -5 III. IV. 2 Yapıla den h ALL. B) II E)

TEST -1- €3 9. f: R→ Rolmak üzere, A) f(x) + 7 FONKSİYON f(x + 4) = 2x + 5 fonksiyonu veriliyor. Buna göre, f(3x + 1)'in f(x) türünde eşiti aşağıdakilerden hangisidir? A) 5 that Xxx=-4 D) f(x) - 8 B) 3f(x) + 8 x +4=3x + 1 3=24 • g(x + 1) = g(x) + 4 f(x) + g(x) = x² + 2x-3 2 B) 6 10. Tam sayılar kümesi üzerinde tanımlı f ve g fonksiyonları, her x tam sayısı için C) 8f(x) + 3 E) 2f(x) - 15 eşitlikleri sağlıyor. g(4) = 10 olduğuna göre, f(2) değeri kaçtır? C) 7 1984 PASAR D) 8 13. f doğ f(2x) E) 9 A) 5 14. f

isi ek- Til- 2 6 karekök 323 D ● Ikiz kenarlarından birinin uzunluğu, taban kenarının uzunluğundan 3 birim fazla olan ABC ikizkenar üçgen- lerinin çevresini veren f(x) ve g(x) fonksiyonlarını Aslı ile Bensu şöyle yazıyorlar. 2 x+3 7 Aslı, ABC üçgeninin ikiz kenarlarından birinin uzun- luğunu x birim alıyor. A B B Buna göre, A O C Bensu, ABC üçgeninin tabanının uzunluğunu x birim alıyor. X C) 27 8 D) 24 C A f(x) - g(x) işleminin sonucu aşağıdakilerden hangisidir? A) 6x + 9 B) 9 C) 6x D) -9 f(x) = Çevre (ABC) 9 g(x) = Çevre (ABC) E) 16 A 10 E E) -12 11 D

ÖRNEK 32 E Aşağıda 3. dereceden denklemler ve bu denklemlerin karmaşık sayılardaki çözüm kümeleri ile ilgili bilgiler verilmiştir. 2002200 1. (x-1)³ = 0 çözüm kümesi tek elemanlıdır. II. x³ = 8 iki sanal bir gerçel kökü vardır. III. x³ + x² - x - 1 = 0 çözüm kümesi iki gerçel kökten oluşur. IV. x²(x+2) = x+2 üç farklı gerçel kökü vardır. Buna göre, bu ifadelerden kaç tanesi doğrudur? A) O B) 1 C) 2 D) 3 E) 4