Fonksiyonun Grafiği Soruları

Lise Matematik
Fonksiyonun GrafiğiFONKSİYONLAR
10. 1-1 ve örten f ve g fonksiyonları için,
fog(3x+2) = f(5x-10)
11.
such
olduğuna göre, g ¹(10)+g(23) toplaminin değe-
ri kaçtır?
A) 33 B) 35 C) 36 D) 37 E) 39
f(g(3x+2)) = (5x-10)
2-13
f(x) = x - 13/
12 41
2v-17
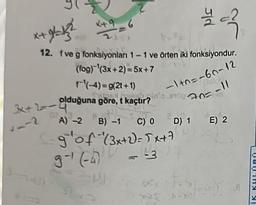
Lise Matematik
Fonksiyonun GrafiğiX49 6
4+b√²
12. f ve g fonksiyonları 1-1 ve örten iki fonksiyondur.
(fog)(3x+2) = 5x+7
X
Jjd
(-4)=g(2t+1)
olduğuna göre, t kaçtır?inta en
3x+2-Olduğuna göre, t kaçtır?
(10%)
-1+0=-60-12
ARE I
8
A) -2 B) -1 C) 0
glof (3x+2) = 5x+7
9-¹ (-4)
-3
D) 1 E) 2
-
IK KULÜBÜ

Lise Matematik
Fonksiyonun GrafiğiO
10. f ve g fonksiyonları için,
f(3x-5) =
fog (2x+1)=2x² - 5x+3
X-1
g(x+1)=3x-5
3 (x-1)-5
olduğuna göre, f(7)'nin değeri kaçtır? 3-8
D) 4
E) 5
291
C) 3
A) 1
B) 2
g(x) = 3x-8
3(2x+1)-8
3x+3-8
Matematik Kulübü

Lise Matematik
Fonksiyonun Grafiğiheim Konu Pekiştirme - 3 MY20
mo
5. Uygun şartlar altında,
Zygun
1(x-2) X+1
bisliysa Negis
X+1
2-x
olduğuna göre, f(x) fonksiyonu aşağıdakilerden
hangisidir?
A) X
D)
-
1
x+1
B)
-
1
×|-
X
E) X - 2
Sh blo
C) x + 1
gious
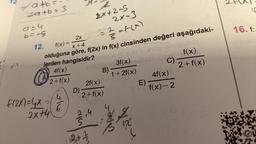
Lise Matematik
Fonksiyonun GrafiğiX!(
✓a+b=-
2a+b = 3
a=4
b=-5
12.
2x-3
2x
f(x) =
= ²/3 = f(x)
x+4
nebylerden
4f(x)
S
olduğuna göre, f(2x) in f(x) cinsinden değeri aşağıdaki-
hangisidir?exnot (8 + x) 1,öp nupuble
Shible 3f(x) elbisbiosi f(x)
2+ f(x)
B)
C)
1+2f(x)
2+ f(x)
f(2x) = 4x =
2x+4
4
6
D)
2f(x)
2+ f(x)
2.4
dis
2
2x+2-S
2 + 2/20
Ape
4f(x)
f(x) - 2
E) -
harde
16
16. f:
leon
Lise Matematik
Fonksiyonun Grafiğiçi
3
4D Serisi Ⓡ
Çözüm:
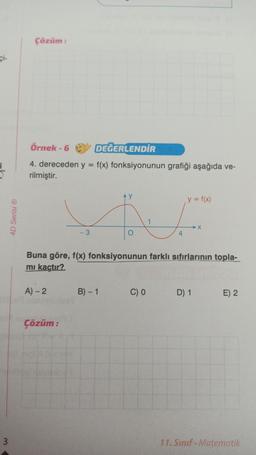
Örnek-6
DEĞERLENDİR
4. dereceden y = f(x) fonksiyonunun grafiği aşağıda ve-
rilmiştir.
A)-2
- 3
Çözüm:
4
Buna göre, f(x) fonksiyonunun farklı sıfırlarının topla-
mı kaçtır?.
B) - 1
y = f(x)
X
C) 0 D) 1
E) 2
11. Sınıf Matematik

Lise Matematik
Fonksiyonun Grafiği6
5.
f ve g doğrusal fonksiyonlar olmak üzere,
(fog)(x) = 3-g(x) + 2
eşitliği veriliyor.
f fonksiyonunun grafiği, x ekseninin pozitif yönün-
de 2 birim ötelendikten sonra y ekseninin negatif yö-
nünde de 2 birim ötelenmesiyle g fonksiyonunun gra-
fiği elde edildiğine göre, g(2) kaçtır?
B) 1
C) 2
A) O
D) 3
E) 4

Lise Matematik
Fonksiyonun Grafiği12. A (-2,-1, 1, 2) olmak üzere,
f(x) =
yapboz parçaları birleştirilerek A kümesinde tanımlı
f fonksiyonu
f(x) =
A)
x² + 1
ve
elde edilecektir.
Buna göre, bu yapbozun mavi parçası aşağıda-
kilerden hangisi olursa elde edilen fonksiyonun
görüntü kümesi {2, 5} olur?
B)
D)
X +3
= 7B 8B 9B 10C11C12A|
x² + x
X +3
X + 1
E)
C)
x²-1

Lise Matematik
Fonksiyonun Grafiğix₁ ve
özüm
<2
Do
+
++
13.
-3
f(x)
Buna göre,
X-2
larının toplamı kaçtır?
A) 30
B) 29
O
mul musco
Yukarıdaki şekilde f(x) fonksiyonunun grafiği verilmiştir.
100
%
C) 26
< 0 eşitsizliğini sağlayan x tam sayı-
X+2
D) 25
E) 21

Lise Matematik
Fonksiyonun Grafiği8.
BH
-ab +12
a ve b birer gerçek sayı olmak üzere,
f: R - {b} → R
ax + 12
x-b
f(x) =
2
6x +12 ? Sabit
3
xta
3 fonksiyonu tanımlanıyor.
b =
f fonksiyonu bire bir olduğuna göre,
aşağıdakilerden hangisi kesinlikle yanlıştır?
A) a+b = 12
C) a∙b=12
E)ab 6
lo
(2)
12
ab=12
B2b = -12
Drab=12

Lise Matematik
Fonksiyonun Grafiği8. Bir öğrenci aşağıdaki iddiayı ispatlamaya çalışmak-
tadır.
İddia:
Öğrencinin ispatı:
Her ye Y için
1. En az bir xEX için f(x) = y
9₁(y) = 9₁(f(x)) = (g₁of)(x)
(g₁of)(x) = (9₂0f)(x)
(92of)(x) = 92(f(x)) = 9₂(y)
Her yeY için g₁(y) = 92(y)
II.
III.
IV.
V.
f: X→Y ve 91, 92: Y → Z
g₁of=g2of ise 9₁ = 92 dir.
olduğuna göre, g₁ = 92 olur.
Bu öğrenci numaralanmış adımların hangisinde
hata yapmıştır?
A) I
B) II
Q
D) IV
E) V

Lise Matematik
Fonksiyonun GrafiğiERECEDEN İKİ BİLİNMEYENLİ DENKLEMLER
4
y = x² - 6x² + 1
y = x
denklem sisteminin kaç farklı özel kökü vardır?
an
4.
A) O
B) 1
x= x² - 6x²1
=x4-6x²-**1
x2(x²_6) -x+1
C) 2
52
D) 3
E) 4
BÖLÜM
1
€
aittir.
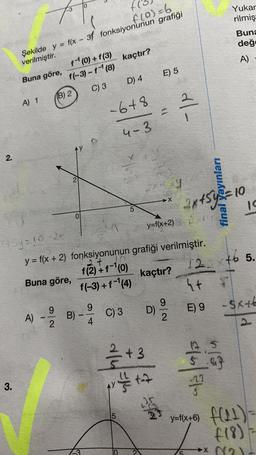
Lise Matematik
Fonksiyonun Grafiği2.
f
f(0) = 6
Şekilde y = f(x - 3 fonksiyonunun grafiği
verilmiştir.
3.
Buna göre,
A) 1
4 Sy=10-2x
(B) 2
A)
f-¹ (0) + f(3)
f(-3) -f-¹ (8)
C) 3
9
2
y = f(x + 2) fonksiyonunun
2+
f(2) + f-¹(0)
Buna göre,
f(-3)+f-¹(4)
B)
9
4
kaçtır?
-6+8
4-3
D) 4
C) 3
5
E) 5
D)
+3
X
2
pxry
y=f(x+2) xf
92
9
grafiği verilmiştir.
kaçtır?
2x+5y8=10
final Yayınları
5
122x+6
ht
E) 9
12 5
47
y=f(x+6)
Yukar
rilmiş
Buna
değe
A)
:47
19
+6 5.
-5x+b
f(11)-
((8)
** N₂1-

Lise Matematik
Fonksiyonun Grafiği3
9. m ve n sıfırdan farklı gerçel sayılar olmak üzere, gerçel sayı-
lar kümesinde tanımlı bir f fonksiyonu,
f(mx + n) = m + nx
f(2m) = m + n
eşitliklerini sağlıyor.
Buna göre,
2f (m) + f(n)
f(2m) - f(n)
ifadesinin değeri kaçtır?
A)
112
B) 1
C)
c) 3/20
MXLA
40
D) 2
E) 3
Diğer sayfaya geçiniz.

Lise Matematik
Fonksiyonun Grafiği9. Ticari taksiye binen bir kişinin, alınan yola (km) göre
ödeyeceği ücret
x
2x
fonksiyonu ile belirlendiğine göre, bu kişinin Hk-10
km'de ödeyeceği ücretin değişim hızı kaçtır?
A) 2,8
B) 4,6
C) 5,2
D) 5
1-B
f(x) =
=
2
2-E
2
+4
3-E
4-D
5-C
6-C
E) 6
7-C
![●
9.
n bir pozitif tam sayı, f(x) fonksiyon olmak üzere f(x) değeri,
n sayısı tek ise f(x) = n · [f(x)]+1
.
n sayısı çift ise f(x) = n.
[f(x)]-1
olarak tanımlanıyor.
Buna göre,
f(x) = x² + x
g(x) =
1
X-1
2 +01
p₁
fonksiyonu için,
D) [-1, 2]
P
12(x) g³(x) ≤0
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
A) [-1, 0]
B) [-1, 1]
C) [0, 1]
E) [0, 2]](https://media.kunduz.com/media/question/seo/raw/20230206195031188920-4836135.jpeg?w=256)
Lise Matematik
Fonksiyonun Grafiği●
9.
n bir pozitif tam sayı, f(x) fonksiyon olmak üzere f(x) değeri,
n sayısı tek ise f(x) = n · [f(x)]+1
.
n sayısı çift ise f(x) = n.
[f(x)]-1
olarak tanımlanıyor.
Buna göre,
f(x) = x² + x
g(x) =
1
X-1
2 +01
p₁
fonksiyonu için,
D) [-1, 2]
P
12(x) g³(x) ≤0
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
A) [-1, 0]
B) [-1, 1]
C) [0, 1]
E) [0, 2]
