Fonksiyonun Grafiği Soruları
![8
ÖRNEK - 9
Aşağıdaki şekilde y = f(x) fonksiyonunun grafiği ve-
rilmiştir.
2
1
4
Af
-3 0
-2
-3
-5
y = f(x)
v
67
X
Buna göre, bu fonksiyonun,
1. Tanım kümesi [-5, 6]'dır. V
II. Görüntü kümesi [-3, 2]'dir.
III. Görüntü kümesinin en büyük değeri 2 dir.
IV. Görüntü kümesinin en küçük elemanı -3'tür.
V. Üç tane sıfırı vardır.
ifadelerinden hangileri doğrudur?
yarıçap
M
TANIM
Nümesp
Aşağı
grafiğ
xelisen
SA
Garint
Home
ne
f(x)'in
ve b.
Bun
Cisco
E](https://media.kunduz.com/media/question/seo/raw/20230206194925109050-4690891.jpg?w=256)
Lise Matematik
Fonksiyonun Grafiği8
ÖRNEK - 9
Aşağıdaki şekilde y = f(x) fonksiyonunun grafiği ve-
rilmiştir.
2
1
4
Af
-3 0
-2
-3
-5
y = f(x)
v
67
X
Buna göre, bu fonksiyonun,
1. Tanım kümesi [-5, 6]'dır. V
II. Görüntü kümesi [-3, 2]'dir.
III. Görüntü kümesinin en büyük değeri 2 dir.
IV. Görüntü kümesinin en küçük elemanı -3'tür.
V. Üç tane sıfırı vardır.
ifadelerinden hangileri doğrudur?
yarıçap
M
TANIM
Nümesp
Aşağı
grafiğ
xelisen
SA
Garint
Home
ne
f(x)'in
ve b.
Bun
Cisco
E

Lise Matematik
Fonksiyonun Grafiğiyon-
2 √ + (x) €3-2
f(x) = (x+2) =3
10.x < -2 olmak üzere,
: f(x) = x² + 4x + 1
fonksiyonu veriliyor.
+3
(x + 2) ²3
olduğuna göre, f'(x) aşağıdakilerden hangisi-
dir?
A) -2-√x+3 B) -2+√x+2 C) 3-√x+2
D) 2-√x+3
E) 2+√x+3
f (x) = (x+2) ²/3
√√x+3=yez ²
2
www

Lise Matematik
Fonksiyonun GrafiğiTYT/Temel Matematik
13. m, n, p ve r gerçel sayılar olmak üzere
mx+n
f(x) =
px+r
sabit fonksiyon ise m r = np eşitliği sağlanır.
a ve b gerçel sayılar olmak üzere
f(x)=
A) 1
a+b
3-x
+b
(3-X)
sabit fonksiyon olduğuna göre,
B)
a+b+b(3-x)
2
²3
C) -
b
kaçtır?
D)-3
E)-1
Lise Matematik
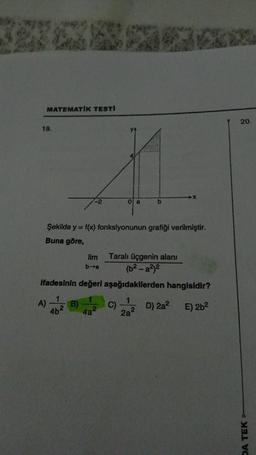
Fonksiyonun GrafiğiMATEMATIK TESTİ
18.
A)
-2
B)
Şekilde y = f(x) fonksiyonunun grafiği verilmiştir.
Buna göre,
lim
ba
4a
0 a
ifadesinin değeri aşağıdakilerden hangisidir?
1
46²
E) 2b²
b
Taralı üçgenin alanı
(b²-a²)²
C)
1
2a²
D) 2a²
20.
DA TEK
Lise Matematik
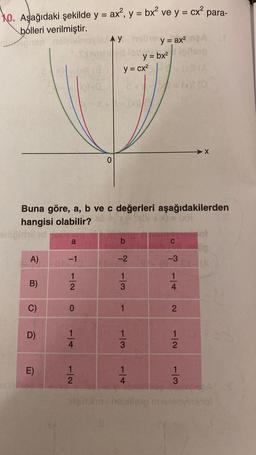
Fonksiyonun Grafiği10. Aşağıdaki şekilde y = ax², y = bx² ve y = cx² para-
bolleri verilmiştir.
A)
B)
C)
D)
E)
a
CLE
Buna göre, a, b ve c değerleri aşağıdakilerden
hangisi olabilir?
-1
1
2
O
114
7|2
Ay math
0
y = cx²
b
-2
w/1
1
13
y = ax² BA
y = bx²
1
4
C
-3
-14
2
1/2
(2)1(A)
(x) (0
13
-X
ot
ilgiminev hebsite ensinovicino)

Lise Matematik
Fonksiyonun Grafiğiu
3. f(x+2) = 3
f(x+2) = 1
(X=-2
7. f(x) = x² - ax + 7 fonksiyonunun grafiği 3 birim sağa
ve b birim yukarıya ötelenerek, g(x) = x² - 11x + 40
fonksiyonunun grafiği elde ediliyor.
Buna göre, a.b çarpımı kaçtır?
A)-45
B)-30
C) 15
D) 30
E) 45
Diğer sayfaya geçiniz
![1. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
-4
olabilir
Buna göre,
|fx-1|=1
3
-2
1. (gof)(a) = a dir.
(fog)(h) = htir
y
2
7
3
Fonksiyon Uygulamaları
f(-58-3
[(-u) = ?
flat=0
denkleminin çözüm kümesi kaç elemanlıdır?
A) 5
B) 6
D) 8
y = f(x)
1x 2140
2. y = f(x) ve y = g(x) fonksiyonlarının grafikleri
y=x
doğrusuna göre simetriktir.
Buna göre,
3. Aşağıda y
y = f(x) fonks
A) X=(-4,0)
f(-2) = -1 alabilir B) X= (0,4) is
ola-3) = f(3)
D) X=(3,5) ise
78
E)
X=[-4,6] is
(10)=
E) g
(H1)=2 lab
f127-3
-4
olabir
30000000
(f(3) = 201²
O
da.
2019/AYT
Flu)= 24. Dik koordinat düzi
yonunun grafiği ve](https://media.kunduz.com/media/question/seo/raw/20230206003142806989-4392066.jpeg?w=256)
Lise Matematik
Fonksiyonun Grafiği1. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
-4
olabilir
Buna göre,
|fx-1|=1
3
-2
1. (gof)(a) = a dir.
(fog)(h) = htir
y
2
7
3
Fonksiyon Uygulamaları
f(-58-3
[(-u) = ?
flat=0
denkleminin çözüm kümesi kaç elemanlıdır?
A) 5
B) 6
D) 8
y = f(x)
1x 2140
2. y = f(x) ve y = g(x) fonksiyonlarının grafikleri
y=x
doğrusuna göre simetriktir.
Buna göre,
3. Aşağıda y
y = f(x) fonks
A) X=(-4,0)
f(-2) = -1 alabilir B) X= (0,4) is
ola-3) = f(3)
D) X=(3,5) ise
78
E)
X=[-4,6] is
(10)=
E) g
(H1)=2 lab
f127-3
-4
olabir
30000000
(f(3) = 201²
O
da.
2019/AYT
Flu)= 24. Dik koordinat düzi
yonunun grafiği ve

Lise Matematik
Fonksiyonun Grafiği4
14. ax² + bx + c = 0 denkleminin kökler toplamı
şeklinde hesaplanır.
Uygun koşullarda tanımlı f ve g fonksiyonları için
f(x) = ax + 2
g(x-a)=f(1-x)
A) 2
1
1-ax+23-ax
xanthop store my
8(04
b
g(a) = x
eşitlikleri sağlanıyor.
3
Buna göre, g(2a) = 0 eşitliğini sağlayan a gerçel
sayılarının alabileceği değerler toplamı kaçtır?
B)-1/2- -D)-1
C)
3-ax=0
E) -/-
3
eg

Lise Matematik
Fonksiyonun GrafiğiÖRNER
f(x)=x²-3x + 8
keser.
0 Diodeteg
parabolü üzerindeki bir noktanın koordinatları toplamının
alabileceği en küçük değer kaçtır?
ÇÖZÜM
Istenen nokta A(x, x²-3x + 8) olsun.
Toplam: x + x²-3x + 8
Tix)=x²- 2x + 8 bulunur.
Toplamın en küçük değeri T(x) fonksiyonunun tepe noktasının
ordinatıdır.
2
1= 2
:1
k=T(1)=1-2+8= 7 dir.
ÖRNEK
Pint
Aşağ
OAT
Lise Matematik
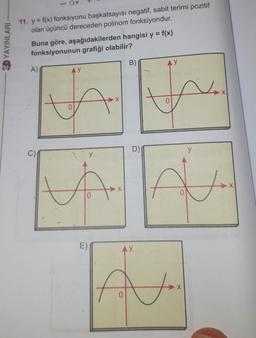
Fonksiyonun Grafiği3D YAYINLARI
ax
11. y = f(x) fonksiyonu başkatsayısı negatif, sabit terimi pozitif
olan üçüncü dereceden polinom fonksiyondur.
A)
Buna göre, aşağıdakilerden hangisi y =
fonksiyonunun grafiği olabilir?
0
E)
X
B)
= f(x)
N
D)
$
Ax
fox

Lise Matematik
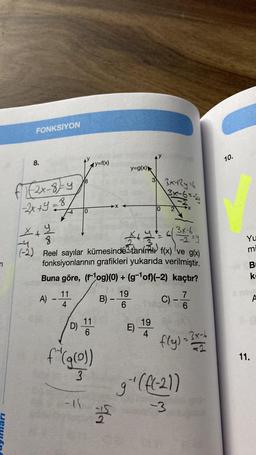
Fonksiyonun Grafiği2.
f bire bir fonksiyon olmak üzere,
f(x2-x)=2x²-2x+3
g(x+2)=x+2
HI.h(x)*
olduğuna göre, (fogogog)(x) fonksiyonu aşağıdaki-
lerden hangisidir?
A) X+4
fenkelyon
D) x+2
=(x1
top snuğublo
B) 2x+4
19 (3
E) x+1
C) 2x+3
3+xS=(S-X)D
•
enöp anuğublo
e
f(g(g (g(x)))
Yay
Lise Matematik
Fonksiyonun Grafiğin
FONKSİYON
8.
F1 (2x-8)=-4
-2x +9=
8
(-2
A)
-
11
4
D)
18
0
x+y
8
X+
+ 1 = 6
3
Reel sayılar kümesinde taním f(x) ve g(x)
fonksiyonlarının grafikleri yukarıda verilmiştir.
Buna göre, (fog)(0) + (g-¹of)(-2)
kaçtır?
-15
11
6
f"(g(0))
3
y=f(x)
B) -
54
y=g(x)
19
6
33x+2y=6
E) 19
0
3x-6=-24
3x-6
-2=y
C) - 7/7/20
6
3x-6
fly) = ?
g¹(f(-21)
-3
10.
Yu
mi
B
ki
11.
A
![28218222
A) 54
Ay
6
60
26. Dik koordinat düzleminde, tanım kümeleri [0, 15] ara-
lığında olan f ve g fonksiyonlarının grafikleri verilmiş-
tir.
3
A) Yalnız I
-2
-4
0 24
C) 64
712
D) I ve II
D) 72
6
y = g(x)
15
ifadelerinden hangileri doğrudur?
B) Yalnız II
>X
y = f(x)
Buna göre,
1. f(x) > g(x) şartını sağlayan 6 farklı tam sayı vardır.
II. f(x) - g(x)| değeri en çok 5'tir.
III. f(x) g(x) = 0 şartını sağlayan 4 farklı x değeri var-
dır.
E) 75
E) I ve Ill
C) Yalnız III
28
23](https://media.kunduz.com/media/question/seo/raw/20230206155730294879-4270653.jpeg?w=256)
Lise Matematik
Fonksiyonun Grafiği28218222
A) 54
Ay
6
60
26. Dik koordinat düzleminde, tanım kümeleri [0, 15] ara-
lığında olan f ve g fonksiyonlarının grafikleri verilmiş-
tir.
3
A) Yalnız I
-2
-4
0 24
C) 64
712
D) I ve II
D) 72
6
y = g(x)
15
ifadelerinden hangileri doğrudur?
B) Yalnız II
>X
y = f(x)
Buna göre,
1. f(x) > g(x) şartını sağlayan 6 farklı tam sayı vardır.
II. f(x) - g(x)| değeri en çok 5'tir.
III. f(x) g(x) = 0 şartını sağlayan 4 farklı x değeri var-
dır.
E) 75
E) I ve Ill
C) Yalnız III
28
23

Lise Matematik
Fonksiyonun Grafiği10. f doğrusal fonksiyon olmak üzere; f(1) + f(2)=31
f(x)+f(x+1)=2x+1
f24f13)=5
hepiecpaly nex919128
olduğuna göre, f(1)+f(2)+f(3)+...+f(10) ifadesinin
değeri kaçtır?
A) 60
B) 55
C) 50
eis
Yayınlan
D) 45
E) 40

Lise Matematik
Fonksiyonun GrafiğiTARAT-ZLE
TARAT-IZLE
Örnek-59
Uygun koşullar altında tanımlanan y = f(x) fonksiyonu için,
lim f(x) = 5'tir.
X-4
Buna göre,
P(x)-25-
lim
x-4 F(x)-21(x)-15
limitinin değeri kaçtır?
lim
X44
+214)-25
+14)-2414)-15
TEME
90 GÜNDE AYT MATEMATİK VIDEO DE

Lise Matematik
Fonksiyonun Grafiği16. f ve g fonksiyonları için,
g: IR→IR, g(x) = 2x + 3
f: Z → Z, f(x) =
(x+ 2 ; x asal sayı ise
x² + 1; x asal sayı değil ise
şeklinde tanımlanıyor.
Buna göre,
(g-¹of)(1) + (g-¹ of) (2)
sonucu kaçtır?
A) 0
B) 2
C) 4
D) 5
E) 6
