İkinci Dereceden Bir Bilinmeyenli Denklemler Soruları

10. Kökleri x² - 6x + 8 = 0 denkleminin kökler top- lamı ile kökler çarpımını kök kabul eden ikinci dereceden denklem aşağıdakilerden hangisi- dir? A) x²-x-4 = 0 C) x² - 14x - 48 = 0 B) x² - 14x + 24 = 0 D) x² - 14x + 48 = 0 E) x² + 14x + 48 = 0

6. y = 2x² parabolü üzerindeki her noktadan x eksenine dikmeler çizilip, çizilen dikmelerin orta noktaları işa- retleniyor. Buna göre, işaretlenen noktaların geometrik yer denklemi aşağıdakilerden hangisidir? x² A) y=- B) y = C) y = x² 4 2 E) y = 4x² D) y = 2x² (19 endemik ........

tir? 0-8 a+b = 2 a.b= 2m₁5 15. x² - 2x + 2m + 5 = 0 denkleminin kökleri a ve b'dir. a²-ab- 2b² = 22 b²-2b+ab=0 olduğuna göre, m değeri kaçtır? A)-4 B)-5 C) -6 D) -8 E)-10 a ²-2a=-2m-5 (x+9) (2-11) x²-2x-95 a (a-2) = -a.b 2 2b-b a-2=-b a = 2-b ib 4-46 +6²-(2-6), b +18²+36-2/16² 22 -99-2m+5 a=11 b=-9

13. a, b ve c birer tam sayı olmak üzere, ax² + bx + c = 0 ikinci dereceden denklemi veriliyor. Buna göre, b² - 4ac ifadesinin değeri aşağıda- kilerden hangisi olabilir? A 2018 B) 023 C2026 D) 2027 74 16 E) 2028 O 15

İKİNCİ DERECEDEN DENKLEMLER 10. x²-3x-5=0 ILARI denkleminin kökleri x, ve x₂ olmak üzere, 1 1 olan ikinci dereceden denklem aşağı — ve X₁ x2 dakilerden hangisidir? A) x² - 5x-3 = 0 B) 3x² - 5x-1=0 C) 5x² + 3x - 1 = 0 D) 5x²-3x-1=0 11. x²-2x-6-0 E) 3x² + 5x - 1 = 0 dir.

Soru 5: x²-x+2=0 denkleminin köklerinin her birinin 2 katının 1 eksiğini kök kabul eden ikinci dereceden denklem aşağıdakilerden hangisi olabilir? A) x² + 3 = 0 B) x² + 5 = 0 C) x² +7=0 D) x² + 9 = 0 E) x² + 11 = 0

18. Gerçek sayılar kümesinde tanımlı f fonksiyonu, ikinci dereceden bir fonksiyondur. f(x-2) <0 eşitsizliğinin çözüm kümesi (-1,6)'dır. Buna göre, f(x). (x²-36) <0 x+2≥0 eşitsizlik sistemini sağlayan x tam sayılarının toplamı kaçtır? A) -15 B) -9 C) -4 D) 5 E) 7

L) I, II ve II 2. f(x)=x² + mx + n fonksiyonu için f(-1)-f(1) < 0 dir. Buna göre, 1. x² + mx + n = 0 denkleminin köklerinden sadece bir tanesi (-1, 1) aralığındadır. II. x² + mx + n = 0 denkleminin kökleri x, ve x₂ ise -1 < x₁ < 1< x₂ dir.- III. m² > 4n dir. ifadelerinden hangileri kesinlikle doğrudur? A) Yalnız I B) Yalnız II D) I ve II E) I ve III C) Yalnız III

- 10. 4x2 - (3m - 1)X + 9 = 0 denkleminin köklerinin geometrik ortalaması, aritmetik ortalamasına eşit olduğuna göre, m'nin alacağı değerler farkının pozitif değeri kaçtır? B) 5 A) 4 C) 6 D) 7 E18 E) 8 Im - | Im-1 3 ml

4. Aşağıda y = x² - b² ve y = -2x² + a parabolleri veril- miştir. AY A 39 y=x²-b² 237 B >X y = -2x² + a 23 C 12 = -b 2 Parabollerin eksenleri kestiği A, B, C ve D nokta- ları birleştirildiğinde oluşan ABCD dörtgeninin ala- ni 24 birimkare olduğuna göre, b kaçtır? 9+8+ A) 2 B) 3- C) 4 D) 5 E) 6 O D 2

Lisesi Analitik Geometri-1 =(- 18. Analitik düzlemde d doğrusunun grafiği çizilmiştir. ABC bir üçgen DC = 2BD AY A(4, 14) les X B(-3, 1) C(3, 4) 4 birimdir? E) 9 Buna göre, d doğrusunun denklemi aşağıdakiler- den hangisidir? A) 2x – 3y - 12 = 0 B) 3x - 2y + 12 = 0 C) 3x + 2y - 12 = 0 D) 3x - 2y - 12 = 0 E) 3x + 2y + 12 = 0 +

x2+bx+c = 0 denkleminin b ve c katsayılarını belirlemek için hilesiz bir zar iki kez atılıyor. Zarin üst yüzünde ilk atışta elde edilen değer b katsayısını, ikinci atışta elde edilen değer ise c katsayısını belirliyor. Buna göre, oluşan denklemin tüm köklerinin gerçel olma olasılığı kaçtır? C) AÎ A) B) -10 5 12 1 2 12 19 23 E) D) 36 36

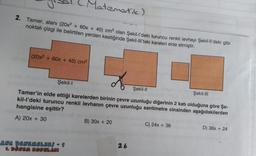
Matematik) 2. Tamer, alanı (20x² + 60x + 45) cm2 olan Şekil-l'deki turuncu renkli levhayı Şekil-Il'deki gibi noktalı çizgi ile belirtilen yerden kestiğinde Şekil-III'teki kareleri elde etmiştir. (20x2 + 60x + 45) cm2 Şekil-1 Şekil-11 Şekil-III Tamer'in elde ettiği karelerden birinin çevre uzunluğu diğerinin 2 katı olduğuna göre Şe- kil-I'deki turuncu renkli levhanın çevre uzunluğu santimetre cinsinden aşağıdakilerden hangisine eşittir? A) 20x + 30 B) 30x + 20 C) 24x + 36 D) 36x + 24 ANA DENEMELERİ - 1 9. DÖNEM KONULARI 26

(3) *1-1 le xli 10. Aşağıda kapağının eğri olan kısmı parabol biçiminde olan ve yüksekliği 25 birim, genişliği 12 birim olan bir termosun kapağı açık ve kapalı durumda iken yandan görünümü verilmiştir. 12. A 9-5.75 gark=5 259 tko ko sa -iban 5 ((x - 55th A 10 B 25 15 12 jo h Şekil 1 Şekil 2 Şekil 1'de termosun kilit çengelinin kapak üzerinde bağlı olduğu nokta C olmak üzere CD 1 AB, CDI = 5 birim ve |DB| = = 10 birimdir. Kapak, Şekil 2'deki gibi açıldığında BA' uzunluğu yer düzlemine paralel olduğuna göre; kapağın tepe Aoktasının yer düzlemine uzaklığı h kaç birimdir? A) 5 B) 6 C) 7 D) 8 E) 9 UcDort

1. Kökleri x ve x2 olan ikinci dereceden denkle- min kökleri arasında, . xx thx thea 2 - (x, +4)· (x2 + 4) = 12 (x,-6). (x2 - 6) = 18 Xx2 - 6x -67 bağıntıları bulunduğuna göre, bu denklem aşa- ğıdakilerden hangisidir? A) x2 – 5x – 24 = 0 B) x - 7x - 24 = 0 C) x² – 5x – 48 = 0 D) 5x + 7x – 48 = 0 E) 5x² – 7x – 48 = 0 C-4b C 4b a ho a 2 C +-216

3 32-4a -30-6 16 +12 - 5. - 2 2 2x² – (3 –a) ·x-c=0 10- 43670X- ikinci dereceden denkleminin köklerinden biri -4, x + (6 + 2)x – d= 0 ikinci dereceden denkleminin köklerinden biri 2 dir. bx + 2x2 25.4 Bu iki denklemin diğer kökleri eşit olduğuna göre, a - 2b farkı kaçtır? - A) 7 B) 12 C) 15 D) 16 E) 19 16+ 12 28-40-c=0 8+2b.d = 0