İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri Soruları

a ayırır. eleştirilmesi ile ilgili işlemleri yapar. Adı Soyadı: en değiştirme, rasyonel ifade ANLARA AYIRMA Örnek 2 nlara el bir yön- (2x + y) 3y - 5x - (2x + y) ifadesini çarpanlarına ayırınız. Çözüm Bilgi Kutusu Örnek 3 x-y=-(y-x) (x - y)²n = (y - x)²n (x - y)²n + 1 = -(y - 3a (m-n)-2b-(n-m)

X 2. Harun bir işin yarısını 6 günde Harun aynı işi birlikte 4 günde yapabilmektedir. Ayşe ve yapabilmektedir. Buna göre, Harun'un çalışma hızının Ayşe'nin çalış- ma hızına oranı kaçtır? A) 2/2/2 B) / C) D) 1/14 9²3 is

9. SINIF SARMAL MATEMATİK 112 sayilardir B) a ve b çift sayılardır. C-a çift, b tek sayıdır. D) a - b tek sayıdır. E) a + b tek sayıdır. a ve D -gift ile D) a³-16 4 tf 32 3. a çift sayı olduğuna göre, aşağıdakilerden hangisi daima çift sayıdır? A) a² + a +1 B) 222 tek E) af C) a²-a 2 a (a + 1) 2 térk A 5. a = 2020 ve b = a + b toplar II. b²-a² farl III. a.b² ifadelerinden A) Yalnız I 80 çarp D

2) Şekildeki ABC üçgeninin içinde bir D noktası işaretleni- yor ve DBC üçgeni çiziliyor. Bu üçgenlerin özellikleri ile ilgili aşağıdakiler biliniyor. •|AB| = |BC| = |CD| • m (ABD) = m (BCD) = 24° B C Buna göre, m (BAC) kaç derecedir? A) 20 B) 24 C) 30 D) 39 E)

x ve y birer gerçel sayı olmak üzere, 0<x² <16 4< y² <25 n r olduğuna göre, 3x-y ifadesinin alabileceği en bü- yük tam sayı değeri kaçtır? A) 9 B) 16 C) 17 D) 18 E) 19 A² X A) ifadesinin hangisidi y + X²

13 m<n<0<k ve |k|> [m] olmak üzere, A) (-k, m) 1-0 <0 eşitsizliğini sağlayan aralıklar- (x² - m²). (x + n) (x²-K²) dan birisi aşağıdakilerden hangisidir? B) (m, -n) D) (k, +∞0) 47 C) (-n, -m) E) (-k, -n)

O STABILO 26 0063814922 EGOOD MENTERI SENI V TEMI U B B B 2m-b1 11. a bir tam sayı olmak üzere, -8 (x-a) (3x - 13) < 0 eşitsizliğini sağlayan 3 tane x tam sayısı bulunmaktadır. Buna göre, a sayısının alabileceği değerler toplamı kaçtır? A) 5 E) 4 B) 6 4/201 MATEMATİK C) 7 D) 8 =842. (0²- d E) 9

6. f(x)=√x²-3x - 10 - √9-x3 fonksiyonunun en geniş tanım kümesindeki tam sayıların toplamı kaçtır? A) - 7 + 3 > × 2-3 5 -2 5 C) -3 (x-5) (x+2) >0 D) - 1 4- - E) 0 2.10.17 5/16.7 -#fujity 2-titi2, 3,4,5 $SUPARA -92₁10173 9.

y) 2. Dik koordinat düzleminde 3y + 4x ≤ 15 y-1≥0 A) 13 225=90 B) 14 1 eşitsizlikleri veriliyor. Buna göre, bu eşitsizlik sisteminin çözüm kümesini oluştu- ran kapalı bölgenin çevresi kaç birimdir? C=25 C) 15 b) 16 E) 17 4.

6. x ve y gerçel sayılar olmak üzere, dik koordinat düzleminde 3≤x≤9 4x 3 y≤. y≥x eşitsizlikleri veriliyor. Buna göre, bu eşitsizliklerin tümünü sağlayan kapalı bölge aşağıdaki geometrik şekillerden hangisini oluşturur? A) Yamuk C) Dik üçgen E) Kare B) Dikdörtgen D) Üçgen

a tam sayı olmak üzere, (x-a) (x+2) 9. X-0 =0 XmX=C vitiepel endapob eşitsizliğinin çözüm aralıklarından biri (−1, 3) aralığıdır. Buna göre, a kaçtır? A) -3 ● X-3 <0 <One B)-2 ST-0 X42=0 X2-2 C) -1 D) 1 E) 2 ka 11

1. Aşağıdaki şekilde, a Y C TVS ( ANALY işlemi tanımlanıyor. Buna göre, A) X-5 X+2 +2 D) +² b x+3 x-1 4x-5 x²-4 x²+x-6 B) 2x-3 a+b C ifadesinin en sade hâli aşağıdakilerden hangisidir? x + 3 X+2 X+5 omgeblo (ev vsa legrop ix 01-2 They police 0150 AUS (8 X 1(4) x+23100) E) X-5 X-2 C)

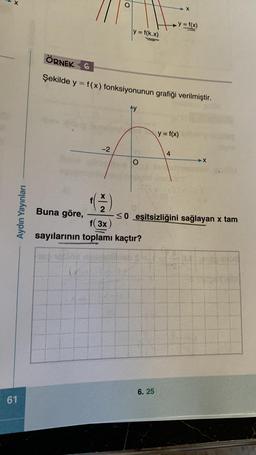
61 Aydın Yayınları O -2 Buna göre, y = f(k.x) ÖRNEK 6 Şekilde y = f(x) fonksiyonunun grafiği verilmiştir. ty RA *(*) f(3x) sayılarının toplamı kaçtır? 6.25 X y = f(x) y = f(x) 4 ≤0 eşitsizliğini sağlayan x tam

6. Aşağıda farklı hacimlerde iki sürahi ve iki farklı bardak ve- rilmiştir. Başlangıçta boş olan sürahilere, şekilde verilen bardaklarla belirli bir miktarda su doldurulacaktır. 1. sürahi ● 2. sürahi st x ml 1. bardak C) 24 4+ Bu işlem için aşağıdaki bilgiler verilmiştir. 2. sürahinin hacmi, 1. sürahinin hacminden da daha fazladır. Bardakların tamamı dolu olmak şartıyla 1.sürahiye 1.bardak ile 4 defa, 2.bardak ile 5 defa su dolduruluyor. Bardakların tamamı dolu olmak şartıyla 2.sürahiye 1.bardak ile 8 defa, 2.bardak ile 6 defa su doldurulu- yor. y ml D) 26 2. bardak Son durumda 2. sürahideki su miktarı, 1. sürahideki su miktarından 32 ml fazla ve 2. sürahideki boş kısmın, 1. sürahideki boş kısma oranı olduğuna göre, x + y toplamı kaçtır? A) 18 B) 20 oranın- E) 28

-11²+64-20 46 -t' +2st - 80 £²-24€+80 £ 2. Neden ( ile bapladne? -4 -20 -2 AY + (4620) Z D) III ve V 4 -2 + 5 20 y = g(x) Yukarıdaki şekilde y = f(x) ve y = g(x) fonksiyonlarının grafikleri verilmiştir. y = f(x) doğrusu x eksenini (3,0) noktasında, y = g(x) parabolü ise (-2,0) ve (5,0) nok- talarında kesmektedir. y = f(x) f(x) Buna göre, ≤0 eşitsizliğinin çözüm kümesi g(x) X=-2 X=5 1. (-∞, -2) II. (-2, 3] III. (-2, 3) IV. (3,5) V. (5,00) + luxo lish 3 5 aralıklarından hangilerinin birleşim kümesidir? A) I ve II B) I ve III C) II ve V E) Ill ve V Testokul LO 5 6

n, 2 (a +2) W b) Örnek-11 Denklem Eşitsizlik Sistemleri a) (x-2). f(x) ≤0 [32] O Ay g(x) x²-2x-3 y = g(x) Yukarıda y = f(x) ve y = g(x) fonksiyonlarının grafik- leri verilmiştir. MO 2 Buna göre, aşağıdaki eşitsizliklerin çözüm kü- mesini bulunuz. y = f(x) 4 g(x) (x-3)(x+1₂) c) f(x). g(x) (x² + 3x) ≤0 ≥0