İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri Soruları

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriX E F
D X
X C
T
H x G
4
L
D) (3, 7)
2x
K
2x+6
1. tabela
2. tabela
İki
dikdörtgenden oluşan 1. tabela ve dik üçgenden oluşan
2. tabela, Galip Usta tarafından boyanacaktır. Galip Usta,
boyadığı alana göre ücret almaktadır.
IADI = IDEI = IFC| = |HG| = x br
IEHI = 4, IKLI = 2x, IKMI = 2x+6 br
Galip Usta, 2. tabeladan daha fazla ücret aldığına göre;
x'in en geniş değer aralığı aşağıdakilerden hangisidir?
A) (0, 2)
B) (1,4)
C) (2,5)
M
E) (0,4)

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri24
=2
101
12. -2+ x + 2) = 4
50
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisi.
dir?
A)
2=2 B)<
7. E
C) -
D) A
4 ü veriyo
her zaman bu aralık
E)
8. B
-2
-2
-2
-2
-2
9. E
10. D
2
62
2
2
2
11. D
103
12. A
www.fenbilimleriyayinlari.com
3.
-pa
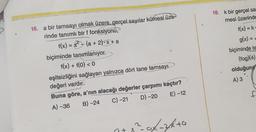
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri16. a bir tamsayı olmak üzere, gerçel sayılar kümesi üze-
rinde tanımlı bir f fonksiyonu,
f(x) = x²(a + 2).x+ a
biçiminde tanımlanıyor.
f(x) + f(0) <0
eşitsizliğini sağlayan yalnızca dört tane tamsayı
değeri vardır.
Buna göre, a'nın alacağı değerler çarpımı kaçtır?
D)-20
C) -21
A) -36
B) -24
E) -12
2-01-2/x+9
n+ x
18. k bir gerçel sa
mesi üzerinde
f(x) = k-
g(x) = ₁
biçiminde ta
(fog)(4)
olduğuna
A) 3

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri14.
V=g(x)
<0
2
y=f(x)
Şekilde f, g ve h fonksiyonlarının grafiği verilmiştir.
Buna göre,
y=h(x)
A) (-3) U (0, 1) B)(0)
D) (-3,0) 1. ∞)
f(x)-f(x)
g(x)
eşitsizliğ hin çözüm kümesi aşağıdakilerden hangisi-
dir?
MATEMATİK
C) (-3,-1) U (0, 1)
E) (0)
✔FEN BİLİMLERİ YAYINLARI
C
17

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerisidir?
(4,00)
(2,00)
TEN SORULAR
10. a<0<b olmak üzere,
ax-b
bx + a
A) -
->0
C) R
a
eşitsizliğinin çözüm kümesi aşağıdakilerin hangisidir?
a b
b'a
b
a
to:-0
a b
a
b
......
b=t
E) -51
a
.......
(65) (0
B)
of
a
9
a
b
ba
a'b

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri4.
-2
Buna göre,
0
1
B) 2
y=f(x)
2
X
Yukarıda y = f(x) ve y = g(x) fonksiyonlarının grafikle-
ri verilmiştir.
y=g(x)
f(x) g(x) > 0
eşitsizliğini sağlayan x tam sayıları kaç tanedir?
A) 1
C) 3
D) 4
E) 5

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriDENEME
24.
10
1. mum
2. mum
Şekilde gösterilen özdeş iplerini kalın ip, ka-
lan kısmı ince iptir.
5
İki farklı yanma kapasitesine sahip mumların,
ince ve kalın ipleri yakma hızları aşağıdaki tab-
loda verilmiştir.
İnce ip
Kalın ip
MATEMATIK
1. mum
5 cm/sn.
4 cm/sn.
+1²
2. mum
6 cm/sn.
5 cm/sn.
1. mum ipin tamamını, 2. mumdan 36 sn. daha
geç yakmıştır.
Buna göre, bir ipin uzunluğu kaç metredir?
A) 650 B) 720 C) 800 D) 860 E) 900
25
QÖZDEBİR YAYINLARI
2

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerier rakam olmak üzere,
ISının çift sayı olduğu,
ısının 5'in tam katı olduğu,
ISının 9 ile tam bölündüğü
Csayılarının tamamı ayrı ayrı
3.
rcq
x(x-3)(x - 5) < 6(x-3)
eşitsizliğini sağlayan pozitif x tam sayılarının toplamı
6ea1Y
x=3
kaçtır?
A) 12
B) 11
C) 10
6x-18 = 9
X=0
D) 9
E) 8
tematik
atematik

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriDOĞRU BİLGİ
Rasyonel İfadeler
P(x) ve Q(x) birer polinom ve Q(x) = 0 olmak üzere, şeklin
rasyonel ifadeler denir.
Rasyonel ifadelerle toplama, çıkarma, çarpma ve bölme işlemleri
larda olduğu gibi yazılır.
Örnek-1
x² - 4x + 3 3x²-x-4
x²-1 x²-x-6
ifadesinin en sade biçimini bulunuz?
Çözüm:
DEĞERLENDİR
Örnek - 2
DEĞERLENDİR
P(x)
Q(x)
ax² - ay²
ax + ay
ifadesinin en sade biçimini bulunuz?
40 Serisi Ⓡ
S

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri13
5.
6.
A) √√3
x²+x+1
x²-4
B) √5
(3-X).3x-1
x²-1
<0
eşitsizlik sistemini sağlayan x değerlerinden biri aşa-
ğıdakilerden hangisi olabilir?
C) √10
mx-4
X+n
>0
C) 8
≤0
10g au
eşitsizliğinin çözüm kümesi
m.n+ n² ifadesinin değeri kaçtır?
A) 0 B) 4
D) 2√3
E) 4
4,3 olduğuna göre,
SD) 12
2.
bolld
E) 16
Diğer Sayfaya Geçiniz
iyin
jay
yin
ir
niz

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri9. Bir üniversitede öğrenciler bir dönemde her dersten ara sınay
ve final sınavı olmak üzere iki sınava girmektedirler.
Öğrencinin, dönem sonu notu hesaplanırken ara sınavın
%40'ı final sınavının ise %60'ı alınarak bulunan değerler top-
lanmaktadır. Dönem sonu notu 45'in altında olanlar dersten
kalmakta 45 ve üzeri olması durumunda dersten başarılı sa-
yılmaktadır.
Aşağıdaki tabloda aynı dersi olan iki öğrencinin her biri tam
sayı olan ara sınav ve final sınavı notlarının bazıları verilmiştir.
Ara Sınav
Final Sınavı
20
Anıl
Veysel
a
Anıl dersten kalmış Veysel ise dersten geçmiş olduğuna
göre, b - a farkının en büyük değeri kaçtır?
A) 38
B) 37
C) 35
D) 32
b
60
E) 29

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerikiler-
40/
13. (4-2x)*. √8-x ≤0
eşitsizliğini sağlayan x tam sayı değerlerinin
toplamı kaçtır?
A) 14 B) 16 C) 18 D) 20 E) 25
urina Buring
e gönderildiği
war gemidler
Bodrumdalu sünger avci-
Bodrumu eserlerinde
Ulican

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri3.
√
A) R - {2}
+
-00
(m - 2)x² - (m+1)x - 1 <0
eşitsizliği tüm x reel sayıları için sağlandığına göre, m
nin çözüm aralığı aşağıdakilerden hangisidir?
D) (-7, 2)
B) R - (-7, 1)
+
E) (-7, 1)
C) (1, 2)
final eğitim kura
7.
(16-x²)
x²-7x-
eşitsizliğ
A) 3
![3.
2.
1.
2.
1.
11. SINIF
Bu testte 30 soru vardır.
Cevaplarınızı, cevap kâğıdının Matematik için ayrılan kısmına işaretleyiniz.
A) (,0)
C) [1.3)
x²(x-1)
3-x
eşitsizliğinin çözüm kümesi aşağıdakilerden hangi-
sidir?
E) (,0) [1, 3)
x² - 6x +5
(x+3)²
20
11. Sınıf Deneme 5-2201/05
-<0
eşitsizliğini sağlayan farklı x tam sayı değerlerinin
toplamı kaçtır?
A) 8 B) 9
(x-1)2022 (2-x) 01
(x+1)³. (x²-9)
MATEMATİK
B) (0] [1.3]
D) [1, 3) (0)
C) 3
C) 10 D) 12 E) 15
-20
eşitsizliğini sağlayan kaç farklı x tam sayı değeri
vardır?
A) 1 B) 2
D) 4
E) 5
13
5.
6.
A)-3
B
(x²+x+1)(x² +9)
(3-x)(x+1)
eşitsizliğini sağlayan x tam sayı değerlerinin toplamı
kaçtır?
B)-1 C) 1 D) 2 E) 3
A) √3 B) √5
20
x²+x+1 <0
x²-4
(3-X).3*-1
x²-1
eşitsizlik sistemini sağlayan x değerlerinden biri aşa-
ğıdakilerden hangisi olabilir?
C) √10 D) 2√3 E) 4
mx-4
x+n
->0
so
,3 olduğuna göre,
eşitsizliğinin çözüm kümesi
m.n+n ifadesinin değeri kaçtır?
A) 0 B) 4 C) 8 D) 12 E) 16
Diğer Sayfaya Geçiniz
in kullanılabilin](https://media.kunduz.com/media/question/seo/raw/20230311082306521518-4618634.jpeg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri3.
2.
1.
2.
1.
11. SINIF
Bu testte 30 soru vardır.
Cevaplarınızı, cevap kâğıdının Matematik için ayrılan kısmına işaretleyiniz.
A) (,0)
C) [1.3)
x²(x-1)
3-x
eşitsizliğinin çözüm kümesi aşağıdakilerden hangi-
sidir?
E) (,0) [1, 3)
x² - 6x +5
(x+3)²
20
11. Sınıf Deneme 5-2201/05
-<0
eşitsizliğini sağlayan farklı x tam sayı değerlerinin
toplamı kaçtır?
A) 8 B) 9
(x-1)2022 (2-x) 01
(x+1)³. (x²-9)
MATEMATİK
B) (0] [1.3]
D) [1, 3) (0)
C) 3
C) 10 D) 12 E) 15
-20
eşitsizliğini sağlayan kaç farklı x tam sayı değeri
vardır?
A) 1 B) 2
D) 4
E) 5
13
5.
6.
A)-3
B
(x²+x+1)(x² +9)
(3-x)(x+1)
eşitsizliğini sağlayan x tam sayı değerlerinin toplamı
kaçtır?
B)-1 C) 1 D) 2 E) 3
A) √3 B) √5
20
x²+x+1 <0
x²-4
(3-X).3*-1
x²-1
eşitsizlik sistemini sağlayan x değerlerinden biri aşa-
ğıdakilerden hangisi olabilir?
C) √10 D) 2√3 E) 4
mx-4
x+n
->0
so
,3 olduğuna göre,
eşitsizliğinin çözüm kümesi
m.n+n ifadesinin değeri kaçtır?
A) 0 B) 4 C) 8 D) 12 E) 16
Diğer Sayfaya Geçiniz
in kullanılabilin

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriÖrnek:
²-9
(x - 2)²
eşitsizliğini sağlayan kaç tane x tamsayısı vardır?
C) 7
A) 5
SO
B) 6
Örnek:
(x+4)².(6-x)²2 <0
x² - 4
eşitsizliğin çözüm kümesi nedir?
A) (-2,2)
B) (-4,-1, 0, 1, 6)
C) (-4, 6)
D) x < -2 veya x > 2
E) (-2, 2) (-4, 6}
D) 8
E) 9
Xe
Ora
![4.
B
A) 2/1/12
B) 2b
C) 1
3ª [2] = 30 +3²
a=b=c
3a.2= 344 3 a
A) 3
100(A2) 8
A
AB ve CD iki basamaklı sayılar olmak üzere, dört ba-
samaklı rakamları farklı ABCD sayısının AB ile bölü-
münden bölüm 101 kalan 48'dir.
Rakamları farklı dört basamaklı CEBF sayısı A.C
ile tam bölünebildiğine göre, E kaçtır?
B) 4
C) 6
nos D) 7
G
D) 2
up 48-D
=
= 7-234-2
+++8
26%
a
E) 8
3](https://media.kunduz.com/media/question/seo/raw/20230310094534945995-2032757.jpeg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri4.
B
A) 2/1/12
B) 2b
C) 1
3ª [2] = 30 +3²
a=b=c
3a.2= 344 3 a
A) 3
100(A2) 8
A
AB ve CD iki basamaklı sayılar olmak üzere, dört ba-
samaklı rakamları farklı ABCD sayısının AB ile bölü-
münden bölüm 101 kalan 48'dir.
Rakamları farklı dört basamaklı CEBF sayısı A.C
ile tam bölünebildiğine göre, E kaçtır?
B) 4
C) 6
nos D) 7
G
D) 2
up 48-D
=
= 7-234-2
+++8
26%
a
E) 8
3
