İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri Soruları

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerix² + (2a − 1)x + a − 1 = 0
denkleminin kökleri x₁ ve x₂ dir.
X2
3
Bu köklerin aritmetik ortalaması
oldu-
3
ğuna göre, x³.x₂+x³.x, ifadesinin değeri
2
1
aşağıdakilerden hangisidir?
A) -42 B)-27
5
C) 27
--
2
D) 38 E) 42
![özüm kümesi aşağıdakiler-
B) (-∞, 0) U [2, 4)
D) (2,4)
##
"
5.
x-1
x² - 4
<0
|x+2
X-1
eşitsizlik sisteminin çözüm kümesi aşağıdakiler-
Uden hangisidir?
A) (-2, 1)
C) (-2, 1] U (2,5)
B) (1, 2)
D) (-2, 1] U {2}
E) R-{-2, 2}
1y²-21](https://media.kunduz.com/media/question/seo/raw/20230311065746625781-5135297.jpg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleriözüm kümesi aşağıdakiler-
B) (-∞, 0) U [2, 4)
D) (2,4)
##
"
5.
x-1
x² - 4
<0
|x+2
X-1
eşitsizlik sisteminin çözüm kümesi aşağıdakiler-
Uden hangisidir?
A) (-2, 1)
C) (-2, 1] U (2,5)
B) (1, 2)
D) (-2, 1] U {2}
E) R-{-2, 2}
1y²-21
Lise Matematik
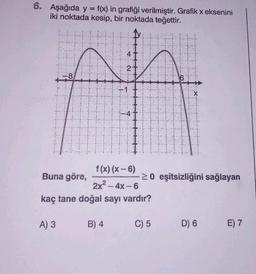
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri6. Aşağıda y = f(x) in grafiği verilmiştir. Grafik x eksenini
iki noktada kesip, bir noktada teğettir.
-8
6
AA
f(x) (x-6)
Buna göre,
2x² - 4x-6
kaç tane doğal sayı vardır?
A) 3
B) 4
20 eşitsizliğini sağlayan
C) 5
D) 6
E) 7

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri7.
x4 <x³ < x²
eşitsizliği veriliyor.
Buna göre, x in alabileceği tüm değerlerin kümesi
aşağıdakilerden hangisidir?
A) (-∞0, 0)
C) (-2, -1)
(1, ∞)
(1, 2)
B) (-1,0) (0, 1)
D) (0, 1)
E) (-∞, -1) U (1,00)
![2
f(x) = (-a²-5a +6)x + 4
fonksiyonunun değişim hızı negatif olduğuna
göre, a'nın en geniş tanım aralığı aşağıdakilerden
hangisidir?
A) (-6, 1)
B) [-6, 1]
D) R-[-6, 1]
C) R -(-6, 1)
E) (-∞, -6)
4KY-
69](https://media.kunduz.com/media/question/seo/raw/20230311012825846441-2878670.jpeg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri2
f(x) = (-a²-5a +6)x + 4
fonksiyonunun değişim hızı negatif olduğuna
göre, a'nın en geniş tanım aralığı aşağıdakilerden
hangisidir?
A) (-6, 1)
B) [-6, 1]
D) R-[-6, 1]
C) R -(-6, 1)
E) (-∞, -6)
4KY-
69

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri13. Erdal Bey işe gitmek için farklı iki yol kullanmaktadır.
1. yolun uzunluğu (x2 + 2x + 20) metre,
2. yolun uzunluğu (5x + 200) metredir.
Birinci yol ikinci yoldan kısa olduğuna göre, x in ala-
bileceği en küçük tam sayı değeri kaçtır?
A)-18 B)-15 C) -14 D) -12 E)-11
x2+2x+20< 5x+200

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri12
n
0
2
A(2, n)
y=(fog)(x)
6
n =
X
fog (2)
n=f(g(21)
y=f(x)
Şekilde y = f(x) ve y = (fog)(x) doğrusal fonksiyonlarının
grafikleri verilmiştir.
Bu iki fonksiyon A(2, n) noktasında kesişmektedir.
Buna göre, f(2) + g(2) toplamı kaçtır?
A) 6
B) 8
C) 10 D) 12
E) 13

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerioplamı
A
17. Aşağıda bir eşitsizlik sisteminde bulunan iki farklı eşitsizliğe ait işaret
tablosu verilmiştir.
A) x²-x-2 <0
2x²10x + 12 > 0
C) -x²-2>0
+
2x²10x + 12 > 0
-1
0
(
IVAMIS
Buna göre, eşitsizliklerin çözümü olarak belirtilen mavi renkli
bölge dikkate alındığında bu eşitsizlik sistemi aşağıdakilerden
hangisi olabilir?
2
0
3. Aşağıda tepe noktası T(132) olon
+
3
E) 2x² - 2x - 4 <0
x2 − 5x − 6 > 0
MATEMATİK
B) x²-x+ 2 ≤0
x – 5X + 6 > X
D) x²-x-2>0
_ Dx−5x+6<0
x2 – 5x + 6 < 0
us

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri18.
A) 9000
SENOL
HOCA
B) 10000
Üçlük
DENEME
Yukarıda bir marangozun toptancıdan alabileceği tahta ka-
liplar ve yanlarında fiyatları gösterilmiştir.
Aynı renkli tahta kalıpların fiyatları da aynıdır.
D) 12000
2500 TL
Buna göre, marangoz toptancıdan 6 tane mavi kalıp, 5
tane kırmızı kalıp ve tahta alırsa kaç TL ödemelidir?
3750 TL
E) 13000
C) 11000

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriX
Jond
II
Kesişim
88
+
1
~
MAS
+
x²-3x > 10
1.0
-x² + 9x ≥ 8
C) x²-3x < 10
-x² + 9x < 8
5
0 Çözüm O
X=-2
+
(X-5)(x+2) <0
+
Yukarıda I ve II eşitsizliklerine ait işaret tablosu veril-
miştir.
Buna göre, çözüm kümesi [1, 5) aralığı olan eşitsiz-
lik sistemi aşağıdakilerden hangisi olabilir?
8
00
E) x² + 3x < 10
-x² + 9x ≥8
+
1
B) x²-3x < 10
-x² + 9x ≥8
D) x²-3x < 10
-x² + 9x ≤ 8

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerieril-
esi
191
C)
D)
E)
f(x)
X
f(x)
X
f(x)
+
C) R -0,
ote
a
91
+
-3
te
3
3
G
6. a<0<b olmak üzere,
x(ax-b) ≤0
eşitsizliğinin çözüm aralığı aşağıdakilerden han-
gisidir?
A) |0. - 1
+
a
B) 0,
D) (-00, 0) (-2, 0)
E) (-∞, -~0,00)
Lise Matematik
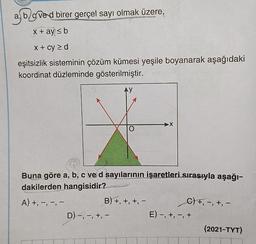
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleriabove d birer gerçel sayı olmak üzere,
x + ay ≤ b
x + cy≥d
eşitsizlik sisteminin çözüm kümesi yeşile boyanarak aşağıdaki
koordinat düzleminde gösterilmiştir.
TOALELASTNINECIENU
AY
D) -, -, +, -
O
Buna göre a, b, c ve d sayılarının işaretleri sırasıyla aşağı-
dakilerden hangisidir?
A) +, -, -, -
B) +, +, +, -
X
C) +, -, +, -
E) -, +, -, +
(2021-TYT)
![asal tor
oda aşa
kolay
Kirg
2
ya
14
sağlanır?
A) -xxaxat
0<a<1
1
2
14. 7a+4b <11
2b-a≤7
0-4
Z
B) 3
E) 10-ak
inde a ca sarti
C) 4
B) -10 <ax-
D) 1×a×10
OR
O
Buna göre a+b toplamının alabileceği en büyük
değer kaçtır?
A) 2
0-la 1
kalırlar.
D) 5
E) 6
16
3ea67
-4sb<5
Yukarıda verilenlere göre ab asagidaki aralıkların
hangisindedir?
A) [-28,35)
[-28.15)
8) (-12.35)
D) (15,35) 6) (-15.28]
17. Aşağıdakilerden hangisi veya hangileri doğrudur?
1) 2<x<5
ise
4<x² <25
11) -7<y≤-3
III) -8 ≤z<4
ise
ise
A) I B) III C) 1,111
9<y² ≤ 49
0≤z² ≤64
D) II,III
E) Hepsi](https://media.kunduz.com/media/question/seo/raw/20230310182251368854-4307842.jpg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleriasal tor
oda aşa
kolay
Kirg
2
ya
14
sağlanır?
A) -xxaxat
0<a<1
1
2
14. 7a+4b <11
2b-a≤7
0-4
Z
B) 3
E) 10-ak
inde a ca sarti
C) 4
B) -10 <ax-
D) 1×a×10
OR
O
Buna göre a+b toplamının alabileceği en büyük
değer kaçtır?
A) 2
0-la 1
kalırlar.
D) 5
E) 6
16
3ea67
-4sb<5
Yukarıda verilenlere göre ab asagidaki aralıkların
hangisindedir?
A) [-28,35)
[-28.15)
8) (-12.35)
D) (15,35) 6) (-15.28]
17. Aşağıdakilerden hangisi veya hangileri doğrudur?
1) 2<x<5
ise
4<x² <25
11) -7<y≤-3
III) -8 ≤z<4
ise
ise
A) I B) III C) 1,111
9<y² ≤ 49
0≤z² ≤64
D) II,III
E) Hepsi

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri1.
A
B
y = x + 1
y=-x²+x+2
Yukarıdaki şekilde y = -x² + x + 2 parabolü ve
y = x + 1 doğrusu verilmiştir.
Buna göre kesiştikleri A ve B noktalarının ap-
sisleri toplamı kaçtır?
A) 0 B) 1 C) 2
D) 3 E) 4
3.
Yuk
mis
Bu
A

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleriin
10.
X
X
(X=2)
(x2 _ 5x+6).(7−x) -≤0
41
-b
x²-1
X=1 X=-1
elipeşitsizliğini sağlayan kaç farklı x tam sayısı var-
dır?
A) 1 B) 2
C) 3
D) 4
E) 5
ange
Sy hebs
hepsivee met erst bil igeelidsis nin m
win
![B
12.
A) Yalnız T
D) I ve III
2x (x3-x²-2x)
x²-1
1
MO
eşitsizliğini sağlayan x gerçek sayılarının çözüm kü-/
mesi aşağıdakilerden
hangisidir?
A) (-1,0]U (1,2]
C) R-[-1,1]
, II ve III
B) [0, 1) U[2,00)
D) [0,2]-{1}
E) (-∞, -1) U[0, 1) U[2,00)
0
x (x²-x-2)
-
2
+1
Ankara Yayıncılık](https://media.kunduz.com/media/question/seo/raw/20230310165547353831-1901058.jpeg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriB
12.
A) Yalnız T
D) I ve III
2x (x3-x²-2x)
x²-1
1
MO
eşitsizliğini sağlayan x gerçek sayılarının çözüm kü-/
mesi aşağıdakilerden
hangisidir?
A) (-1,0]U (1,2]
C) R-[-1,1]
, II ve III
B) [0, 1) U[2,00)
D) [0,2]-{1}
E) (-∞, -1) U[0, 1) U[2,00)
0
x (x²-x-2)
-
2
+1
Ankara Yayıncılık
