İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri Soruları

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleritam sayı
E)-1
6.
A={x|x²-9≤0, x gerçek sayı}
B={x| (x+5)(x-2)>0, x gerçek sayı}
olduğuna göre, B-A kümesinin en küçük pozitif tam
sayı elemanı kaçtır?
A) 1
B) 2
*²950
(x-3) (x+3)(<0
x= 3 x=3
A
3
D
C) 3
B.S-n
D) 4
*+5)(x-2) >0
(x=-1) X=2
2 3
E) 5

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerikümesi aşağıdakilerden
√2), (2, 2)}
2√2,-2), (2, 2)}
2)}
Yanıt Yayınları
5.
a > 1 olmak üzere,
(x²-a²) (ax + 1)
x + a
<0
eşitsizliğinin çözüm kümesi aşağıdakilerden hangi-
sidir?
A) (1, a)
a
D) (a, ∞)
B) (-a, a)
E)
C) (0, a)

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerig(x) f(x)
rinin grati
dakilen
C) (-3)
lit
1.
Aynur ve Mert bir bilgisayar programını kullanarak
x² + 2y² = 12 elipsi ile 2x² - y2 = 4 hiperbolünün grafi-
ğini aşağıdaki gibi koordinat eksenine çizmişlerdir.
2x² - y² = 4
AY
Je
EBA PEKİŞT
x² + 2y² = 12
Buna göre, çizdikleri elips ve hiperbolün ortak nok-
talarının kümesi aşağıdakilerden hangisidir?
A) {(2, 2), (-2, 2)}
B) {(2, 2), (2,-2), (-2, 2)}
c) {(2, 2), (2,-2), (-2,-2), (-2, 2)}
D) {(-2,-2), (2, 2)}
E) {(-2,-2), (2,-2)}
Yanıt Yayınları

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri36
24
G
Seori = 4x
+1 +1
X
(2) (4) (
Cix
D) 30
ECH
19)
Eşit kapasiteli 4 işçi birlikte işe başladıktan 2 gün sonra
birinci işçi ondan 3 gün sonra ikinci işçi işi bırakıyor.
10 günün sonunda iş bitiyor.
Buna göre işçilerden herhangi biri aynı işi tek başıma kaç
günde bitirir?
A) 27 B) 28 C) 29
E) 31
3
23)
Kap
ikiş
İşin
bas
A)
![-1-x²
2. f(x)=x²-x fonksiyonu veriliyor.
2 ≤ f(x) ≤ 6
koşulunu sağlayan x reel sayılarının bulunduğu en
geniş aralık aşağıdakilerden hangisidir?
A) (-1,2)
D) (1, 2)
B) [-2, 1)
C) (-2, 3)
E) [-2, -1) U (2, 3]
eşits
lerde
A
E)](https://media.kunduz.com/media/question/seo/raw/20230302152027008754-3884350.jpg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri-1-x²
2. f(x)=x²-x fonksiyonu veriliyor.
2 ≤ f(x) ≤ 6
koşulunu sağlayan x reel sayılarının bulunduğu en
geniş aralık aşağıdakilerden hangisidir?
A) (-1,2)
D) (1, 2)
B) [-2, 1)
C) (-2, 3)
E) [-2, -1) U (2, 3]
eşits
lerde
A
E)

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri2. x²-mx-n-0 ikinci dereceden denklemi için
Kökleri 3 ten büyük değildir.
m ve n pozitif tam sayılardır.
.
•
şartlan sağlanıyor.
Buna göre, kaç farklı (m, n) sıralı ikilisi vardır?
A) 9
B) 10
C) 12 D) 15 E) 16
Lise Matematik
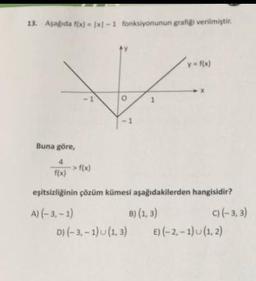
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri13. Aşağıda f(x)= |x-1 fonksiyonunun grafiği verilmiştir.
Buna göre,
-> f(x)
O
f(x)
eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
A) (-3,-1)
C) (-3, 3)
D) (-3,-1) U (1,3)
y = f(x)
B) (1, 3)
E) (-2,-1) U (1, 2)

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri7.
(x=1
8.
côn âm
kümesine
A) 5
Mutlak değerli
bir ifade iaeriyorsa
anun daima
pozitif bir
Sonuç verece-
gini
biliyoruz. → bu yüzde
B) 6
x-11-(x-5)
(x+4)
eşitsizliğini kaç tam sayı değeri sağlar?
<0
almicaz-
x=4
C) 8
X=1
x=0
D) 9
n
5
+p+
1x
E) 7
(15=-31-²16/191/12)
304
ÇI
a
C
3
2)
(415)
→ bu yüzden on isaret tabulosue (3
katmanıza gerek.
x²-3x - a > 0
m

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri2.
3.
x²-5x-3=0 denkleminin kökleri x, ve x₂ dir.
²). (₁
Buna göre,
ğeri kaçtır?
A) 56
6x2 + x2
X₁
A) 6
B) 60
6X1 + X1
X2
C) 63
ifadesinin de-
D) 66
x²-3mx+8=0 denkleminin kökleri x, ve x₂ dir.
x₁=x²
olduğuna göre, x, +x₂ toplamı kaçtır?
B) 5
C) 4
E) 70
D) 3
6.
E) 2
E) X²-28-1=0
x²-3x-2-0 denkleminin kökleri x, ve x₂ dir.
Buna göre, kökleri x.x₂ ve x²+x² olan iki
receden denklem aşağıdakilerden hangisi
A) x²-26x+11=0
C) x²-11x-26=0
7.
B) x²+11x-26
D) x²-11x+2
E) x²+26x-11=0
Aşağıdaki y=f(x) fonksiyonunun go
![a<0<b olmak üzere,
x².(x + a)
(x + b) (ax² -b)
≤0
eşitsizliğinin gerçel sayılardaki çözüm kümesi aşa-
ğıdakilerden hangisidir?
A) (-b, 0]
B) (-∞0,-b) U[-a,∞o) U {0} C) [a, b) U {0}
D) [0, -a]
E) R - (0, -a)](https://media.kunduz.com/media/question/seo/raw/20230301220842055194-4822355.jpeg?w=256)
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleria<0<b olmak üzere,
x².(x + a)
(x + b) (ax² -b)
≤0
eşitsizliğinin gerçel sayılardaki çözüm kümesi aşa-
ğıdakilerden hangisidir?
A) (-b, 0]
B) (-∞0,-b) U[-a,∞o) U {0} C) [a, b) U {0}
D) [0, -a]
E) R - (0, -a)

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerit
B) 2 <m <3
x² + 4x + 4m-5
ifadesi -1 sayısından daima büyük olduğuna göre, m
aşağıdaki aralıklardan hangisinde bulunmaz?
A) m <2
D) 3 <m < 5
06-6₁-1+0<o
16+60 <s
x tuxt un
un c-36
475-9
C) 3<m<4
E) 3 < m

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik SistemleriORİJİNAL MAT
11. Aşağıdaki şekilde bir dikdörtgenler prizmasının santimet-
re cinsinden ayrıt uzunlukları verilmiş ve bazı yüzeyleri
sarı, mavi ve kırmızıyla boyanmıştır.
x>6 (x-6) br
-x718x-72
x <12
(x + 2) br
YAYINLARI
A) 17
2
2x-14x-360
x27x-18=2c
-9
12
2
X410X+24
X1. D
5. B
9.B =-2
x-9
NAL MATEMATİK
(12-x) br
Bu dikdörtgenler prizmasının kırmızıya boyalı yüzey ala-
ni K br², maviye boyalı yüzey alanı M br² ve sarıya boyalı
yüzey alanı S br² dir.
M>K>S
(x-6). (12-x)
eşitsizliği sağlandığına göre, bu dikdörtgenler priz-
masının farklı ayrıt uzunluklarının toplamının en kü-
çük tam sayı değeri kaç birimdir?
B) 18
C) 19
2. A
6. C
10. D
Cevap Anahtarı
12x-x²=72+bx
12/245-12
9-y
(12-x), (x+2)
+18x
x²=-ux-12 > _x² +10x+24)-72
D) 20
-12x+24-x²=2X
3. B
7. E
11. B
E) 21
6<x<9
78
4. C
8. A
495
163

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri30. 1, 3, 5, 7) ve (2, 4, 6, 8, 10) kümelerinden sırasıyla
a ve b gibi iki eleman seçilerek rasyonel sayısı oluş-
(90)=2
turuluyor.
Buna göre,
b
1 <
A)
a
1
2
<4
eşitsizliğini sağlama olasılığı kaçtır?
2
5
B)
9
20
b
a
C)
D)
7
20
E)
3
10
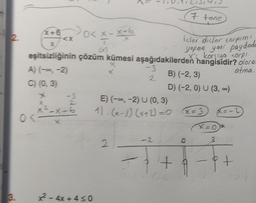
Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri3.
(x+0<x
<X
X
eşitsizliğinin
A) (-∞, -2)
C) (0, 3)
x²-x-6
0 <-
=332
O< x-x-6
T
isler dislor sarpımı
yapma yani poydode
çözüm kümesi aşağıdakilerden hangisidir? olora
X's korşıya sorp!
atma.
2-4x+4≤0
x
X
-3
2
E) (-∞, -2) U (0, 3)
1)-(x-3) (x+2) =2
-2
7 tone
B) (-2, 3)
D) (-2, 0) U (3, ∞)
+
x=3
(X=0
3
x=-2
i +

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemlerigi-
15.
Yukarıdaki şekilde 3 köy arasındaki yol haritaları ve-
rilmiştir.
--920
+3x+6
2
A köyü ve B köyü arasındaki yol, B. köyü ile C
köyü arasındaki yoldan uzun değildir.
B köyü ile C köyü arasındaki yol, A köyü ile C
arasındaki yoldan kısadır.
+
20 (3x²-
- 7x + 15) km,
BC yolu (2x2 + 3x + 6) km,
AC yolu (x²+
3241246
+ 3x + 15) km uzunluğundadır.
2,11
Buna göre, bu şartı sağlayan kaç farklı x doğal
sayısı vardır?
48-28+17
B) 2
C) 3
E) 5
3x²=7x+15 < 2x²+3x+b
x²-10x+920
-99
0/6+
D) 4
(1.9)
L

Lise Matematik
İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri20+1 ²
4-
600 12395000
80 Pino
240
480
il
Çanakkale
Hakkari
K.Maraş
Samsun
Yalova
Düzce
2/2
770
92
603
K.Maraş - Samsun
O Çanakkale - Hakkari
1360
110
060
D. Aşağıda bazı iller ve bu illere ait plaka kodları verilmiştir.
12
Plaka Kodu
17
30
46
55
77
81
360
110135
060
77
leketlerinin plaka kodları ile ilgili aşağıdakiler bilinmektedir.
Sertap ve Hülya'nın tabloda verilen illerden biri olan mem-
35 5
. İkisinin de memleketinin plaka kodunun iki asal çarpa-
nı vardır.
Hülya'nın memleketinin plaka kodunun asal çarpanla-
rının toplamı, Sertap'ın memleketinin plaka kodunun
asal çarpanlarının toplamından büyüktür.
E) Yalova - Düzce
Buna göre, Sertap ile Hülya'nın memleketi sırasıyla
şağıdakilerden hangisi olabilir?
B) Hakkari - K.Maraş
Samsun - Yalova
86 (A
32.
