Kosinüs Teoremi Soruları
![s(180-a)
cosa
12cosa
√12
B
A) 7
A
[BE] n [AD] = {C}
[AB] [AD]
2
of
Va
C
4
2
cos2
==12 pos
4
F
5
ne oblib b
8
olduğuna göre, x kaç cm'dir?
B) 6
C) 5
D
11X
x² = 25+64 +2.5.8. cosa
X
= 89+40=129
D) 8
E
E) 10](https://media.kunduz.com/media/question/seo/raw/20230222202635898258-663368.jpg?w=256)
Lise Matematik
Kosinüs Teoremis(180-a)
cosa
12cosa
√12
B
A) 7
A
[BE] n [AD] = {C}
[AB] [AD]
2
of
Va
C
4
2
cos2
==12 pos
4
F
5
ne oblib b
8
olduğuna göre, x kaç cm'dir?
B) 6
C) 5
D
11X
x² = 25+64 +2.5.8. cosa
X
= 89+40=129
D) 8
E
E) 10
![kaç
3
ABCD kare;
|FC| = |EB| = 2 br, |AD| = 6 br
olduğuna göre, cosa kaçtır?
COZUM
ÖRNEK SORU
3
●
4
ÇÖZÜM
D
10
6
E
[AE] n [BC] = {D}
[AB] [BC]
Şekilde verilenlere göre, x kaç br'dir?
O
X
Ave B bayrak
pan kuş Cr
stüne konm
JAE
olduğuna g
ALE O
A
E](https://media.kunduz.com/media/question/seo/raw/20230222190717080578-4512680.jpeg?w=256)
Lise Matematik
Kosinüs Teoremikaç
3
ABCD kare;
|FC| = |EB| = 2 br, |AD| = 6 br
olduğuna göre, cosa kaçtır?
COZUM
ÖRNEK SORU
3
●
4
ÇÖZÜM
D
10
6
E
[AE] n [BC] = {D}
[AB] [BC]
Şekilde verilenlere göre, x kaç br'dir?
O
X
Ave B bayrak
pan kuş Cr
stüne konm
JAE
olduğuna g
ALE O
A
E
Lise Matematik
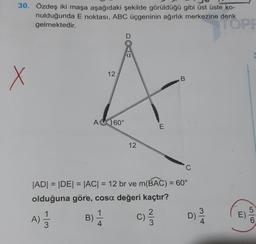
Kosinüs Teoremi30. Özdeş iki maşa aşağıdaki şekilde görüldüğü gibi üst üste ko-
nulduğunda E noktası, ABC üçgeninin ağırlık merkezine denk
gelmektedir.
x
12
A 60°
D
a
12
E
2
C) ²/3/3
B
|AD| = |DE| = |AC| = 12 br ve m(BAC) = 60°
olduğuna göre, cosa değeri kaçtır?
A) 1/12
B) 1/24
D) 3/14
TOPF
E)
56
![Analit
smm apsisi kaçtır?
A)
8)
(1)
9)
B
7
8
B) - 3
4
2
C)
(Q+b+c)(a+b-c) =
olduğuna göre cose kaçtır?
5
A) - 6
57
Bir ABC üçgeninde a, b, c üçgeninin kenarlarıdır.
a.b
2
Bo
D)
q.
Garpımlou- olmali.
E) - 2
C) - D)
2
C
2
2
-8X--X+10
-7x = 10
XHO
7
ABC bir diküçgen
[AB] L [AC]
[AD] L [BC]
m(ABC) = a
|AB| = 2 br
DC üçgeninin alanı aşağı-
b-cosu.
ifadesinin eşiti aşağıdakil
a
B)
A)
13)
D) b-a-
Yandaki şekilde
ABCD kare, [BD] köşege
|DE| = 7|EB|ve m(AED
olduğuna göre,
tan a kaçtır?
A)
3)
14)
Aşağıda y = f(x](https://media.kunduz.com/media/question/seo/raw/20230222153448690741-5105001.jpg?w=256)
Lise Matematik
Kosinüs TeoremiAnalit
smm apsisi kaçtır?
A)
8)
(1)
9)
B
7
8
B) - 3
4
2
C)
(Q+b+c)(a+b-c) =
olduğuna göre cose kaçtır?
5
A) - 6
57
Bir ABC üçgeninde a, b, c üçgeninin kenarlarıdır.
a.b
2
Bo
D)
q.
Garpımlou- olmali.
E) - 2
C) - D)
2
C
2
2
-8X--X+10
-7x = 10
XHO
7
ABC bir diküçgen
[AB] L [AC]
[AD] L [BC]
m(ABC) = a
|AB| = 2 br
DC üçgeninin alanı aşağı-
b-cosu.
ifadesinin eşiti aşağıdakil
a
B)
A)
13)
D) b-a-
Yandaki şekilde
ABCD kare, [BD] köşege
|DE| = 7|EB|ve m(AED
olduğuna göre,
tan a kaçtır?
A)
3)
14)
Aşağıda y = f(x
![B
A) √41
Jus
8
612
TYT-AYT/Geometri
O
A
C) 5√2
25+ 16 = x2
8
8√₂
D 2√2
00
61 = x²
ful = x
C
6√2
ABC ikizkenar üçgen, |AB| = |AC| = 8 cm
|DC| = 2√2 cm, [AB] [AC], D = [BC]
Yukarıda verilenlere göre, |AD| uzunluğu kaç cm dir?
A) 3√3
B) 5
64764
62128
C) 4√2
128p
6412
322
16 L
& 4222
D) 6
E) 6
E) 210
SORU BANKASI
A) 2√5
16.
B)
SORU BANKASI](https://media.kunduz.com/media/question/seo/raw/20230222112734033251-4567718.jpg?w=256)
Lise Matematik
Kosinüs TeoremiB
A) √41
Jus
8
612
TYT-AYT/Geometri
O
A
C) 5√2
25+ 16 = x2
8
8√₂
D 2√2
00
61 = x²
ful = x
C
6√2
ABC ikizkenar üçgen, |AB| = |AC| = 8 cm
|DC| = 2√2 cm, [AB] [AC], D = [BC]
Yukarıda verilenlere göre, |AD| uzunluğu kaç cm dir?
A) 3√3
B) 5
64764
62128
C) 4√2
128p
6412
322
16 L
& 4222
D) 6
E) 6
E) 210
SORU BANKASI
A) 2√5
16.
B)
SORU BANKASI

Lise Matematik
Kosinüs Teoremi6.
X
B
A
2
E
3
6
C
4
D
Yukarıdaki şekilde ABC ve ECD üçgen; B, C ve D doğru-
saldır. |BC| = 6 cm, |AE| = 2 cm
m(ECD) > 90°, |EC| = 3 cm, |CD| = 4 cm
|AB| = x cm, A(ECD) = 3√3 cm²
olduğuna göre, x değeri kaçtır?
A) √31
B) √79
C) √83
D) √85
E)√91

Lise Matematik
Kosinüs TeoremiTRIGONOMETRI - II
PLAM VE FARK FORMÜLLERİ
pos(a + b) = cosa cosb-sina sinb
os(a - b) = cosa cosb + sina sinb
EK-1
cos35° -
FI MATEMATİK
den
10.
6
A
10
B
ABC üçgeninde,
|AB| = 6 cm, |AC| = 10 cm, m(Â) > 90°
A(ABC) = 6√21 cm²
D) 5√43
ÖRNEK-4
olduğuna göre, BC kaç santimetredir?
A) 2√22
B) 2√46
E) 7√52
cos(>
C
C) 4√35
FOY UZ
DERY outery
cosa
Periyodik
for
sic
A
2.

Lise Matematik
Kosinüs Teoremi27. Aşağıdaki ölçeklendirilmiş haritada; A, B ve C nok-
talarının dik koordinat düzlemindeki koordinatları
verilmiştir.
A(2,8)
C(7, 20)
A) 11 B)
13
Buna göre, CAB açısının kosinüs değeri kaçtır?
D) 1/3
10
21
26
C)
B(10, 14)
56
65
E)
2
3/5
![2.
RIGONOMETRI VI (Toplam, Fark, Yarım Açı II)
m+n+x+y = 180
1.
Jx
B 2
tan xay
A
1-1
H
STO
3
2
Yukarıdaki verilere göre, m (BAC) kaç derecedir?
A) 45
B) 75
C) 105
D) 120
-ton(-x-y)
C
2+3
1-6
ABC bir üçgen
[AH] 1 [BC]
IAHI = 1 cm
IBHI = 2 cm
IHC| = 3 cm
3
34
E) 135](https://media.kunduz.com/media/question/seo/raw/20230221174931712483-758344.jpg?w=256)
Lise Matematik
Kosinüs Teoremi2.
RIGONOMETRI VI (Toplam, Fark, Yarım Açı II)
m+n+x+y = 180
1.
Jx
B 2
tan xay
A
1-1
H
STO
3
2
Yukarıdaki verilere göre, m (BAC) kaç derecedir?
A) 45
B) 75
C) 105
D) 120
-ton(-x-y)
C
2+3
1-6
ABC bir üçgen
[AH] 1 [BC]
IAHI = 1 cm
IBHI = 2 cm
IHC| = 3 cm
3
34
E) 135

Lise Matematik
Kosinüs TeoremiMETRI
Soru 80
birim
E5
TRIGONOMETRİ (KOSİNÜS - SİNÜS TE
1.
B
X
3
4 E 2 C
ABC bir üçgen
|AD| = 1 cm
|DC| = 3 cm
|CE| = 2 cm
|EB| = 4 cm
|AB| = 8 cm
|DE| = x
Yukarıdaki verilere göre, |DE| = x kaç cm dir?
A) 2√6
B) 2√5
C) 1772
D) 7
E) 4
![4.3
M İZLE O
XXD
9. Aşağıda verilen ABCD yamuğunda, [BD] açıortaydır.
B
TEST 10
55
A
a
√5
D) 5√3
X
m(A) + m(C) = 180°
olduğuna göre, |BC| = x değeri kaçtır?
A) 5
B) 6
D
E) 5√5
3
C) 5√2
11. Aşağıda A
r = 1
olduğur
A) 10](https://media.kunduz.com/media/question/seo/raw/20230221123745193633-1084750.jpg?w=256)
Lise Matematik
Kosinüs Teoremi4.3
M İZLE O
XXD
9. Aşağıda verilen ABCD yamuğunda, [BD] açıortaydır.
B
TEST 10
55
A
a
√5
D) 5√3
X
m(A) + m(C) = 180°
olduğuna göre, |BC| = x değeri kaçtır?
A) 5
B) 6
D
E) 5√5
3
C) 5√2
11. Aşağıda A
r = 1
olduğur
A) 10
![X = !
3.
+
x = 5
B
2 - sinx
D
(1 − sinx)
C
you is
0<x< olmak üzere,
hangisidir?
A) cosx
D) cotx
X = 20 +467
X = 217
S
ABC dik üçgen
[BD] [AC]
|AD|=2 sinx birim
|DC| = (1-sinx) birim
T
2
|BC| uzunluğunun x türünden eşiti aşağıdakilerden
B) 2cosx
xris
E) secx
C) tanx
0
6. E
YAYINLARI
d
ti
A
ORIJINAL MATEMATE](https://media.kunduz.com/media/question/seo/raw/20230220114949774964-5351263.jpg?w=256)
Lise Matematik
Kosinüs TeoremiX = !
3.
+
x = 5
B
2 - sinx
D
(1 − sinx)
C
you is
0<x< olmak üzere,
hangisidir?
A) cosx
D) cotx
X = 20 +467
X = 217
S
ABC dik üçgen
[BD] [AC]
|AD|=2 sinx birim
|DC| = (1-sinx) birim
T
2
|BC| uzunluğunun x türünden eşiti aşağıdakilerden
B) 2cosx
xris
E) secx
C) tanx
0
6. E
YAYINLARI
d
ti
A
ORIJINAL MATEMATE

Lise Matematik
Kosinüs Teoremi√5
x-1
14. Co
3m
NO
3 m
2 3 S 8
3
K 2m
a
D)
S
R
16
9√2
L
TNRS düzlemi NKMR düzlemine diktir. NKMR
karedir.
13
1m M
Şekildeki gibi gösterilen mancınık ile taş atan
Mete'nin konumu verilmiştir.
X Buna göre, cota değeri kaçtır?
A) 6√6
|TS| = 3 m
ITNE3m
|KL| = 2 m
|LM| = 1 m
|NK| = 3 m
m(TLS) = a
B)
9√2
4
E)
16
√√3
C)
3√2
4
![1.
Şekilde birim çember ve bu çember üz
n verilmiştir.
m(DCO) =a olduğuna göre,
23.
FASİKÜL
PEKİŞTİRME TESTİ
y = f(x) D
B
MA
C
f: [-4, -1] U [2, 5] → R olmak üzere bir tur şirketi müşterilerini
belirli bir şehrin f(x) = x² - 2x + m fonksiyonuna göre sırasıyla
A, B, C, D bölgelerine götürerek turu tamamlamaktadır. Gezi es-
nasında yanlışlıkla turdan ayrılan bir kişi kendi imkanlarıyla B
noktasından C ye, C noktasından D ye ve oradan da tekrar
ye doğrusal yollarla ulaşmayı başarmıştır.
B) 12
ÜNİT
Buna göre, bu kişinin B, C ve D noktası ile işaretlenmiş böl-
geleri gezdiği üçgensel bölgenin alanı kaç birimkaredir?
A) 9
C) 18
D) 27
|AB|
old
cin
2. M
n
E) 36](https://media.kunduz.com/media/question/seo/raw/20230218115726044372-5007667.jpeg?w=256)
Lise Matematik
Kosinüs Teoremi1.
Şekilde birim çember ve bu çember üz
n verilmiştir.
m(DCO) =a olduğuna göre,
23.
FASİKÜL
PEKİŞTİRME TESTİ
y = f(x) D
B
MA
C
f: [-4, -1] U [2, 5] → R olmak üzere bir tur şirketi müşterilerini
belirli bir şehrin f(x) = x² - 2x + m fonksiyonuna göre sırasıyla
A, B, C, D bölgelerine götürerek turu tamamlamaktadır. Gezi es-
nasında yanlışlıkla turdan ayrılan bir kişi kendi imkanlarıyla B
noktasından C ye, C noktasından D ye ve oradan da tekrar
ye doğrusal yollarla ulaşmayı başarmıştır.
B) 12
ÜNİT
Buna göre, bu kişinin B, C ve D noktası ile işaretlenmiş böl-
geleri gezdiği üçgensel bölgenin alanı kaç birimkaredir?
A) 9
C) 18
D) 27
|AB|
old
cin
2. M
n
E) 36

Lise Matematik
Kosinüs Teoremi6
B
Geometrik Sekillerde
Trigonometrik Oranlar
ORTA SEVİYE
8
12
C
Şekildeki ABC üçgeninde, |AB| = 6 cm,
|AC| = 12 cm, |BC| = 8 cm
olduğuna göre, 6 cos à +8 cos C
sinin değeri kaçtır?
A) 12
B) 10
C) 9
ifade-
D) 6 E) 5
K
BI
Trig
Ve
sin
ri

Lise Matematik
Kosinüs Teoremi2
5. Bir ABC üçgeninin kenar uzunlukları a cm, b cm ve c cm
olmak üzere, kenar uzunlukları arasında kosinüs teore-
mine göre,
a²=b²+ c²-2b-c-cosÃ
bağıntısı vardır.
A) 30
b-a=
c(b-c)
a+b
olduğuna göre, a kenarının karşısındaki açı kaç
derecedir?
B) 45
C) 60
P
D) 75
E) 90
