Limit Özellikleri Soruları
![168
-2 -1
1
0
1
-1
-2
-3
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lim
(1) =
A
X
*+(9)*
X-
lim
B
X
olduğuna göre, B+ A toplamı kaçtır?
A)-2
B)-1
C) 0
D) 2
E) 3
3D YAYINLAI](https://media.kunduz.com/media/question/seo/raw/20220603181023352082-3798883.jpg?w=256)
Lise Matematik
Limit Özellikleri168
-2 -1
1
0
1
-1
-2
-3
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lim
(1) =
A
X
*+(9)*
X-
lim
B
X
olduğuna göre, B+ A toplamı kaçtır?
A)-2
B)-1
C) 0
D) 2
E) 3
3D YAYINLAI
![AY
4
3
1
- 1
3
X
4-3
0
1
:2
-1
1-2
-3
4
Yukarıda f: (-4, 3) (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lim
f
12
1
X
= A
+
X
lim
f
©
-B
x-(-3)
olduğuna göre, B+ A toplamı kaçtır?
A) 2
B)-1
C)
D) 2
E) 3](https://media.kunduz.com/media/question/seo/raw/20220314225123912326-4133472.jpg?w=256)
Lise Matematik
Limit ÖzellikleriAY
4
3
1
- 1
3
X
4-3
0
1
:2
-1
1-2
-3
4
Yukarıda f: (-4, 3) (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lim
f
12
1
X
= A
+
X
lim
f
©
-B
x-(-3)
olduğuna göre, B+ A toplamı kaçtır?
A) 2
B)-1
C)
D) 2
E) 3
![186
9.
●
-4-3
A)-2
lim
(2016
-2 -1
lim
4
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lo
f(1) = B
-2
3
0
-2
-3
1
A=1
2
-2
FO
To
olduğuna göre, B + A toplamı kaçtır?
B)-1
C) 0
3
➤X
4-3=15
D) 2
1152
E) 3
YAYINL](https://media.kunduz.com/media/question/seo/raw/20230125190520291272-3080314.jpeg?w=256)
Lise Matematik
Limit Özellikleri186
9.
●
-4-3
A)-2
lim
(2016
-2 -1
lim
4
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
lo
f(1) = B
-2
3
0
-2
-3
1
A=1
2
-2
FO
To
olduğuna göre, B + A toplamı kaçtır?
B)-1
C) 0
3
➤X
4-3=15
D) 2
1152
E) 3
YAYINL
![X-220 (x) = log5 (x-2) fonksiyonunun süreksiz olduğu
x≤2
en geniş aralık (-∞, 2] dir.
ifadelerinden hangileri doğrudur?
B) Yalnız II
+0₁1
6
9.
A) Yalnız I
A)-2
K dir.
D) II ve III
lim
-4-3
lim f
-2 -1
B
B
(9)-
3
=B
0
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
(¹) - A
=
X
-1
-2
-3
1
E) I, II ve III
olduğuna göre, B+ A toplamı kaçtır?
B)-1
C) 0
N
3
D) 2
C) I ve II
E) 3
3D YAYINLARI
12.](https://media.kunduz.com/media/question/seo/raw/20221219113116773358-4370139.jpg?w=256)
Lise Matematik
Limit ÖzellikleriX-220 (x) = log5 (x-2) fonksiyonunun süreksiz olduğu
x≤2
en geniş aralık (-∞, 2] dir.
ifadelerinden hangileri doğrudur?
B) Yalnız II
+0₁1
6
9.
A) Yalnız I
A)-2
K dir.
D) II ve III
lim
-4-3
lim f
-2 -1
B
B
(9)-
3
=B
0
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
(¹) - A
=
X
-1
-2
-3
1
E) I, II ve III
olduğuna göre, B+ A toplamı kaçtır?
B)-1
C) 0
N
3
D) 2
C) I ve II
E) 3
3D YAYINLARI
12.
![9.
lim
1
2
A)-2
-4-3
X-→
-2 -1
T
M
lim
1
*+(-3)
X→
4
3
1
0
AY
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
(1) = A - 2
-1
-2
-3
-4
1
f(1) = B
500(0
olduğuna göre, B + A toplamı kaçtır?
B)-1
C) 0
"
2
3
D) 2
I
X
E) 3](https://media.kunduz.com/media/question/seo/raw/20221215121734247536-277811.jpg?w=256)
Lise Matematik
Limit Özellikleri9.
lim
1
2
A)-2
-4-3
X-→
-2 -1
T
M
lim
1
*+(-3)
X→
4
3
1
0
AY
Yukarıda f: (-4, 3] → (-4, 4], y = f(x)
fonksiyonunun grafiği verilmiştir.
(1) = A - 2
-1
-2
-3
-4
1
f(1) = B
500(0
olduğuna göre, B + A toplamı kaçtır?
B)-1
C) 0
"
2
3
D) 2
I
X
E) 3
Lise Matematik
Limit ÖzellikleriE) 12
2
230
B
L
12 2
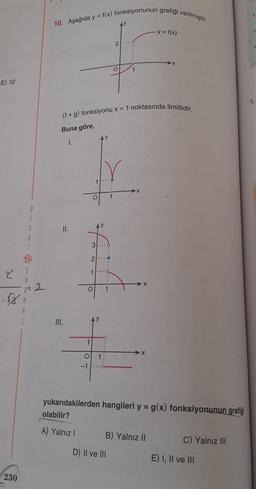
10. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
II.
III.
1
(f+g) fonksiyonu x = 1 noktasında limitlidir.
Buna göre,
1.
O
-1
O 1
3
2
1
AY
AY
1
1
2
O
1
D) II ve III
X
- y = f(x)
yukarıdakilerden hangileri y = g(x) fonksiyonunun grafiği
olabilir?
A) Yalnız I
B) Yalnız II
C) Yalnız III
E) I, II ve III
1.

Lise Matematik
Limit Özellikleri4. Gerçek sayılar kümesi üzerinde
f(x) =
(x-3)(x+2)
-, x#3 isex-
[x²-x-6
x-3
a
x = 3 ise
biçiminde tanımlanan f fonksiyonu tanım kümesi
üzerinde süreklidir
Buna göre, a kaçtır?
A) O
B) 1
C) 3
D) 5 E) 9
1.

Lise Matematik
Limit ÖzellikleriE) 12
2
230
B
L
12 2
10. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
II.
III.
1
(f+g) fonksiyonu x = 1 noktasında limitlidir.
Buna göre,
1.
O
-1
O 1
3
2
1
AY
AY
1
1
2
O
1
D) II ve III
X
- y = f(x)
yukarıdakilerden hangileri y = g(x) fonksiyonunun grafiği
olabilir?
A) Yalnız I
B) Yalnız II
C) Yalnız III
E) I, II ve III
1.
![Mutlak Değer ve Parçalı Fonksiyonların Limiti
1. y=f(x) fonksiyonunun grafiği şekildeki gibidir.
en
3
Buna göre, lim
x-a
f(x)
|f(x)\
limitinin varolabilmesi
- Ohomali
için a gerçel sayılarının değer kümesi aşağıda-
kilerden hangisidir?
A) 2
y = f(x)
C)R--6-2,3,5}
➤X
B) (-6, -2) U (3,5)
D) R-{-6, -2, 1, 3, 5}
5:00p.m
E) -6, -2]U[3, 5]U (1)
AV
VI
2. y=f(x) fonksiyonunun grafiği şekildeki gibidir.
- y = f(x)
lim
limitin
A) Yo
5.](https://media.kunduz.com/media/question/seo/raw/20230207124655053939-910366.jpeg?w=256)
Lise Matematik
Limit ÖzellikleriMutlak Değer ve Parçalı Fonksiyonların Limiti
1. y=f(x) fonksiyonunun grafiği şekildeki gibidir.
en
3
Buna göre, lim
x-a
f(x)
|f(x)\
limitinin varolabilmesi
- Ohomali
için a gerçel sayılarının değer kümesi aşağıda-
kilerden hangisidir?
A) 2
y = f(x)
C)R--6-2,3,5}
➤X
B) (-6, -2) U (3,5)
D) R-{-6, -2, 1, 3, 5}
5:00p.m
E) -6, -2]U[3, 5]U (1)
AV
VI
2. y=f(x) fonksiyonunun grafiği şekildeki gibidir.
- y = f(x)
lim
limitin
A) Yo
5.
![re: 25 dk
aka izle.
-).(3ax 2).
16
hayalkurun.com
3 U
-12
= 2
E) 12
9=2x3
-2x3
5.
ÖDEV TESTİ 13
x².(x²-1). (x³+1)
x²+1
olduğuna göre, f'(1) kaçtır?
f(x) =
122
A) 1
B)
x = (x + 1)²(x ² + 1)
(x²+1)
2 f'(x) = [2²(x-TT + []₁1
6. f:R* →R tanımlı bir fonksiyon olmak üzere,
f(x) = x³-3x²
fonksiyonu veriliyor.
C) 1
97899
D) 2
E) 4
C](https://media.kunduz.com/media/question/seo/raw/20230207101916256697-4130124.jpg?w=256)
Lise Matematik
Limit Özelliklerire: 25 dk
aka izle.
-).(3ax 2).
16
hayalkurun.com
3 U
-12
= 2
E) 12
9=2x3
-2x3
5.
ÖDEV TESTİ 13
x².(x²-1). (x³+1)
x²+1
olduğuna göre, f'(1) kaçtır?
f(x) =
122
A) 1
B)
x = (x + 1)²(x ² + 1)
(x²+1)
2 f'(x) = [2²(x-TT + []₁1
6. f:R* →R tanımlı bir fonksiyon olmak üzere,
f(x) = x³-3x²
fonksiyonu veriliyor.
C) 1
97899
D) 2
E) 4
C

Lise Matematik
Limit ÖzellikleriT@stokul
5. a ve b gerçel sayılar olmak üzere,
3x² + ax - 1
x³ - 1
lim
X-1
B
3
= b
eşitliği veriliyor.
Buna göre, a b çarpımı kaçtır?
-8
A) -33
3+0-1
-
-5
3
3+0-1
(
D)-2
(3x+1)(x-1)
(x-1). (X+X+1)
E) -1
![SÜREKLİLİK
96.
ay-
ha-
a-
APOTEMI
O halde, f'in, tanımlı olduğu en geniş aralık (-00, 1] aralığı-
dır. f fonksiyonu, en geniş tanım kümesi olan (-00, 1] ara-
lığında her x için süreklidir.
●
●
.
DİKKAT!
f(x) en geniş tanım kümesinde sürekli bir fonksiyon ise
► f(x) |
► √f(x)
► log(f(x))
► af(x)
şeklindeki fonksiyonlar en geniş tanım kümelerinde yer
alan her x gerçel sayısı için sürekildir.
Polinom fonksiyonlar gerçel sayılar kümesinde sürek-
lidir.
Sürekli bir fonksiyonun, tersi de fonksiyon ise tersi olan
fonksiyon da süreklidir.
ÖRNEK (10)
Bu kısmın mantığını açıklayabilir misiniz?](https://media.kunduz.com/media/question/seo/raw/20230207060431716175-2616087.jpeg?w=256)
Lise Matematik
Limit ÖzellikleriSÜREKLİLİK
96.
ay-
ha-
a-
APOTEMI
O halde, f'in, tanımlı olduğu en geniş aralık (-00, 1] aralığı-
dır. f fonksiyonu, en geniş tanım kümesi olan (-00, 1] ara-
lığında her x için süreklidir.
●
●
.
DİKKAT!
f(x) en geniş tanım kümesinde sürekli bir fonksiyon ise
► f(x) |
► √f(x)
► log(f(x))
► af(x)
şeklindeki fonksiyonlar en geniş tanım kümelerinde yer
alan her x gerçel sayısı için sürekildir.
Polinom fonksiyonlar gerçel sayılar kümesinde sürek-
lidir.
Sürekli bir fonksiyonun, tersi de fonksiyon ise tersi olan
fonksiyon da süreklidir.
ÖRNEK (10)
Bu kısmın mantığını açıklayabilir misiniz?

Lise Matematik
Limit Özellikleri13. Aşağıdaki şekillerde y = f(x) ve y = g(x) fonksiyonlarının gra-
fiklerinin birer bölümleri verilmiştir.
y = f(x)
-3
-2
L
4
2
X-2
-2
lim g(x)
gift
AY
3
f(x) tek fonksiyon ve g(x) çift fonksiyon olduğuna göre,
3
lim f(x)
lim f(x))+ lim g(x)
x-3
X -2
6
2
w/5
y = g(x)
ifadesinin değeri kaçtır?
3
3
A)
E)
-2 B) 3 C) -1 D) - E2
4
4

Lise Matematik
Limit ÖzellikleriASF 20
6. Gerçel sayılarda tanımlı f fonksiyonu için,
lim f(x)=3
X-2*
A)
olduğuna göre, lim f(x+1)+2f(3-x) limitinin değeri
kaçtır?
X-1*
2x + f(2*)
5
B)
lim f(x) = 1
X->2
5
242h
C) 1
ANALİZ TESTİ
4
34
9.
Birim
fonk
Lise Matematik
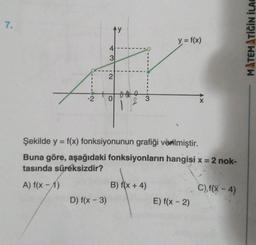
Limit Özellikleri7.
4
D) f(x-3)
3
2
0
00
y = f(x)
Şekilde y = f(x) fonksiyonunun grafiği verilmiştir.
Buna göre, aşağıdaki fonksiyonların hangisi x = 2 nok-
tasında süreksizdir?
A) f(x-1)
B) f(x + 4)
X
E) f(x - 2)
C), f(x-4)
MATEMATİĞİN İLAC

Lise Matematik
Limit Özelliklerilim
X-a
A)
Yukarıda y = f(x) fonksiyonunun grafiği verilmiştir.
f(x)
f(x-a)
olduğuna göre,
4a
lim
x-b
a
12(x)-f(x)-a (a-1)
1²(x) - a²
limitinin değeri aşağıdakilerden hangisine eşittir?
=4
D) 1-.
a
1
2a
b
B)
2a
E) 1+-
2a
C) 1
