Limit Özellikleri Soruları

Lise Matematik
Limit Özellikleri26.
a ve b birer gerçek sayı olmak üzere,
x³+a, x< 1 ise
f(x) =
ax:b, x≥lise
biçiminde tanımlanan f fonksiyonu gerçek sayılar
kümesi üzerinde türevlidir.
Buna göre, a-b farkı kaçtır?
A) -3
B) -1
c) 0
D) 2
E) 4
3-1
6
at
29.

Lise Matematik
Limit Özellikleriendemik
In
O
5. f(x) üçüncü dereceden başkatsayısı 1 olan bir polinom
fonksiyondur.
VxER için f(-x) = -f(x) -
f(1) = -3
olduğuna göre
f(x)
lim
X-2 X-2
ifadesinin değeri kaçtır?
A) 2
B) 4
C) 6 D) 8 E) 9
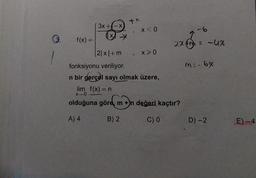
Lise Matematik
Limit Özellikleri€3.
f(x) =
3x +-X
X
*
+x
x < 0
9
|2|x|+ m
fonksiyonu veriliyor.
n bir gerçel sayı olmak üzere,
lim f(x) = n
X-0
olduğuna göre, m +n değeri kaçtır?
A) 4
B) 2
C) 0
X>0
-6
2x3 =
2x = -4x
m=-6x
D) -2
E) -4
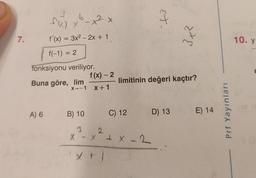
Lise Matematik
Limit Özellikleri7.
1
6
fxx) x²-x²
f'(x) = 3x² - 2x + 1
f(-1) = 2
fonksiyonu veriliyor.
Buna göre, lim
X→-1
A) 6 B) 10
3
2 x
f(x) - 2
X+1
st.
limitinin değeri kaçtır?
C) 12 D) 13
2
X-XX-2
X + j
3x²
E) 14
Prf Yayınları
10. y

Lise Matematik
Limit Özelliklerif(x) =
-
A) 2
x-3
x²-14
2x+1
B) 3
4x-1
x-10
3, 5, 10
4
2-D
1
*
fonksiyonunun gerçek sayılarda süreksiz olduğu kaç
farklı x değeri vardır?
X≤3
3<x<5
x ≥5
C) 4
x²-14:
3-D
4-C
P) 5
5-D
6-B
E) 6
14. Gerçek sayılarda f fonksiyonu a
yor.
7-C
X
f(x)==-=-1x1
Buna göre, aşağıdaki ifade
A) ffonksiyonu x=-2 apsisl
B) f fonksiyonu x=-2 ap
C) f fonksiyonunun sürel
8-D
D) f fonksiyonu x=
süreksizdir.
Ef fonksiyonunun sü
9-D
www
1
10-C 11-C

Lise Matematik
Limit ÖzellikleriGerçel sayılar kümesi üzerinde tanımlı f fonksiyonunun
grafiği aşağıdaki dik koordinat düzleminde verilmiştir.
1
3
lim g(x) - lim g(x)
*→0*
X40
A) 6
f + g fonksiyonu x = 0 noktasında sürekli olduğu-
na göre,
ifadesinin değeri kaçtır?
B) 5
y = f(x)
C) 2
X
D) - 2
E) - 4
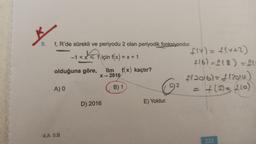
Lise Matematik
Limit Özellikleri5.
f, R'de sürekli ve periyodu 2 olan periyodik fonksiyondur.
-1 < x < 1 için f(x) = x + 1
olduğuna göre, lim f(x) kaçtır?
X→ 2016
B) 1
A) 0
4.A 5.B
D) 2016
C
E) Yoktur.
2
f(x) = f(x+2)
+16)=L(8) = fu
f(2016) = (2014)
= + (2)=(26)
233

Lise Matematik
Limit ÖzellikleriA) 1
18 cm
529
8. Aşağıda bir kenar uzunluğu 18 cm olan kare şeklinde-
ki bir karton verilmiştir.
B) 2
lim V(x)
x-3
X
Şekil 1
Rehber Matematik
D) 4
Bu kartonun köşelerinden bir kenarı x br olan boyalı
kareler kesilip çıkartılıyor. Kalan şekil kesikli yerlerden
katlanarak şekil 2'deki kutu elde ediliyor.
Kutunun hacmi V(x) olmak üzere,
C) 144
Şekil 2
2
4x²
288 96 324-4x
27
ifadesinin değeri kaçtır?
3
A) 96
B) 120
D) 156
E) 5
=96
2 38/4
278
E) 180
147
REHBER
MATE

Lise Matematik
Limit ÖzellikleriALAN YETERLİLİK TESTİ
X> 2
(x+3
f(x) = 2x-m, x ≤2
25.
fonksiyonu x = 2 noktasında sürekli olduğuna göre,
m kaçtır?
G
A)-9
2+325
21
BKT
572
2-2-M
4-1922
25m
122
lim
X->X X-XO
4-
D) 3
26. f fonksiyonunun türevi f' olmak üzere,
f(x)-f(x) = f'(x) dir.
Matematik
E) 9
11
Friend
USTKT
27. Ge
DER
K
i
* 28.
XXX
A
ole
y
if:
A

Lise Matematik
Limit Özellikleri14.
limitinin değeri kaçtır?
C) 1/3
D) /
x--6√√x+++x-6√x+²+
Jim
x-8
√x+1-3
X-8
A) 1 B) /
2/3
2
8)
fonksiyonu her reel sap in straks de
b kaç olmalidir?
A)-8
3.
8)-6
f(x)=-a.
şeklinde tanımlanan f
rekli olması için kaç
A) 1
B) 2

Lise Matematik
Limit ÖzellikleriO
f(x) =
g(x) = -
2 + x x < 2
x ≥ 2
x + 3
A)-2
f
I
x < -2
2x+1, x ≥-2
fonksiyonları veriliyor.
LG G5
lim (fog)(x)
x-a
B)-1
limiti olmadığına göre, a nın alabileceği değerle-
rin çarpımı kaçtır?
C) 1
D)=1/1/2
E) 2

Lise Matematik
Limit Özellikleri2. Uygun koşullarda tanımlı bir f fonksiyonu
f(x) = x²+2x+1 + x² + x² - 2x+1
3x+3
2x
x-1
olarak tanımlanıyor.
Buna göre,
lim f(x) + limf(x) + limf(x)
ifadesinin değeri kaçtır?
C) - D) - E) -1
3
A)-2 B) 5 C)-2D) -

Lise Matematik
Limit Özelliklerialın
?
lim
X-2+
lim
x-2+
|x2 − 5x+6
|x-4|-|x|
limitinin sonucunu bulunuz.
x → 2+ için
x → 2+ için
x → 2+ için
ÇÖZÜM
Mutlak değerli ifadelerin işaretlerini, inceleyelim.
x2 − 5X + 6 = (X − 2)(x − 3)
X
2
3
+
-(x-2)(x-3)
-(x-4) - X
ÖRNEK
x2 – 5X + 6 < 0
X-4 <0
X>0
= lim
=
X-2+
lim
X-2+
+
-(x-2)(x-3)
-2(x-2)
x-3
2
-1
= bulunur.
2
![sayısı
iz III
APOIEMI
lim f(x) = c
x→a
A) 2.b
olduğuna göre,
lim
f(x) → c
limitinin değeri aşağıdakilerden hangisine eşittir?
-4
Buna göre,
A)-5
[(x-1)-1(x)]
D) a-b-b
a
B) 2.a
(C-1). a
2
B)-3
8. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
AY
lim [f(x - 1x) + f(x)] = a
x→a
O 1
Xemio A
E) 2.b-2
C) 1
(8
LO
5
S(A
C) a.b
f
9100 nupublo
eşitliğini sağlayan a değerlerinin toplamı kaçtır?
D) 3
(A
X
E) 5](https://media.kunduz.com/media/question/seo/raw/20221231075703059350-4839923.jpeg?w=256)
Lise Matematik
Limit Özelliklerisayısı
iz III
APOIEMI
lim f(x) = c
x→a
A) 2.b
olduğuna göre,
lim
f(x) → c
limitinin değeri aşağıdakilerden hangisine eşittir?
-4
Buna göre,
A)-5
[(x-1)-1(x)]
D) a-b-b
a
B) 2.a
(C-1). a
2
B)-3
8. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir.
AY
lim [f(x - 1x) + f(x)] = a
x→a
O 1
Xemio A
E) 2.b-2
C) 1
(8
LO
5
S(A
C) a.b
f
9100 nupublo
eşitliğini sağlayan a değerlerinin toplamı kaçtır?
D) 3
(A
X
E) 5

Lise Matematik
Limit Özelliklerix = a gerçel sayısı için sürekli olan bir f fonksiyonu,
[g (x) , x≤ a
"
h(x) x>a
f(x) =
biçiminde tanımlıdır.
Buna göre;
AXYall
lim g(x)= lim h(x)
x→a
x → a
"
Yalnız I
g(a) = h(a)
III. g(a) = lim_h(x)
x→a+
ifadelerinden hangileri kesinlikle doğrudur?
D) I ve III
at h(x)
a--
B) Yalnız III
g(x)
g(x) =h(x)
Gi
€) 1₁
I, II ve III
I ve III

Lise Matematik
Limit Özellikleri11
2
15.
mx²-3x + 2
f(x) =
{
nx - 3
=6+C
X≤ 1
X > 1
fonksiyonu x = 1 apsisli noktasında türevli olduğuna göre,
m.n çarpımının değeri kaçtır?
A) 25
B) 30
C) 35
^-x=M-X12
1-M=2
D) 40
E) 45
MX-1=1
A-M-1=A
