Limit ve Süreklilik Soruları

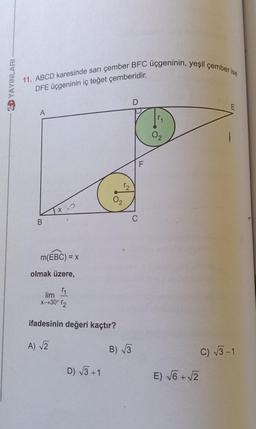
11. ABCD karesinde sarı çember BFC üçgeninin, yeşil çember ise D YAYINLARI DFE üçgeninin iç teğet çemberidir. D E A F x-2 C B m(EBC) = x olmak üzere, lim 11 *-+30° r2 ifadesinin değeri kaçtır? A Z B) V3 C) 73-1 D) 73 +1 E) V6 +2 +

. YAYINLAT Buna göre, lim m(EAD) limitinin değeri kach D C A) 30 B) 45 C) 60 ORESTSAL D) 75 G ton attab tomartonb torilor) 6. Bir ABC üçgeninde AB kenarının BC kenarı üzerinde dik izdüşümü 12 birim, AC kenarının yine BC kenan rindeki dik izdüşümü 25 birimdir. A a e Qa 8. G tong = th tono, t 25 tono B. 12 H 25 C Şekilde verilenlere göre, lim IACT limitinin değei 0-2a kaçtır? A) 65 B) 58 C) 48 D) 34 E) 25

(och lim TABI a 0 DCI limitinin değeri kaçtır? A) O 1 B) C) 2 Sind ford 13 E) 2 ORIJINAL MAT 10. Aşağıda (*) aralığında tanımlı f(x) = tan2x fonksiyo- nunun grafiği verilmiştir. fml=form to2mamm team M(m,f(m)) P mr flm) - 3. y = tan2x lir. Yukarıda x eksenine teğet olan çemberin merkezi olan M noktası f(x) = tan2x fonksiyonunun üzerinde hareket etmektedir. Buna göre, lim |OM|+|OT] limitinin değeri kaçtır? m0* IMTI A) 2 √5-1 B) C) 3 D) V5-1 2 2 Cevap Anahtarı 2.C 3.C 7.D 8.B √2+1 5+1 E) 2 1.D 4.E 5.E 9.D 6.B 10.E JİNALY MATEMATİK All in YAYINLARI

18. Gerçek sayılar kümesi üzerinde tanımlı ve sürekli y = f(x) fonksiyonunun grafiği Oy eksenine göre, y = g(x) fonksiyonunun grafiği ise orijine göre simetriktir. lim (f(x) +g(x)) = 12 ec fonk, x2+ lim_ (f(x) + g(x)) = 4 x-2 X-2 X2 olduğuna göre, lim f(x)• lim g(x) çarpımının değeri kaçtır? D) 24 E) 32 C) -16 B)-24 A) 2 16 DI -

pery 5(2) (1) gloor Plo) 941) ? 2 -1 0 1 2 o 1 3 y=81x) yfx -3 Yukanda y = f(x) ve y = g(x) fonksiyonlarının grafikleri verilmiştir. if Xx) fonksiyonun süreksiz olduğu x değerlerinden biri Be asagidakilerden hangisidir? A1 has no b D) 2 13 To = O=0 F

Orta TEST Orta-Zor Kolay Orta Kolay Zor 3 1x1 X = 11. 1. f(x) = II. fz(x) = |x – 21 III. f3(x) = ||x + 11 + 11 IV. f4(x) = x/x – 31 Verilen fonksiyonlardan kaç tanesi (-00,00) aralığında süreklidir? A) 1 B) O C)2 D) 4 E) 3

Türen - Gats=2 40=-3 2 f(x) limiti > 4) tanim 2 2) dimitli 3) Himiti = tanimi 20) Di=-3 2ax + 5, x<2 G f(x) = {x+ 2 X= 2 26-3=2 bx - 3,X> 2 26=5 b=5 2 fonksiyonu x = 2 noktasında sürekli ise a.b kaçtır? & sorg lim=sol limit 7 7 7 7 A) B) B) - C) O D) E) 4 8 8 4 La +5 = 26-3= 2 A4 fonk 21) 5.-3. -15 go ilo ise a 2 X-3 f(x)=

çember yalnız ikisinin hem çembere hem de yamuga ait olma A, B, C, D, E, F, G, H noktalarından seçilen üç noktadan olasılığı kaçtır? 2 B) A 4) bir H Z H R E N K 16. Gerçel sayılar kümesinde tanımlı f fonksiyonu her x gerçel sayısı için, 2 s f(x) = 6 2COCHLSC6 eşitsizliği sağlanıyor. Buna göre, f(x) 1. lim vardır. > Ş=- X-5 X X5 II. lim x.f(x) vardır. U III. lim (/f(x)]- f(x)) vardit. X-5 ifadelerinden hangileri daima doğrudur? A) Yalnız! B) Yalnız Il Yalnız III of D) Il ve II /1, II ve III

28-) 1991 OYS nelemanlı bir kümenin r-li bütün kombinasyon- larının (kombinezonlarının) sayısı C(n,r) ile gös. terildiğine göre, C(n. 1)C(n.4) lim C(n. 2)C(n.3) değeri kaçtır? D) 1 E) 2 A) B); c C) 1 / 1 ) 3

3. Gerçek sayılarda tanımlı f(x) fonksiyonu için lim f(x)= 4 X-2 4 olduğuna göre, 1. lim f(x) = 4 tür. x-2+ II. lim f(x) = 4 tür. X-2 III. f(2) = 4 tür. = ifadelerinden hangileri daima doğrudur? A) Yalnız ! B) Yalnız II C) Yalnız III E) I, II ve III D) I ve II

SÜRE 5. a ve b birer pozitif gerçel sayı olmak üzere, gerçel sa- yılar kümesi üzerinde sürekli olan bir f fonksiyonu (x² +n X<a f(x) = = 4 a<x<b X + 1 X> b biçiminde tanımlanıyor. f(a+b) = 6 olduğuna göre, n kaçtır? A-3 B) - 2 C) -1 D) O E) 1 6+1=4 b=3 ohan = 4

2 x2 - mx+1, x>-1 ise (mx-2) 2 -2m-3, X<-1 ise 5. f(x) ol ke biçiminde tanımlı y = f(x) fonksiyonunun yalnız bir nok- tada limiti yoktur. A Buna göre, m nin alamayacağı değerlerin çarpımı Prf Yayınları 6 kaçtır? lin X- A) 3 B) 2 C) 1 D) -1 E) -2

Xl1xH) cs 179) değeri asagidakilerden hangisidir? g(1) ta = A) 2 C Dj 15. g(x) bir fonksiyondur. x+ g(x) x< 1 ise f(x) = b ; X = 1 ise xg(x)+a , x> 1 ise 911 3. na göre, a nin ? fonksiyonu x = 1 de sürekli olduğuna göre, gia f(x) = x2 + 12 fonksiyonu içi 412+1)-912) lim aşağıdakilerden hangisidir? E) 5 b degeri aşağıdakilerden b B) 2 1 A) C) b + 1 2. A) B) C o 2 Db E) b-1 ch tar

18. f fonksiyonu tanımlı olduğu aralıkta türevlenebilen bir fonksiyon olmak üzere, f(x) = 6. x + 6 biçiminde veriliyor. f(x) - (2) Buna göre, lim limitinin değeri kaçtır? x² - 4 2 X-2 A) 27 B) 21 C) 18 E) 3 D) 6

- == 8 eşitliği veriliyor. X-2 X2 - 6. y = f(x) fonksiyonu için lim f(x) - 3 X2 X - 4 f(x) + 3x -9 Buna göre lim x2 X-2 A) 30 B) 32 C) 35 değeri kaçtır? = 3 Ölçme, Değerlendirme ve Sinav Hiz D) 40 E) 48 7. AY y=f(x) 74

sin (ax) bx lim X -- 0 a . cosx-sin Coszto olmaktadır. B 1 Dik koordinat düz- leminde Omer- kezli birim çeyrek çember yayı gra- fikte gösterilmiştir. m(COD)= a [CD]1[AO] A(ADC) = 5 X Buna göre, S lim ifadesinin değeri kaçtır? A) 1 1 / 2 B) B C) 1 D) 2 E) 4