Logaritmanın Kuralları Soruları

13. Aslan Öğretmen, sınıfına aşağıdaki konuşmayı yapıyor: - Her öğrenci sıfırdan ve birden farklı iki rakam seçip rakamların birini logaritma tabanı, diğerini logaritma üssü olarak kullanarak log b biçiminde logaritmik ifadeler elde edecek ancak logaritmik ifadenin sonucu 1 olmayacak. Sınıftaki öğrencilerden Ahmet, Berk ve Cüneyt'in elde ettiği ifadeler ile ilgili olarak D Ahmet'in elde ettiği ifadenin, Berk'in elde ettiği ifadeye oranı log₂3'tür. ● Berk'in elde ettiği ifadenin, Cüneyt'in elde ettiği ifadeye oranı log54'tür. bilgileri veriliyor. Buna göre, bu üç öğrencinin seçtiği rakamlar ile oluşturulan kümenin elemanları toplamı aşağıdakilerden hangisi olabilir? A) 30 B) 29 C) 28 D) 27 E) 26

ER DENEME-9 ²717x²4 log(x2 + x4x² = n los olduğuna göre, log (1 x ² [x²41) x (1+x2)(x² + x²) 0000 ifadesinin n türünden eşiti aşağıdakilerden hangisidir? 1 A) J₁ B) C) 1-n D) n-1 1-n n-1 E) n + 1 X 10917x²2 +110. 20 ²x²= 7+. X+X hi?

6. Matematik dersinde, Görkem sırasıyla aşağıdaki adımları takip ederek işlemler yapmıştır. 1. adım: 18 = 1·3·6=en1.eln3.eln6+ 2. adım: el1.eln3.eln6 = el In1+In3+In6 + 3. adim: e In1+In3+In6 eln18 = In 18 4. adım:) e' = eln(8 + 10) 5. adım: eln(8+10) = e In8+In 10 6. adım: e' In10 = eln8.elr 7. adim: eln8.eln 10 = 8-10 = 80 Bu işlemler sonucunda Görkem, 18 = 80 sonucunu elde etmiştir. Buna göre, Görkem numaralandırılmış adımların han- gisinde hata yapmıştır? A) 2 B) 3 14 D) 5 E) 6 In8+In10 dakika 8.

A) 1440 6.2 109 23 16. 1 15 282 300 118 49154 (174 6-2204 B) 1120 12. le 13 109100 10. -248- 17 C) 1080 ho xlogx - 10x = 0 denkleminin farklı köklerinin çarpımı kaçtır? A) 1 B) 5 C) 10 D) 20 3% X/ogx loge 36 1 37 28 13 e 16x 75 D) 560 2 E) 540 1||3 X=1 * E) 100 =ox 10=10x Diğer sayfaya geçiniz.

18. Logaritma konusunun işlendiği bir matematik dersinde, Cem PF sırasıyla aşağıdaki adımları takip ederek işlemler yapmıştır. 1. 8 = 1.2.4 = 10log1.10log2 10log4 II. 10log1.10log2 10log4 = 10log1 + log2 + log4 10log1 + log2 + log4 = 10/098/ IV. 10log8 = 10log(4 + 4) + log4 = V. 10log(4+4) 10log4 VI. 10log4 + log4 = 10log4.10log4 VII. 10log4 10log4 = 4.4 = 16 Bu adımlar sonucunda Cem, 8 = 16 sonucunu elde etmiştir. Buna göre, Cem numaralandırılmış adımların hangisinde hata yapmıştır? - A) II ||| C) IV ⒸV E) VI

CAP [AB] doğru parçası x- eksenine paralel ve 1 < IABI < 50 olduğuna göre, B noktasının apsisi kaç farklı tam sayı değeri alabilir? A) 20 B) 22 C) 23 D) 24 E) 25 15. a ve b gerçel sayıları için a b=27 log3 = 5 Log 3 eşitlikleri veriliyor. Buna göre, loga² + log³b³ toplamının değeri kaçtır? A) 28 30 C) 32 0 34 E) 36 a2 1 Lonzo lag 3½v 32211 !! 1413 v (Wilay lay hog ib log +3 - act JA Diğer sayfaya geçiniz 36 bey 3 27 2 3 logz consistens 3 cab

18. m ve n birer gerçel sayıdır. f(x) = log, (mx-3), x < 3 2, x = 3 n-log(x-1)(x + 1), x>3 fonksiyonu tanımlı olduğu aralıktaki tüm gerçel sayı değerleri için sürekli olduğuna göre, m.n çarpımı kaçtır? A) 12 B) 16 C) 20 D) 24 E) 28 lim Six) = lim fex) = f(3) X-3+ X-3° (3m-3) los 3 = 2 3 (m-1) 21 1082 ^nedogn" (27) log₂ log Q = 3 3(m-1)= 82 ·m = 4 / 10p(29) 2 2 2^ = 4 2²=16 (n=4₂) min= ? 4.4=16 20. 25

9. Üzerinde birimleri logaritma ile ifade edilen Şekil l'deki cetvel, A ve B noktalarından kırılarak Şekil Il'deki gibi bir üçgen elde ediliyor. log1000 log250 0 log50 A B 25% log250 log1000 B 50.4 G Şekil II Şekil Il'deki üçgenin kenar uzunlukları m, n, p ve m> m+n p> n olmak üzere işleminin işleminin sonucu p nedir? A) log40 B) log60 C) log200 C D) log 200 6x-27 10. f: RR ve f(x) = 3x² - 2x + 4 fonksiyonu veriliyor. RU 1000 Şekil I A Tog50 log 4₁ loga 125 E) 1000

eg 7. Bülent 5 tane özdeş karton bardağı iç içe koyarak bir masanın üzerine koyuyor. Bülent bardakların masanın zemininden yüksekliğini (2+ log125) cm olarak ölçüyor. Ardından bu bardakların üzerine 11 bardak daha ilave ediyor ve tüm bardakların masanın zemininden yüksekliğini (2 + 14log5) cm olarak ölçüyor. 16 bardak 5 bardak 2 bardak 2 + log125 iç içe geçen bardakların kenarları arasındaki mesafeler eşittir. Bülent, bu bardaklardan 2 tanesini aynı şekilde iç içe yerleştirirse bardakların masanın zemininden yüksekliği kaç cm olur? A) log4 B) log8 C) 2 D) 1 E) log2 11 0 = 2 6 budak 2 + 14log5

PRA Aşağıdaki şekilde (AH] = logy br. |FH] = logx br ve |BE| = 2 br olmak üzere, ABCD ve AHFE özdeş dikdörtgenleri verilmiştir. 0gx-100 hogy 12). (ogy bg x-100 B A logy H logx F x ve y birer tam sayı olmak üzere, boyalı bölgelerin alanları toplamının alabileceği en küçük tam sayı değeri kaç br², dir? A) 16 B) 12 C) 10 D) 8. E) 6 bogbooty), bogy loginoty logy 2

ecektir." ektir." tiğına göre rasıyla E log2 (loggx) = logą (log₂x) A olduğuna göre, (log, 2)2 ifadesinin eşiti kaçtır? sorusunu sırasıyla aşağıdaki adımları takip ederek çözmüştür; 1. Adım : log₂ (log₂x 3) = log2 (log,x) II. Adim : log₂ (x 3) = (log₂x)3 III. Adim: log₂x = (log₂x) IV. Adim:27 (log2x)³ = log₂x V. Adim: log₂x = A=> => 27 A³=A⇒ 27 A³-A=0 ⇒A. (27A²-1)=0 ⇒ A=0vA² = 27 A = 3√3 A = -3√3 log₂x > 0 olduğundan A 0 ve A#-3√3 olmalıdır. O halde A = 3√3 tür. VI. Adim: (log,2)² = log 4 = 2log 2 1 2 2 VII. Adım : 2 log₂x A 3√3 Buna göre, Arzu numaralandırılmış adımların hangisinde hata yapmıştır? A) I BY II C) IV D) V E) VI 8. Ge eşi ola iş A F F(

Buna göre, yaklaşık olarak kaç yıl sonra planlanan sayıya ulaşılabilir? (log(1, 2) = 0,08) B) 25 A) 22 C) 28 D) 30 E) 32 (03₂². (x+y) 2 2x - y = 81 14. x - y = log 3 log2 olduğuna göre, x + y toplamı kaçtır? A) 2 B) log34 D) 4 (14 lo 16 =81 (xxy))" 192 3/2 x+y E) log227 26=81 C) log38 (x+y) )

18. Kimya dersinde yeni konuya geçen Hakan Hoca tahtaya konu anlatımını ve formülleri yazıp sonrada o formüllerle ilgili örnek sorular çözecektir. ASİTLER-BAZLAR →→ pH çizelgesi 0 7 14 (0 < pH <7 iken asit, 7 < pH < 14 iken baz) pH = -log[H] • pOH = -log[OH-] pH + pOH = 14 [H+] [OH-] = 10-14 (Bu değerler 25 °C ve 1 atm basınçta geçerlidir.) Sonra tahtada yer kalmadığı için bunları silmiş ve örnek soruları çözmeye başlamıştır. Örnek 1: Örnek 2: [H] = 1.109 olan bir çözeltinin pH'si, pOH'si ve asit ya da bazlığı hakkında ne söylenir? [OH-] = 1.10-10 olan bir çözeltinin pH'si, pOH'si ve asit ya da bazlığı hakkında ne söylenir? Çözüm 1: Çözüm 2: pH = -log10⁹) pH=9 pOH + 9 = 14 13-10-10 pOH = 5 ve bu çözeltinin pH'si (7, 14) arasında olduğunda bazdır. Örnek 1'i öğrencilerine anlatarak çözen Hakan Hoca, Örnek 2'yi de öğrencisi Beyza'dan çözmesini istemiştir. Bu soruyu doğru çözen Beyza, sonuçları aşağıdaki- lerden hangisi gibi bulmuştur? A) pH=4 B) pH = 10 pOH = 10 Çözelti; Baz C) pH = 4 pOH = 10 Çözelti; Asit pOH = 4 Çözelti; Baz D) pH = 10 pOH = 4 Çözelti; Asit E) pH = 3 pOH = 10 Çözelti; Baz

14. Cisimlerin gram cinsinden kütlelerini 3 veya 9 tabanında logaritma değeri olarak hesaplayan özel bir ölçüm aleti ile kütlesi x gram olan özdeş 4 cisim aşağıdaki gibi tartılıyor. ►x gram log, 16 gr Ölçüm aletinin sonradan ekranında oluşan bir kırık nede- niyle logaritması alınan sayı ekranda belirmiyor. x gram ağırlığındaki bu cisimlerden 6 tanesi tartıldığında aşağıdaki durum gerçekleşiyor. 17 log, gr Buna göre, kırık olan yerde görünmeyen sayı kaçtır? A) 6 B) 8 C) 12 D) 16 E) 18 Ritim Matematik

10. Üzerinde 1 den 200 e kadar olan tam sayıların yazılı oldu- ğu bir cetvel türünde her n tam sayının 1 e olan uzaklığı logn birimdir. -log4 -log3 log2- 1 1 1 1 2 3 4 200 Bu cetvel ile bir kurşun kalemin uzunluğu farklı iki konum- da ölçülmüştür. 12 72 200 1. Konum 2. Konum Buna göre, x kaçtır? A) 18 B) 25 C) 30 D) 36 150 200 E) 42

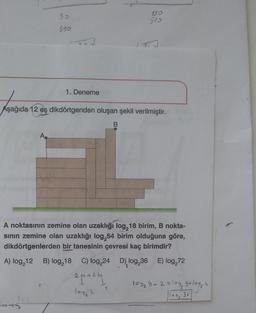
150 510 1. Deneme Aşağıda 12 eş dikdörtgenden oluşan şekil verilmiştir. B A. A noktasının zemine olan uzaklığı log,18 birim, B nokta- sının zemine olan uzaklığı log,54 birim olduğuna göre, dikdörtgenlerden bir tanesinin çevresi kaç birimdir? A) log₂12 B) log₂18 C) log,24 D), log,36 E) log₂72 20+25 1 log₂ 3 cary 30 330 1 109₂ 9+2 = log₂ g+10y₂4 loy 36