Maks. - Min. Problemleri Soruları
Lise Matematik
Maks. - Min. Problemlerigradb=6
6-
6
6-ano
cob
bare?
cob
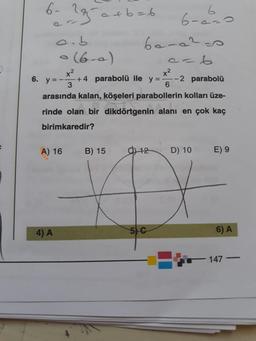
x2
x2
6.
y = --
+4 parabolü ile y = -2 parabolü
3
6
arasında kalan, köşeleri parabollerin kolları üze-
rinde olan bir dikdörtgenin alanı en çok kaç
birimkaredir?
• (6-0)
A) 16
B) 15
D) 10
E) 9
4) A
5 c
6) A
-147 -
![11. x bir tam sayı olmak üzere, bir ABC üçgeninde,
[AB] [AC]
EBOB(x² – 2x + 10, 2x² - 4x + 27) = 1
-
2
-
• m(ACB) = arcsin
=
X? - 2x + 10
-
V 2x² - 4x + 27
olduğuna göre, ABC üçgeninin çevresinin alabilece.
ği en küçük tam sayı değeri kaçtır?
A) 20
B) 18
C) 16
D) 15
E) 12
2
|2x²ux+27
4x - 8x4 sh
2x² - 4x
C](https://media.kunduz.com/media/question/seo/raw/20220213085334673965-3895879_KzygRzJeT.jpeg?w=256)
Lise Matematik
Maks. - Min. Problemleri11. x bir tam sayı olmak üzere, bir ABC üçgeninde,
[AB] [AC]
EBOB(x² – 2x + 10, 2x² - 4x + 27) = 1
-
2
-
• m(ACB) = arcsin
=
X? - 2x + 10
-
V 2x² - 4x + 27
olduğuna göre, ABC üçgeninin çevresinin alabilece.
ği en küçük tam sayı değeri kaçtır?
A) 20
B) 18
C) 16
D) 15
E) 12
2
|2x²ux+27
4x - 8x4 sh
2x² - 4x
C
Lise Matematik
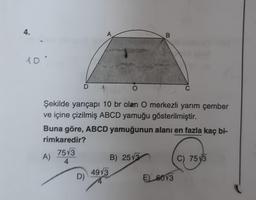
Maks. - Min. Problemleri4.
A
B
10'
D
O
C
Şekilde yarıçapı 10 br olan O merkezli yarım çember
ve içine çizilmiş ABCD yamuğu gösterilmiştir.
Buna göre, ABCD yamuğunun alanı en fazla kaç bi-
rimkaredir?
7573
A)
B) 253
4
C) 75y3
4913
D)
E) 6013

Lise Matematik
Maks. - Min. ProblemleriTÜREN
SORU 9
9
13 metre uzunluğundaki bir merdiven duvara dayalı olarak
durmaktadır.
duvar
Merdiven
Zemin
m/sn hızla ka
1
Merdivenin duvara değen ayağı duvardan
2
yarken merdivenin yere değen ayağı duvardan uzaklaşmak
tadır.
Merdivenin üst ucu yerden 12 m yükseklikteyken, merdi-
venin alt ucunun duvardan kaç m/sn hızla uzaklaştığını
bulalım.
6 sn
Cevap: m/s
5

Lise Matematik
Maks. - Min. ProblemleriBuna göre, bu araçlar harekete başladıktan kaç saat sonra
iki araç arasındaki uzaklik en az olur?
A)
3
5
B)
C1
D)
3
2
E) 2
50.50.2 + 2. (-100). (125 - 100x) -
50+ 200X-250-0
2008 200
= =1)
webouweg
8.
Alan=rria
360
20-25
Yukarıdaki şekilde çevresinin uzunluğu 20 cm olan küçük boy bir
pizzanın bir diliminin görünümü verilmiştir.
Bu pizzanın alanının en büyük olması için çapının uzunluğu
kaç cm olmalıdır?
A) 5
B) 8 C) 10 D) 15 E) 20
21
N

Lise Matematik
Maks. - Min. Problemlerienc
27. Aşağıda dikdörtgen biçiminde olan ve uzatılmak istenil-
diğinde Şekil 2'de görüldüğü gibi üst kısmı ortadan ikiye
ayrılarak içerisinden dikdörtgen biçiminde iki eş parça
çıkan bir masanın kısa ve uzun olduğu durumlardaki
görünümleri verilmiştir.
Boy
2
En
Şekil 1
Şekil 2
Masa Şekil 1'de gösterildiği gibi kısa durumdayken
dikdörtgen biçimindeki üst yüzeyinin çevre uzunluğu
80 cm'dir. Masa uzatıldığında üst yüzeyinin eni sabit
kalıyor ve boyu ilk duruma göre
oranında uzuyor.
4
Buna göre masa uzatıldığında dikdörtgen şeklinde-
ki üst yüzeyinin alanı en fazla kaç cm2 artar?
A) 88
B) 92
E) 108
D) 100
C) 96

Lise Matematik
Maks. - Min. ProblemleriANALIZ TESTİ - 6
7. Alanı 200 cm2 olan dikdörtgen şeklindeki
bir kartonun yan kenarlarından ikişer cm,
alt ve üst kenarlarından birer cm boşluk
bırakılarak oluşan dikdörtgensel bölgeye
resim yapıştırılıyor.
Resim yapıştırılacak bölgenin alanı
maksimum olduğunda kartonun çevre-
si kaç cm olur?
A) 90
B) 80
C) 72
D) 64
E) 60

Lise Matematik
Maks. - Min. Problemleri3. Kenar uzunluklan 20 cm ve 32 cm olan dikdört-
gen biçimindeki bir kartonun köselerinden bir
kenar uzunluğu x cm olan kareler kesilip atılıyor.
Geriye kalan kartondan sekildeki gibi prizma bici-
minde bir kutu oluşturuluyor.
X
X
X
X
X
Kutunun yan yüzlerinin alanları toplamının en
büyük değeri alabilmesi için x kaç olmalıdır?
A) 6
B) 7
C) 8
13
D)
15
2
E)
2.
30

Lise Matematik
Maks. - Min. Problemleri37. Sevinç, ortasında daire biciminde cam olan daire hal-
kası bicimindeki masasının alanını ölçebilmek için
cam kısmına T noktasında teñet olan bir çubuk koy-
muş ve çubuğun masanın dişında kalan kısımlarını
kesmiştir.
K
T
Çubuğun masa üzerinde kalan kısmını cetvelle ölç-
tüğünde 80 cm olduğunu tespit etmiştir.
Buna göre, cam hariç masanın üst yüzeyinin alanı
kaç desimetrekaredir?
A) 910
B) 107
C) 1210
D) 167
E) 3670

Lise Matematik
Maks. - Min. Problemlerib
Yukarıda verilen resimdeki gibi dikdörtgen biçiminde bir
bahçenin kısa ve uzun kenarlarının yarısına kadar duvar
örülmüştür.
Bahçenin duvar olmayan kenarlanna toplam 30 metre
uzunluğunda bir sıra tel örgü çekilmiştir.
Buna göre, bahçenin alanı en fazla kaç metrekare
olabilir?
A) 50
B) 75
C) 100
D) 125
E) 150

Lise Matematik
Maks. - Min. ProblemleriTÜREV
10. Bir mağazada 200 tane aynı cins oyuncak vardır.
Bir oyuncağın satış fiyatı 40 TL olduğunda tüm
oyuncaklar satılabilmektedir. Oyuncakların satış ti.
yatı 10 TL artırıldığında satılan oyuncak sayısı 20
tane azalmaktadır.
1.a
Buna göre, bu satıştan en çok kâr elde edebil-
mek için bir oyuncak kaç TL den satılmalıdır?
f
A) 50 B) 60
C) 70
D) 80
E) 90

Lise Matematik
Maks. - Min. ProblemleriHinda kesen
tafiği verilmiştir.
Buna göre, AABC) kaç birimkaredir?
B
C) 18
A) 12
D)
24
E) 30
2(-x+3)(x+2)
TX=3
=3
x=-
X=0
y=6
5.6.15 ,
9. f: RR
f(x) = x2 + 5x + 3
parabolü üzerinde alınan bir noktanın koordinatları top-
lamı en az kaçtır?
C) -4
A) -1
B)-2
D) -6
E) -8

Lise Matematik
Maks. - Min. Problemleri26.
X
X
2.
6a
Bir kenarı 6a cm olan kare şeklindeki bir kartonun
köşelerinden aynı büyüklükteki dört kare kesilerek
çıkartılıyor. Kalan kısım katlanarak dikdörtgenler prizması
şeklinde üstü açık ve en büyük hacimli bir kutu elde
ediliyor.
Buna göre, kesilen karelerin bir kenarının uzunluğu
cm cinsinden aşağıdakilerden hangisidir?
A)
5a
2
B) 2a
C)
37 Da
E)
E
Lise Matematik
Maks. - Min. ProblemleriYAYINLARI
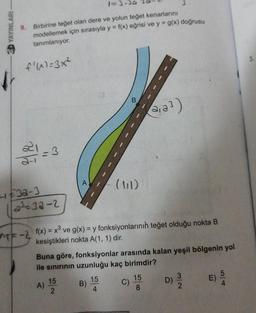
Birbirine teget olan dere ve yolun teğet kenarlarını
modellemek için sırasıyla y = f(x) eğrisi ve y = g(x) doğrusu
tanımlanıyor.
f'(x)=3x²
B
da?)
-3
2-1
A
HE32-3
12-32-2
ne-2 f(x) = x® ve g(x) = y fonksiyonlarının teğet olduğu nokta B
kesiştikleri nokta A(1, 1) dir.
Buna göre, fonksiyonlar arasında kalan yeşil bölgenin yol
ile sinirinin uzunluğu kaç birimdir?
5
D)
15
2
A)
15
4
15
8
E)
B)
C)
2

Lise Matematik
Maks. - Min. Problemleri2000 kişilik kapasitesi olan bir gösteri salonunda sergilenecek
bir tiyatro oyunu için bilet fiyatları 100 TL olarak belirlenmiştir.
Önceki tecrübeler dikkate alınarak bilet fiyatı 100 TL olduğun-
da tüm biletler satılacak iken bilet fiyatlarında yapılacak her 5
TL lik artışın 20 tane daha az biletin satılmasına sebep olaca-
ğı öngörülmektedir.
Buna göre, bilet fiyatı kaç TL olarak belirlenirse elde edi-
lecek hasılat en çok olur?
D) 300 E) 240
B) 360
C) 320
A) 400

Lise Matematik
Maks. - Min. Problemleri= 16
Bir fabrikada üretilen bir maddenin x tonunun maliyeti y bin TL
dir. x ile y arasında;
100
y = 4x +
X
bağıntısı olduğuna göre, maliyetin en az olması için bu
maddeden kaç ton üretilmesi gerekir?
A) 4 B) 5 C) 6 D7 E) 8
