Maksimum Minimum Problemleri Soruları

Lise Matematik
Maksimum Minimum Problemleri12. HAFTA KONU: İkinci Dereceden Fonksiyonlar (Parabol)
20. Koronavirus salgını nedeniyle oluşan günlük vaka sayısının zamana bağlı değişimi A ve B ülkelerinde aşağıdaki şekilde gözlemlenmiştir.
y (vaka sayısı)
y (vaka sayısı)
A Ülkesi
y=-2x² + 200x
x (gün)
Her iki ülkede de hastalık aynı anda ortaya çıkmıştır.
Buna göre,
1.
A ülkesinde günlük vaka sayısı en fazla 5000 olmuştur.
II. B ülkesinde vaka sayısının en fazla görüldüğü gün 100. gündür.
III. Her iki ülkede de vaka sayısının sıfıra indiği gün aynıdır.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) Yalnız II
rusuna göre simetrik y = mx² + nx + k pa-
11.SINIF
C) I ve II
y=-x+ 200x
B Ülkesi
D) I ve III
x (gün)
E) Il ve Ill
22. Aşağıda tepe noktası y ekseni üzerinde bulunan ve üstündeki
ndo olan bir dağ gösterilmiştir.

Lise Matematik
Maksimum Minimum Problemleri22. Bir atölyede ayda x tane elbise dikilmektedir ve her
X
elbisenin maliyeti 400 -
TL dir.
100
nipuoled
eisib
50
Elbiselerin tanesi 100+ TL den satıldığına
- 18
(A
göre maksimum kârın elde edilmesi için ayda
X
28
kaç elbise dikilmelidir?
A) 12000
B) 13000
D) 15000
C) 14000
E) 16000

Lise Matematik
Maksimum Minimum Problemleri10. Bir bölge, dikdörtgen şeklinde yan yana iki eş
oyun alanı oluşturulacak biçimde çitle çevrilecek-
tir.
b
a
D) 720
a
a
a
Buna göre, 120 metre çitle çevrilebilecek en
büyük bölgenin alanı kaç metrekaredir?
A) 450
B) 540
C) 600
b
E) 800

Lise Matematik
Maksimum Minimum Problemleri13. a, b, c ve d gerçel sayılardır.
RS2360
Yandaki tabloda şütündaki
sayılar yukarıdan aşağıya,
satırdaki sayılar soldan
sağa doğru büyümektedir.
B) 12
a
C) 15
5
d
n
Buna göre, (c+d)-(a+b) ifadesinin alabileceği en
büyük tam sayı değeri kaçtır?
A) 9
C d 10
D) 17
E) 18

Lise Matematik
Maksimum Minimum ProblemleriR VE UYGULAMALARI
en
19.
Parabol
Sorusu
11/A 40₂
AY
D
A
O
D) 4√3
C
B
TEST-3
y=x²+3
y=9
B) 212
X
Şekilde y = x² + 3 parabolü ve y = 9 doğrusu
verilmiştir.
Buna göre, ABCD dikdörtgeninin alanı en
çok kaç br² dir?
A) 12
blowigurn
Fureu bilmiyorum
11. Sınıfım
E) 5√2
C) 4√2

Lise Matematik
Maksimum Minimum Problemlerien
19.
D
A
C
D) 4√3
B
y=x²+3
y=9
B) 21/2
-X
TU
Şekilde y = x² + 3 parabolü ve y = 9 doğrusu
verilmiştir.
Buna göre, ABCD dikdörtgeninin alanı en
çok kaç br² dir?
A) √2
* Türev bilmizam
11. Sınıfım
E) 5√2
C) 412

Lise Matematik
Maksimum Minimum Problemleri15.
Duvar
16:
Bir tarafında duvar olan dikdörtgen şek-
lindeki bir bahçenin üç tarafına bir sıra tel
çekilecektir.
Kullanılan telin uzunluğu 160 m oldu-
ğuna göre, bahçenin alanı en çok kaç
metrekaredir?
A) 3200
D) 4000
B) 3400
E) 4800
C) 3600
18. m
pa
m
d
A

Lise Matematik
Maksimum Minimum ProblemleriYO-A
28
26.
27.
*18
* 52
1,5
200-2
Şekil -2
Şekil - 1
Yukarıda Şekil - 1'de verilen ve alanı 200 br² olan dikdörtgen
biçimindeki çerçevenin içine Şekil - 2'deki gibi bir poster yer-
leştirilmek isteniyor.
A) 144
Buna göre, yerleştirilecek olan posterin alanı en fazla
kaç br² olur?
B) 128
(200-2)(x-4)
200-2x800
-2x-800
>
X
C) 112 D) 108
+208
-2x²-800-20% x
AY
2,5
A
(1
18-3k
221
k
E) 100
100
5
26
-Ux+208=
208 = lit.
52 = x
;y=x
-2
(y = f(x)
6.

Lise Matematik
Maksimum Minimum Problemleri6. Bir bilgisayar satışında; x bilgisayar sayısını ve G bilgisayar satışından kazanılan geliri göster-
x²
500
mek üzere bilgisayar sayısına bağlı geliri gösteren ilişki, G (x)
bilgisayar satıldığında gelirin en fazla olacağını bulunuz.
==
+ 20x olduğuna göre kaç
qv

Lise Matematik
Maksimum Minimum Problemleri4.
Dikdörtgen şeklindeki ABCD karton levhasının mavi taralı kı-
sımları kesilip atılarak kapalı bir kutu yapılacaktır.
XLL
F
A
DX E
D) 4-√√3
|DF| = |DE| = x br, |AB| = 24 br ve |BC| = 12 br olduğuna
göre, kutunun hacminin en büyük olmasını sağlayan x de-
ğeri kaç birimdir?
A) 2+√3
B) 4 + √√3
C
E) 6+√3
B
C) 6-2√3
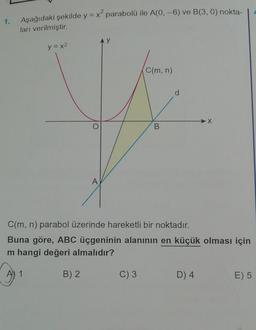
Lise Matematik
Maksimum Minimum Problemleri1.
Aşağıdaki şekilde y = x² parabolü ile A(0, -6) ve B(3, 0) nokta-
ları verilmiştir.
C(m, n)
#
B
1
y = x²
O
C(m, n) parabol üzerinde hareketli bir noktadır.
Buna göre, ABC üçgeninin alanının en küçük olması için
m hangi değeri almalıdır?
B) 2
C) 3
-X
D) 4
E) 5
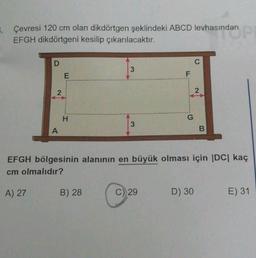
Lise Matematik
Maksimum Minimum ProblemleriÇevresi 120 cm olan dikdörtgen şeklindeki ABCD levhasından
EFGH dikdörtgeni kesilip çıkarılacaktır.
indan pr
D
A) 27
2
A
E
H
3
B) 28
3
F
C) 29
G
EFGH bölgesinin alanının en büyük olması için |DC| kaç
cm olmalıdır?
C
D) 30
2
B
E) 31

Lise Matematik
Maksimum Minimum ProblemleriAşağıdaki şekilde görülen ABCD dikdörtgeninde
|DE| = |DF|, |AB| = 20 br ve |BC| = 12 br
olarak veriliyor.
LL
D
A
E
20
B) 138
C) 140
C
Buna göre, boyalı bölgenin alanının en büyük değeri kaç
br² dir?
A) 130
D) 142
B
12
E) 145
000
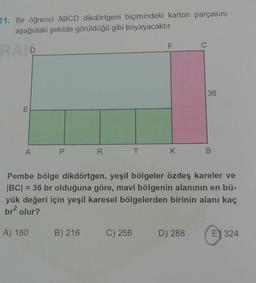
Lise Matematik
Maksimum Minimum Problemleri11. Bir öğrenci ABCD dikdörtgeni biçimindeki karton parçasını
aşağıdaki şekilde görüldüğü gibi boyayacaktır.
RAIP
A
R
B) 216
T
C) 256
F
K
Pembe bölge dikdörtgen, yeşil bölgeler özdeş kareler ve
|BC| = 36 br olduğuna göre, mavi bölgenin alanının en bü-
yük değeri için yeşil karesel bölgelerden birinin alanı kaç
br² olur?
A) 180
C
D) 288
36
E) 324

Lise Matematik
Maksimum Minimum ProblemleriDik koordinat düzleminde, OBKD karesi ile ADK ve KBE dik
üçgenleri veriliyor.
A
D
y
K
B
E
X
8
A(0, 12) ve E(16, 0) olduğuna göre, boyalı bölgelerin alan-
ları toplamının en büyük değeri kaç br² dir?
A) 45
B) 48
C) 49
D) 50
E) 54
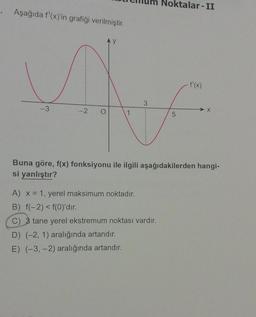
Lise Matematik
Maksimum Minimum ProblemleriAşağıda f'(x)'in grafiği verilmiştir.
Ax
3
1
-3
Noktalar-II
A) x = 1, yerel maksimum noktadır.
B) f(-2) < f(0)'dır.
C) 3 tane yerel ekstremum noktası vardır.
D) (-2, 1) aralığında artandır.
E) (-3,-2) aralığında artandır.
5
X
Buna göre, f(x) fonksiyonu ile ilgili aşağıdakilerden hangi-
si yanlıştır?
