Parabol Soruları
![5.
Aşağıda orijinden geçen, y=2.n.x2 parabolü çizilmiştir.
7.
f(x)=x2- 4x-
parabolü x eksenini
m'nin alabileceği e
kaçtır?
AY
ly=2.n.x2
A) 4
B) 5
A
B
--5
-1
O
[AB]1[AO] olduğuna göre, n kaçtır?
16
1
C)
4
D)
A) 1 B)
12
8
2](https://media.kunduz.com/media/question/seo/raw/20210328153957746163-2151995_FfvHmXE5y.jpg?w=256)
Lise Matematik
Parabol5.
Aşağıda orijinden geçen, y=2.n.x2 parabolü çizilmiştir.
7.
f(x)=x2- 4x-
parabolü x eksenini
m'nin alabileceği e
kaçtır?
AY
ly=2.n.x2
A) 4
B) 5
A
B
--5
-1
O
[AB]1[AO] olduğuna göre, n kaçtır?
16
1
C)
4
D)
A) 1 B)
12
8
2
Lise Matematik
ParabolYX+4
Yayin
2.
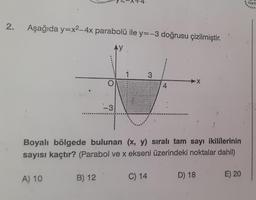
Aşağıda y=x2-4x parabolü ile y=-3 doğrusu çizilmiştir.
AY
1
3
X
4
-3
Boyalı bölgede bulunan (x, y) sirah tam sayı ikililerinin
sayısı kaçtır? (Parabol ve x ekseni üzerindeki noktalar dahil)
A) 10
E) 20
C) 14
B) 12
D) 18
Lise Matematik
ParabolA
A
ÇAP / AYT - 2 / Matematik Testi
14.
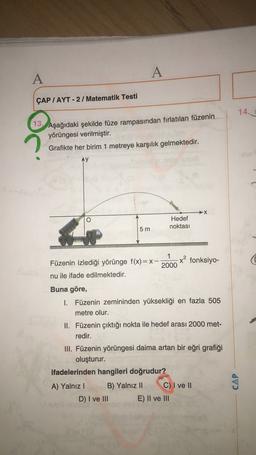
13. Aşağıdaki şekilde füze rampasından fırlatılan füzenin
yörüngesi verilmiştir.
Grafikte her birim 1 metreye karşılık gelmektedir.
Ay
→X
Hedef
noktası
5 m
1
x? fonksiyo-
2000
Füzenin izlediği yörünge f(x)= X-
nu ile ifade edilmektedir.
Buna göre,
I. Füzenin zemininden yüksekliği en fazla 505
metre olur.
II. Füzenin çıktığı nokta ile hedef arası 2000 met-
redir.
III. Füzenin yörüngesi daima artan bir eğri grafiği
oluşturur.
ifadelerinden hangileri doğrudur?
A) Yalnız! B) Yalnız 11 C) I ve II
D) I ve III E) II ve III
CAP
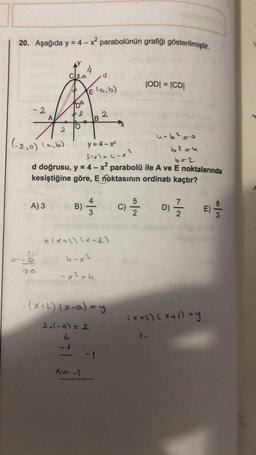
Lise Matematik
Parabol20. Aşağıda y = 4 - x parabolünün grafiği gösterilmiştir.
4
d
JODI = |CD|
Elaib)
Da
- 2
2
O
2
(-2,0) (a,b)
y = 4 - X2
u-6²-
b2=u
flon nax?
d doğrusu, y = 4 - x? parabolü ile A ve E noktalarında
kesiştiğine göre, E noktasının ordinatı kaçtır?
A) 3
B)
-
C)
D)
1 / 1
3
E)
alx+2)(x-2)
- 5 k-x2
- x2th
.(X+2) (x-a)=y
(x+2)(x+0) sy
2.(-a)=2
Al
![10. Geyçel sayılar kümesi üzerinde tanımlıf ve g fonksiyonlari-
porn grafikleri aşağıda verilmiştir.
g(x) = x2 – 4
f(x) = x2 – 1
IL
D
C
2
3
g(a)=a
A
B
f(x) = x² - 1 ve g(x) = x² - 4 olduğuna göre, A ve B köşe-
leri g(x) parabolü üzerinde ve [DC] kenarı f(x) parabolü-
nün tepe noktasında bulunan karenin alanı kaç birimka-
redir?
A) 6-27
B) 6 + 277
C) 9
D) 4
E) 7 + 216](https://media.kunduz.com/media/question/seo/raw/20210507124935549118-2104569_Vl0ySvvDh.jpg?w=256)
Lise Matematik
Parabol10. Geyçel sayılar kümesi üzerinde tanımlıf ve g fonksiyonlari-
porn grafikleri aşağıda verilmiştir.
g(x) = x2 – 4
f(x) = x2 – 1
IL
D
C
2
3
g(a)=a
A
B
f(x) = x² - 1 ve g(x) = x² - 4 olduğuna göre, A ve B köşe-
leri g(x) parabolü üzerinde ve [DC] kenarı f(x) parabolü-
nün tepe noktasında bulunan karenin alanı kaç birimka-
redir?
A) 6-27
B) 6 + 277
C) 9
D) 4
E) 7 + 216
Lise Matematik
Parabolda,
9. Şekilde f(x) = x2-mx + m + 15 parabolü ile x eksenin
paralel d doğrusu y ekseni üzerindeki A noktasınd
an
kesişmektedir.
y = f(x)
d
A
O
X
2
f(x) parabolü x eksenine teğet olduğuna göre, AOB
üçgeninin alanı kaç birimkaredir?
A) 18
B) 24
C) 27
D) 32
E) 36
5.A 6.D
7.C
8.B 9.C

Lise Matematik
Parabol2. r pozitif bir gerçek sayı olmak üzere, dik koordinat düzle-
minde orijinden geçen
f(x) = (x - r)2 - 4
parabolü kullanılarak,
00
f(x - 1) -
(-4)
f(x - 2) +r
biçiminde tanımlanan iki parabolün tepe noktaları ara
sindaki uzaklık kaç birimdir?
A) 4
B) V17
C) 312
D) 275
E) 1/6

Lise Matematik
Parabolİkinci Dereceden Fonksiyonlar (Parab
1.
y
Şekilde y=fx) parabolü veril
miştir.
y = f(x)
13
Parabolün y eksenini kestiği
noktanın ordinatı kaçtır?
0
4
y=c
T(2,-5)
7
B)
C) -3
D)
A-4
Njo
E)-2
2
2.
f(x) = 4x2 - (3 - m)x + 6
Lise Matematik
Parabol2. Aşağıdaki şekilde tepe noktası T(r, k) olan y=f(x) para-
bolü ile x+2y=2 doğrusu A ve B noktalarında kesişmek-
tedir.
y
T
k.
A
-1
3
→X
r
B
X+2y=2
y=f(x)
Buna göre, parabolün tepe noktasının koordinatları
toplamı kaçtır?
7
A) 2
B) 3
E
3

Lise Matematik
Parabol9. m ve n gerçek sayılar olmak üzere
f(x) = x2 - (m - 6)x+ n + 1
fonksiyonu her x gerçek sayısı için
ilen
f(3 + x) = f(3-X)
eşitliğini sağlamaktadır.
Buna göre, m kaçtır?
S
A) 12
B) 13
C) 14
D) 15
E) 16
10.
y = x2 + 2x + 1

Lise Matematik
Parabol3.
y = x2 - 2x - 6
parabolü üzerinde apsisi ile ordinatı toplamı sıfır
olan noktalar arasındaki uzaklik kar birimdir?
6. f:
A) 3/2
B) 5
C) 572
fon
mir
kad
D) 6
E) 6/2
A)
x-2x 6 = ax
*+2x-6ex
x²+x-6
2.

Lise Matematik
ParabolPOLINOMLAR
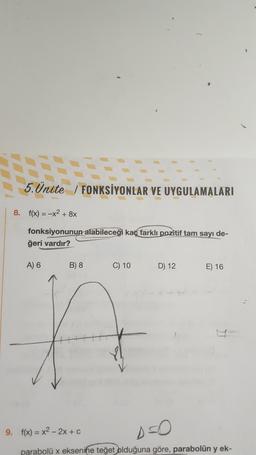
3. Bir f(x) fonksiyonuna hangi yönde öteleme yapıldığında hangi
fonksiyonun elde edileceği aşağıda gösterilmiştir.
a br.
a br.
a br.
sola yukan aşağı
f(x + a) f(x) + a f(x) - a
a br.
sağa
f(x - a)
Buna göre,
f(x) = x2 + 4x + 3
parabolüne hangi öteleme hareketleri uygulanırsa
g(x) = x2 + 1
parabolü elde edilir?
A) 2 birim sola 1 birim yukarı
B) 2 birim sağa 2 birim yukarı
C) 2 birim sağa 2 birim aşağı
D) 2 birim sola 2 birim yukarı
E) 1 birim sağa 2 birim aşağı
Lise Matematik
Parabol1
5. Ünite / FONKSİYONLAR VE UYGULAMALARI
S.Ünite /
8. f(x) = -x2 + 8x
fonksiyonunun alabileceği kaç farklı pozitif tam sayı de-
ğeri vardır?
A) 6
B) 8
C) 10
D) 12
E) 16
A
9. f(x) = x2 - 2x + c
parabolü x eksenine teğet olduğuna göre, parabolün y ek-

Lise Matematik
ParabolBuna göre, A noktasınin koordinatları toplamı
kaçtır?
x²g = ax - b
B) - 7
C) - 8
E) - 12
A) - 4
2) - 9
EL
-1,-8
12. Aşağıda y = f(x) parabolü çizilmiştir.
y=6
4 y
x²2x-3-2
-
2x 6
x=3
x=-1
3
()
+²+3
y = f(x)
3=2
1
4
X
23
Buna göre, f(2a) = 2 eşitliğini sağlayan a değerleri-
nin çarpımı kaçtır?
B)
3
A)
2
1
W/N
C)
1
D)
-
E)
_1²3
4
2
7.D
8.D 9.B 10.E 11.D 12. E
![4.
E
M
G
A
B
N
IR
seni
D K FT C
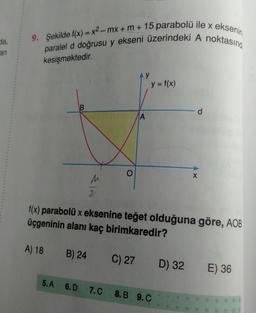
Yukarıdaki şekilde bir pencerenin genel görüntüsü
verilmiştir. Bu pencerenin üst kısmı bir parabol şek-
lindedir. Alt kısmı ise dört parçaya bölünmüş ABCD
dikdörtgenidir. [EF] doğrusu [AB] ve [DC] doğrularını
dik bir şekilde ortadan kesmektedir.
Bu pencerenin kenarları ile ilgili;
ABI = 240 cm
IEF] = 180 cm
INK) = 120 cm
|ANI = |NG| = |GR| = |RB|
[MK] // [EF] // [PT]
olduğu bilinmektedir. Bu pencere analitik düzleme
aşağıdaki gibi konumlandırılmaktadır.
y
şek-
M
B
A
→ X
DK FTC
Buna göre, M noktasının koordinatları aşağıdaki-
lerden hangisidir?
A) (30, 60)
B) (45, 60)
C) (60, 30)
D) (60, 45)
E) (60, 40)
ur.
duğuna](https://media.kunduz.com/media/question/seo/raw/20210407000522941967-2362483_LX7UMDAFe.jpeg?w=256)
Lise Matematik
Parabol4.
E
M
G
A
B
N
IR
seni
D K FT C
Yukarıdaki şekilde bir pencerenin genel görüntüsü
verilmiştir. Bu pencerenin üst kısmı bir parabol şek-
lindedir. Alt kısmı ise dört parçaya bölünmüş ABCD
dikdörtgenidir. [EF] doğrusu [AB] ve [DC] doğrularını
dik bir şekilde ortadan kesmektedir.
Bu pencerenin kenarları ile ilgili;
ABI = 240 cm
IEF] = 180 cm
INK) = 120 cm
|ANI = |NG| = |GR| = |RB|
[MK] // [EF] // [PT]
olduğu bilinmektedir. Bu pencere analitik düzleme
aşağıdaki gibi konumlandırılmaktadır.
y
şek-
M
B
A
→ X
DK FTC
Buna göre, M noktasının koordinatları aşağıdaki-
lerden hangisidir?
A) (30, 60)
B) (45, 60)
C) (60, 30)
D) (60, 45)
E) (60, 40)
ur.
duğuna

Lise Matematik
Parabol.
iki öğrenci aşağıdaki iki grafiği çizmiştir.
Mehmet: y = x2 - - 1
Soner: y = 2(x2-x-1)
Buna göre,
1 Mehmet'in grafiği x eksenini hangi iki noktada
kesiyorsa Soner'in grafiği de x eksenini o ik
noktada keser.
II. Sonerin grafioinde parabolün kolları birbirine
daha yakındır.
JK: Soner'in grafiği, Mehmet'in grafiğinin 2 birim
aşağı otelenmiş biçimidir.
yargıllarından hangileri doğrudur?
A) Yalniz
B) Yalniz II
C) Yalnız i
D) 1.8
E) I, III
12.
