Permütasyon Soruları

Doğal Sayılar olmak üzere, tır? 16 E) 18 (2016-YGS) lmak üzere; inin çarpım ağlayan üç n rakamları Doğal Sayılar... 61 ((n + 1)² + (n!)² [(n+1)!]²-(n!)² 60 olduğuna göre, n kaçtır? A) 9 B) TO C) 12 D) 13 E) 15 (2013-YGS) (n+1) +11+0₁ ₁² nt (+1)| (0+1)! -^/^! (n+¹) n! (+²) n) + ^!^! (^+1)^! (n+¹)^²-^!^! E. BOLUNE 1. AABA Buna göre A AT 88

26. Bir çiçekçi her birinden elinde tek tür olan lilyum, gül, papatya ve lalenin de olduğu sekiz çeşit çiçekten istenilen kadar türü istenilen sayılarda birleştirerek çiçek buketi oluşturmaktadır. Bir müşteri aşağıdaki gibi bir buket hazırlatmak istiyor. Bukette toplam beş tür çiçekten 5 adet olsun. Gül ile lale aynı bukette bulunmasın. Bukette kesinlikle lilyum bulunsun. ● Buna göre, bu çiçekçi müşterisinin istediği gibi kaç farklı buket hazırlayabilir? A) 20 B) 25 C) 30 D) 35 E) 40

21. 3 raftan oluşan bir ki- taplığın en üst rafında eş 3 kitap, orta rafında eş 2 kitap, en alt rafin- da ise eş 2 kitap bulun- maktadır. Kitaplıktaki tüm kitapları okumak isteyen bir kişi kaç farklı sırayla kitapları okuyabilir? A) 36 B) 80 C) 120 D) 180 E) 210

11:07 T LTÉ 11. Her biri 5 seçenekli 8 soruluk bir testin cevap anahtarında art arda gelen herhangi dört sorunun cevabı sadece bir kez aynı şık olmuştur. 276 (15). 15678 24 6 Test-3 ÖRNEK BİR CEVAP ANAHTARI 1.G 2.B 3.B 4.B 5.B 6.A 7.E 8.D SPE BANAAL T2 Her şık testte en az bir sorunun cevabı olduğuna göre, cevap anahtarı kaç farklı şekilde hazırlanabilir? A) 300 B) 400 C) 500 D) 600 24₁5=120 E) 640 Test 14.

7. Faktörlyel; 1 den n'ye kadar olan sayma sayıların çar- pimina n faktörlyel denir ve n! şeklinde gösterilir. Ömeğin; nl = 1.2.3.....(n-1).n 21=1.2 31=1.2.3 41=1.2.3.4= 31.4 ifadesinin değeri kaçtır? B) 10 C) 19 D) 110 11! + 10! 91 A) 9 E) 120

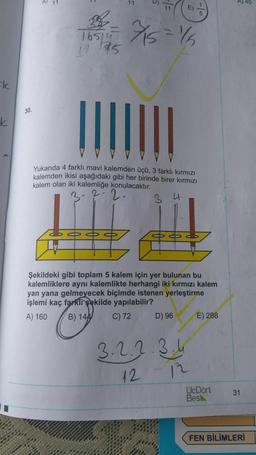
#k 30. A 11 11 11 E) 23 = ¾/15=15 38 16514 1175 Yukarıda 4 farklı mavi kalemden üçü, 3 farklı kırmızı kalemden ikisi aşağıdaki gibi her birinde birer kırmızı kalem olan iki kalemliğe konulacaktır. 3 4. 000 Şekildeki gibi toplam 5 kalem için yer bulunan bu kalemliklere aynı kalemlikte herhangi iki kırmızı kalem yan yana gelmeyecek biçimde istenen yerleştirme işlemi kaç farklı şekilde yapılabilir? A) 160 B) 144 C) 72 D) 96 3.2.2.3.4 12 5 12 E) 288 UcDört Bes A) 40 31 FEN BİLİMLERİ

Şekilde 1x5 boyutunda 5 özdeş kareden oluşan blok veriliyor. Şekildeki blok; 1x3 boyutunda de, 1x2 boyutunda tunda koşuluyla kapatılıyor. Örnekler: biçimin- biçiminde ve 1x1 boyu- biçimindeki bloklarla üst üste gelmemek Y+P=3 Y+K=2 K+P = 4 (A) 11 6 Buna göre, verilen bloklar kullanılarak 1x5 boyu- tundaki blok kaç farklı şekilde kapatılabilir? B) 13 C) 15 D) 17 E) 23

22 12:55 TYT 29. Aşağıda verilen renkleri dışında özdeş olan 4 tahta parçası saat yönünde A, B, C ve D noktaları etrafında 90 ar derece dönebilmektedir. B 1 A A) 6 B L B Buna göre 4 tahta parçası toplam 180 döndürüldüğünde kaç farklı görüntü oluşur? B) 10 5.0 C) 15 D) 18 E) 21 : x 0

15. Bir sayının okunuşu ile tersten okunuşu aynı ise bu sayıya "palindrom sayı" denir. Örneğin, 53235 ve 7117 sayıları palindrom sayılar- dır. Buna göre rastgele yazılan 5 basamaklı bir do- ğal sayının palindrom sayı olma olasılığı kaçtır? B) 1 C) 100 D) 1 180 Sto, t0,11 2,10-10.10.10 E) 1 200 17. Gerçe dan f eşitli Bun lim

SM 24. 5 mühendis ve 4 teknisyen bitirdikleri projenin önünde yanyana durarak hatıra fotoğrafı çektire- ceklerdir. Aşağıda belirtilen şekilde poz verilecektir. Mühendis ve teknisyenler olarak iki gruba ayrı- lip gruplardan biri önde diğeri arkada duracaktır. Baş mühendis Selim Bey, mühendis grubunun ortasında yer alacaktır. Bu koşullara uygun kaç farklı şekilde yan yana durarak fotoğraf çektirebilirler? A) 4!. 4! B) 2.4! D) 2.4!-4! C) 2.4! 5! E) 4! -5!

8. 5 kişi gezi için A, B, C ve D ülkelerine gidecektir. Bu ülkelerin her birine en az birer kişi gideceğine göre, bu 5 kişi kaç farklı gruplama ile gidebilir? A) 60 Ar B) 120 C) 240 81 (0 D) 360 E) 720 BA $SUPARA

arak 417 , k) iç k 14 3 adet 100 TL lik banknot, 5 çocuğa her çocuğa istenen sayıda vermek koşuluyla kaç farklı şekilde dağıtılabilir? A) 25 5 3 = B) 30 C) 35 - D) 40 bu kişiler yer TL verdik. değiştirdi 10 Herhangi 3 öğrenciye birer tane dağıttık. (5)2-20 Herhangi 2 öğrenciden birine 2 Permitasyon tane 100 TL, diğerine 1 tane 100 girmez mi? neden Sinalıyer? E) 45 (5) 10+20+5 = 35 farklı şekilde dağıtabilir. 5 Herhangi bir öğrenciye 3 tane 100 TL verdik. Yanıt C

16 TETRA ³3,53 Sayısal 120% Sözel 150 Eşit ağırlık Yandaki grafik 960 öğrencinin bulun- duğu bir okulda öğrencilerin okuduk- lan bölümlere göre oluşturulmuştur. 1440360 4x21 360 150 960 X400 C) 250 96 153 D) 300 480 1440 Buna göre, bu okulda bir eşit ağırlık öğrencisi kaç farklı bi- çimde seçilebilir? A) 190 B) 200 +96 E) 400

15. kümesi 1, 2, 3, 4 rakamları kullanılarak oluşturulan ve rakamları birbirinden farklı olan dört basamaklı bütün do- ğal sayıların kümesidir. U nun elemanlarından 4 rakamı 1 rakamının solunda olanlar A kümesini, 4 rakamı 2 raka- mının sağında olanlar B kümesini oluşturuyor. ANDER Buna göre, A B kümesinin eleman sayısı kaçtır? A) 12 B) 16 C) 18 D) 20 E) 24 4 1 24 Ⓒ+2=8

13. Merve ve Sefer çiftinin evlerinde düzenlediği davete 3 evli çift katılmıştır. Davetin sonunda düz bir sıra boyunca çekilecek hatıra fotoğrafında misafir çiftlerde eşler yan yana olacağına göre, kaç farklı şekilde fotoğraf çektirebilirler? A) 960 B) 720 C) 384 D) 360 E) 120

2019 - TYT 28. Aşağıda bir sinema salonunun koltukları gösterilmiş- tir. işaretiyle gösterilen koltuklar dolu, ile gösterilen koltuklar boştur. Koltukların doluluk durumu şekildeki gibiyken sine- maya gelen üç arkadaş yan yana oturmak istemek- tedir. Buna göre, üç arkadaş kaç farklı şekilde yan yana oturabilir? A) 5 B) 16 C) 24 D) 42 E) 48 A C 1 L Y A Y N L A