Rutin Olmayan Problemler Soruları

Lise Matematik
Rutin Olmayan Problemler1. Bu testte 40 soru vardır.
2. Cevaplarinizi, cevap kâğıdının Temel Matematik Testi için ayrılan ki
3.
1.
11
5.2
L
işlemi
A) -9
Doğanay, Tuna, Alperen ve Emir isimli dört arka-
daş bir pizza salonunda ortak bir pizza söylemiş-
ler, bu pizzayı yedikten sonra ikinci pizzayı, ikinci
pizzayı yedikten sonra üçüncü pizzayı söylemiş-
lerdir.
20
-22
bo G C
1
Doğanay 1. pizzanın ünü, 2. pizzanın
4
ünü, 3. pizzanın ini yemiştir.
5
en
22
ünü, 3.
1
Tuna 1. pizzanın ini, 2. pizzanın
5
1
pizzanın sini yemiştir.
6
1
4.
Alperen 1. pizzanın sini, 2. pizzanın ünü,
2
yemiş, 3. pizzadan yememiştir. 2016
6c be
Emir, Doğanay, Tuna ve Alperen'den geriye
kalan tüm pizzaları yemiştir.
3+20 +38
GO TO...6
Üç pizza da birbirine eştir
.
21 L
gwNR.
3
+
eşi
A)
Buna göre, Emir'in yediği pizzaların toplamı 1
pizzanın kaçta kaçıdır?
13 4
17 53 59
A) B) C)
E)
5
20 60 60
20
Doğanay
+
20+ 22
Tuna Alperen Emir
*****
22
3024
to 60
be
be 60

Lise Matematik
Rutin Olmayan ProblemlerA)
uy
2p
34 LP
6402442
Çiftçi Hüseyin Amca, serasında aynı sıra üzerine diktiği doma-
tes ve salatalık fidelerini yerden tavana doğru aynı uzunlukta-
ki iplerle bağlamıştır.
Hüseyin Amca,
• elinde yeterli ip olmadığı için yanyana bulunan her iki fi-
deyi iplerden biri ortak olacak şekilde bağlamıştır.
• her bir salatalık fidesi için 3, her bir domates fidesi için 2
ip kullanmıştır.
• dikilen salatalık fidesi sayısı, domates fidesi sayısının 3 ka-
tindan 2 fazladır.
Hüseyin Amca, bu fideleri bağlamak için toplam 75 parça ip
kullandığına göre, dikilen salatalık fidesi sayısı, domates fi-
desi sayısından kaç fazladır?
A) 18
B) 30
C) 22
D) 26
E) 30
Bu
#matematigiseviyorum

Lise Matematik
Rutin Olmayan Problemler1. Bir alışveriş merkezinde bulunan eşya koyma dolabı-
nin bazı gözleri aşağıda gösterilmiştir.
3. Bir
etti
1
3
5
A
Bu
da
2 4 6
C
B
2x
Dolap alt raf ve üst raf olmak üzere iki raftan oluş-
maktadır.
Üst raftaki dolaplar soldan sağa doğru ardışık tek
sayılarla, alt raftaki dolaplar soldan sağa doğru
ardışık çift sayılarla numaralandırılmıştır.
Üst rafta ve alt rafta eşit sayıda dolap bulunmak-
tadır.
Alt raftaki en sağda bulunan dolabın numarası
B'dir.
• Alt raftaki tüm dolapların numaraları toplamı üst
raftaki tüm dolapların numaraları toplamından 40
fazladır.
B dolabı ile C dolabı arasında 5 dolap vardır.
A
100
15
ral
Buna göre, A dolabının numarası kaçtır?
D) 65
E) 67
A) 59
B) 61
C) 63
Tum
B
S
24
A
A

Lise Matematik
Rutin Olmayan Problemler21.
ener
man gözlu
sanisin
cahara
Olona
M = {Mavi gözlü doktorlar}
K= {Kahverengi gözlü doktorlar}
S = {Sarışın doktorlar}
E = {Esmer doktorlar}
kümeleri veriliyor.
Buna göre, (S U M) (E U K) kümesi aşağıdakilerden
hangisidir?
A) Sarışın ve kahverengi gözlü doktorlar
Sarışın ve mavi gözlü doktorlar
C) Esmer olmayan kahverengi gözlü doktorlar
D) Sarışın olmayan mavi gözlü doktorlar
E) Esmer ve kahverengi gözlü doktorlar
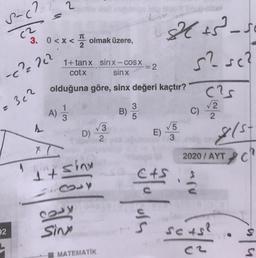
Lise Matematik
Rutin Olmayan Problemler2
s-c?
(²
TT
3. 0<x<
olmak üzere,
es - so
s? sc?
1+tanx sin x - COS X
cotx sin x
-=2
-c²2 222
olduğuna göre, sinx değeri kaçtır?
cas
c) 2
2 362
A)
1
B)
3
5
2
✓3
D)
2
E)
V5
3
&(st
2020 / AYT
ci
4
1t sin
CAS
Solon
29y
32
sing
sots?
est
MATEMATIK
S

Lise Matematik
Rutin Olmayan Problemler7.
Ali ile Cemre bir kutudaki bilyeleri aşağıdaki gibi paylaşt-
yorlar.
Ali'nin 1 bilye almasıyla paylaşıma başlanır.
Bilye alma sırası gelen kişi kendisinden önce alınan bil-
ye sayısının bir fazlası kadar bilye alır.
Ali 1 bilye alır, Cemre 2 bilye alır, Ali 3 bilye alır, Cemre
4 bilye alır ve kutudaki bilyeleri bu sıraya göre payla-
şırlar.
Kutuda yeterli sayıda bilye kalmadığı durumda sırası
gelen kişi kutuda kalan tüm bilyeleri alır ve paylaşım
işi biter.
Ali toplam 105 tane bilye aldığına göre, Cemre toplam
kaç tane bilye almıştır?
A) 102
B) 104
C) 106
D) 108
E) 110

Lise Matematik
Rutin Olmayan Problemler28. Omer, aldior bir tatil kitabındaki derslere ait soru sayisini ve
bu derslerden günlük çözmesi gereken soru sayısını bir tab-
2
Fizik
Kimya Biyoloji
prase
va çekildeki gibi yazıyor
Türkçe
Kitaptaki soru
sayisi
Çözeceği gün-
25
lük soru sayısı
68
100
80
po
45
20
20
15
D
Her dersi farklı bir gün çoxmeye başlayan Ömer, başladığı
günden itibaren her gün tabloda belirtilen soru sayısı kadar
bu derslerden soru çözerek tüm kitabı 7 günde bitirmiştir.
28
Toplam soru sayısı
60
C
a
Gün
2 3 4 5 6
7
110
Yukarıdaki grafik Ömer'in günlük çözdüğü toplam soru
sayısı ile oluşturulduğuna göre, a + b + c toplamı kaç-
tir?
1201
A) 80
E) 119
B) 85
190
10g
2812
EDO
1204
Ooo
180 D
140
288
208610
200
21
27
Lise Matematik
Rutin Olmayan Problemlerxyz
B
B
Matematik
8. Aşağ
sind:
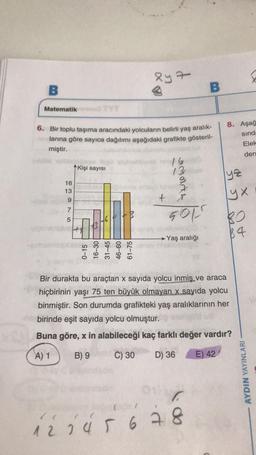
6. Bir toplu taşıma aracındaki yolcuların belirli yaş aralık-
larına göre sayıca dağılımı aşağıdaki grafikte gösteril-
miştir.
Elek
den
Kişi sayısı
16
13
lyz
16
13
+
9
7
B.
501
lyx
po
$4
5
os
→ Yaş aralığı
0-15
16-30
31-45
46-60
61-75
Bir durakta bu araçtan x sayıda yolcu inmiş ve araca
hiçbirinin yaşı 75 ten büyük olmayan x sayıda yolcu
binmiştir. Son durumda grafikteki yaş aralıklarının her
birinde eşit sayıda yolcu olmuştur.
Buna göre, x in alabileceği kaç farklı değer vardır?
A) 1
B) 9
C) 30
D) 36
E) 42
AYDIN YAYINLARI
12 ias
678
5 6
![5.
A, B, C illerindeki hava sıcaklıkları sırasıyla a, b, c derece 7.
olarak verilmektedir. Bu sıcaklık değerleri arasında
-] A
a<b< c
& S2
1 3
2
lbl < lal < 1c
eşitsizlikleri sağlandığına göre, aşağıdakilerden hangisi
kesinlikle doğrudur?
A) Ave B illerindeki sıcaklık sifilin altındadır.
B) B. ve Cillerindeki-stoaklikstfrir üstürtdedir.
C} B ilindeki sicaklik sifirin altında, Cilindeki sıcaklık sifirin
üstündedir
D) En fazla 2 itin sıcaktik değeri sifirin ustundedir.
E) Sıcaklık değeri sıfırın altında olan en az 2 il vardır.](https://media.kunduz.com/media/question/seo/raw/20210315164058724785-1277685_StpGefPsR.jpg?w=256)
Lise Matematik
Rutin Olmayan Problemler5.
A, B, C illerindeki hava sıcaklıkları sırasıyla a, b, c derece 7.
olarak verilmektedir. Bu sıcaklık değerleri arasında
-] A
a<b< c
& S2
1 3
2
lbl < lal < 1c
eşitsizlikleri sağlandığına göre, aşağıdakilerden hangisi
kesinlikle doğrudur?
A) Ave B illerindeki sıcaklık sifilin altındadır.
B) B. ve Cillerindeki-stoaklikstfrir üstürtdedir.
C} B ilindeki sicaklik sifirin altında, Cilindeki sıcaklık sifirin
üstündedir
D) En fazla 2 itin sıcaktik değeri sifirin ustundedir.
E) Sıcaklık değeri sıfırın altında olan en az 2 il vardır.

Lise Matematik
Rutin Olmayan ProblemlerB
NERGİS DENEMESİ
am
'un
23. Bir lahmacun aşağıdaki şekilde gösterildiği gibi bir bi-
çak darbesiyle en çok iki parçaya, iki bıçak darbesiyle en
çok dört parçaya, üç bıçak darbesiyle en çok yedi parça-
ya ayrılabilir.
N
3
2
6
5
Buna göre, bir lahmacun 8 bıçak darbesiyle en çok
kaç parçaya ayrılabilir?
B) 34
A) 33
C) 35
D) 36
E) 37
10
14
YAYINLARI
3
MITONG ATX MST
MAVIH delle

Lise Matematik
Rutin Olmayan Problemler18. Aşağıda kaba inşaatı tamamlanmış bir siteye takılacak çift sayılı ve tek sayılı pencere camları verilmiştir.
Site ile ilgili olarak aşağıdakiler bilinmektedir.
6 katlıdır.
Her katta 4 daire vardır ve 2 daire kuzey, 2 daire güney yönlüdür.
Kuzey yönlü dairelerde 4 er oda, güney yönlü dairelerde 5 er oda olup her odada 2 şer pencere bulunmaktadır.
Kuzey yönlü dairelerde çift sayılı pencere camı, güney yönlü dairelerde tek sayılı pencere camı kullanılacaktır.
Sitede kullanılacak açılır cam sayısı x, sabit cam sayısı y'dir.
Buna göre, x + y kaçtır?
A) 552
B) 516
C) 496
D) 480
E) 444
.
Lise Matematik
Rutin Olmayan Problemleronuna
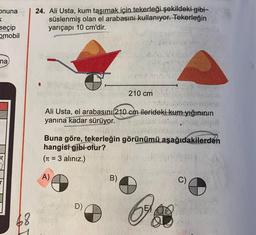
24. Ali Usta, kum taşımak için tekerleği şekildeki gibi-
süslenmiş olan el arabasını kullanıyor. Tekerleğin
yarıçapı 10 cm'dir.
seçip
omobil
na
210 cm
On
Ali Usta, el arabasını 210 cm ilerideki kum yığınının
yanına kadar sürüyor.
ch
Buna göre, tekerleğin görünümü aşağıdakilerden
hangisi gibi olur?
(Tt = 3 alınız.)
A)
B)
C)
D)
EX
68
![o
9. Al Buse ve Can'ın birbirleriyle yapmış oldukları satranç
haçlarıyla ilgili aşağıdakiler bilinmektedir.
aktir.
En az maç yapan Ali'dir ve 10 maç yapmıştır
.
. En çok maç yapan Buse'dir ve 13 maç yapmıştır.
Buna göre, Ali ve Can kendi aralarında kaç maç yap-
mıştır?
nra
lan
A) 2
B)3
C)4
D) 5
E) 6
Aliilo
15
Buse :13]
2281
Cori? 1
5
A
6
20x54x
A
7
C
D
8
C
9](https://media.kunduz.com/media/question/seo/raw/20210315062822665436-2876001_ZxJsrqUex.jpeg?w=256)
Lise Matematik
Rutin Olmayan Problemlero
9. Al Buse ve Can'ın birbirleriyle yapmış oldukları satranç
haçlarıyla ilgili aşağıdakiler bilinmektedir.
aktir.
En az maç yapan Ali'dir ve 10 maç yapmıştır
.
. En çok maç yapan Buse'dir ve 13 maç yapmıştır.
Buna göre, Ali ve Can kendi aralarında kaç maç yap-
mıştır?
nra
lan
A) 2
B)3
C)4
D) 5
E) 6
Aliilo
15
Buse :13]
2281
Cori? 1
5
A
6
20x54x
A
7
C
D
8
C
9
Lise Matematik
Rutin Olmayan Problemlerbir ok
Buna
metr
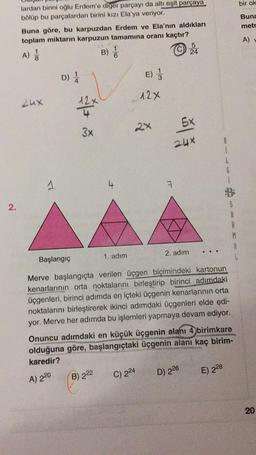
lardan birini oğlu Erdem'e diger parçayı da altı eşit parçaya
bölüp bu parçalardan birini kızı Ela'ya veriyor.
Buna göre, bu karpuzdan Erdem ve Ela'nın aldıkları
toplam miktarın karpuzun tamamına oranı kaçtır?
5
A)
B)
24
A)
D)
E)
12x
Lux
2x
5x
3x
2ux
i
G
1
A
7
2.
S
A
R
M
2. adım
Başlangıç
1. adım
L
Merve başlangıçta verilen üçgen biçimindeki kartonun
kenarlarının orta noktalarını birleştirip birinci adımdaki
üçgenleri, birinci adımda en içteki üçgenin kenarlarının orta
noktalarını birleştirerek ikinci adımdaki üçgenleri elde edi-
yor. Merve her adımda bu işlemleri yapmaya devam ediyor.
Onuncu adımdaki en küçük üçgenin alanı 4 birimkare
olduğuna göre, başlangıçtaki üçgenin alanı kaç birim-
karedir?
C) 224
B) 222
E) 228
D) 226
A) 220
20

Lise Matematik
Rutin Olmayan Problemler1. Özge, gerçel sayılarda çözüm kümesi [0, 4) aralığı
olan bir eşitsizlik oluşturmaya çalışıyor.
Özge'nin bu eşitsizliği oluşturma adımları aşağıda
verilmiştir.
I. adım : 0<x<4
II. adım :-2<x-252
III. adım |x-2152
(x-2), 1
IV. adım :
<
4
2
4
V. adım :
(x-2
22
Buna göre, Özge hangi adımda hata yapmıştır?
B) III.
e IV.
A II.
DW.
EXHata yapmamıştır.
Lise Matematik
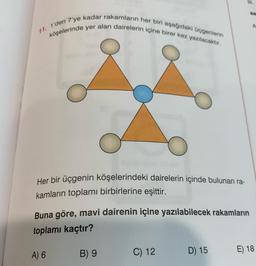
Rutin Olmayan Problemler11. 1'den 7'ye kadar rakamların her biri aşağıdaki üçgenlerin
köşelerinde yer alan dairelerin içine birer kez yazılacaktir.
Her bir üçgenin köşelerindeki dairelerin içinde bulunan ra-
kamların toplamı birbirlerine eşittir.
Buna göre, mavi dairenin içine yazılabilecek rakamların
toplamı kaçtır?
B) 9
A) 6
D) 15
C) 12
E) 18
