Rutin Olmayan Problemler Soruları

N 13. Ceyhun, telefonunda oynadığı bir oyunda kazandığı taşları, A ve B sandıklarına atarak oyun puanı elde edecektir. Ceyhun'un sandıklara taş atması için iki tur hakkı bulunmaktadır. • Birinci turda her iki sandığa da eşit sayıda taş atmıştır. • İkinci turda bir sandığa diğerinden bir tane fazla taş atmıştır. • Her turda her sandığa mutlaka taş atmıştır. EX x sayısı her bir turda sandıklara atılan toplam taş sayısına eşit olmak üzere, her tur sonunda kazanılacak oyun puanını modelleyen fonksiyon aşağıda gösterilmiştir. (3(x+2), Birinci tur sonundaki puan f(x) = x2-3x+2, ikinci tur sonundaki puan | 41 Ceyhun, toplam beş tane taşı iki tur sonunda A ve B sandıklarına atmıştır. Buna göre, Ceyhun'un oyun puanı kaçtır? A) 11 B) 12 C) 14 D) 15 E) 18 IL MATEMATIK

3. Tekrar Testi 16. Şifreli mesajları göndermede ve çözmede kullanılan yöntemlerden biri de fonksiyonlardır. Aşağıda alfabemizdeki her harfe bir sayı karşılık getirilmiştir. Ğ A 1 25 U N 9 17 B Ü 10 H 2 O 26 18 3 1 C 11 Ö V 19 27 4 i ç 12 P Y 20 28 D 5 J 13 R 21 Z 29 E 6 K 14 S 22 F 7 L 15 ş 23 G 8 M 16 T 24 Tablodaki her harfe karşılık gelen sayılar için f(x)=2x +7 fonksiyonu tanımlansın. Bu fonksiyon yardımıyla bir kelimedeki harflere karşılık gelen sayıların bu fonksiyon altındaki görüntüsü o kelimenin şifresi olsun. Örneğin; f(V)=f(27)=2 27+7=61 olduğundan V harfi 61 sayısı ile şifrelenmektedir. Buna göre 63 - 9-35-29-53-39-9-35 şeklinde şifrelenmiş kelime aşağıdakilerden hangisidir? B) YAKINSAK A) YAKINMAK D) YAKLAŞIK C) YAKIŞMAK E) YAKLAŞIM

IIITLIN HIILGICITICO- M de olan ve a aşağıda T CA -2 2 -1, 2) r? Yukarıda analitik düzlemde; M(-1,6), A(2, 1) ve T(-21) noktaları köşeleri olan MAT üçgeni verilmektedir. MAT üçgeninde MA kenarına ait yüksekliği içeren doğrunun x ve y-eksenleri ile sınırlı olan kısmının oluşturduğu alan kaç birimkaredir? A) 121 4. B) 121 C) 11 online la gente D) 121 E) 121

3. Kemal Bey'e doktoru kalbinin daha sağlikli olması için günde en az 25000 adım atması gerektiği tavsiyesinde bulunmuştur. Kemal Bey ortalama adim uzunluğunu ölçüyor ve doktorunun tavsiyesine uyması için en az 15 km yürümesi gerektiğini he- sapiryor Buna göre, Kemal Bey bir adımını ortalama kaç cm olarak ölçmüştür? D) 55 E) 60 C) 50 A) 40 B) 45

ch g 5 26-60 Toli 6. D C ABCD ikizkenar yamuk |AC| = 6 birim Q: y= x l= 6 biva tax be B Yukarıdal, ve lydoğruları ile kurgulanmış ABCD ya- muğunun alanı kaç birimkaredir? A) 9 B) 18 C) 36 D) 72 E) 144 88

cm esil- 28. Bir masa üzerinde bulunan, birim karelerden oluşan 4x4 boyutlanndaki beş oyun tahtası sarı ve maviye boyanarak aşağıdaki görünümler oluşturulmuştur. (1) (2) (3) (5) Numaralandırılmış bu beş Oyun tahtasından her bin, bu masa üzerinde kendi merkezi etrafında aynı ayn döndürüt düğünde yalnızca dördünde aynı görünüm elde edilebiliyor. Buna göre, aynı görünüm elde edilemediği oyun tah- tasinin numarası kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 28 Diğer Sayfaya Geçiniz

Bir böreğin bir yüzünün kızartılması için 18 sn ocak üstündeki tavada kalmak zorundadır. Boyutları şekildeki gibi olan böreklerin her iki yüzü de aynı tava ve bir ocak ile kızartılmak isteniyor. 1 1 1 Şekildeki tava ile aynı anda en çok 3 tane börek kızar- tılabilmektedir. 1 Buna göre, 11 tane börek en az kaç sn'de kızartıla- bilir? 1 1 A) 84 B) 108 C) 132 D) 144 E) 198 2 1 1 1 1 1 1 1 1

Buna göre, başlangıçtaki ses seviyesinin birim turunda alabileceği tam sayı değerleri toplamı kaçtır? C) 97 A) 95 B) 96 D) 98 EM 1 durum: 564 x 17clou our yoni) ugh X683 durumi 1 CX-182 32 = 192 XLSO u 12. Matrix Yazılım Şirketindeki bir bilgisayar yazılımcısı "1" ve "O"ları kullanarak yazılımlar oluşturuyor. On Yazılımda kullanılan "1" ve "O"ların adedi yazılımın uzunluğunu belirlemektedir ve uzunluk U (yazılım) olarak gösterilmektedir. . Yazılımın uzunluğu yazılımcı tarafından belirlenmekte ve aynı sayı yan yana en fazla 11 kez kullanılabilmektedir. Örneğin, T yazılımı 100110 olarak alınır ise U(T) = 6 olur. Buna göre, 100 adet "O" ve sinirsiz sayıda "1" kullanılan oluşturulan T yazılımı için U(T) nin alabileceği en büyü değer kaçtır? E) 124 A) 1200 B) 1210 C) 1211 D) 1221

c) v3 B) V2 A) 1 m - 26. Bir masa üzerinde bulunan, binim karelerden oluşan 4x4 boyutlarındaki beş oyun tahtası sarı ve maviye boyanarak aşağıdaki görünümler oluşturulmuştur. 30. Bir 20 (3) Bu bu (2) (1) ka BU ka A (4) (5) Numaralandırılmış bu beş oyun tahtasından her biri, bu masa üzerinde kendi merkezi etrafında ayn aynı döndürül- düğünde yalnızca dördünde aynı görünüm elde edilebiliyor. Buna göre, aynı görünüm elde edilemediği oyun tah- tasının numarası kaçtır? A) 1 B) 2 C) 3 E) 5 D) 4 28 Diğer Sayfaya Geçiniz

uy. ve her elde ediliyor. 4. 5. 123 sayısına sırasıyla aşağıdaki adımlar gulanarak rakamlarının yerleri değiştiriliyor adımda tekrar üç basamaklı bir sayı elde ediliyor. daki rakamların yerleri değiştirilerek bir sayı 1. adimda, sayinin onlar ve yüzler basamağın- 2. adımda, bir önceki adımda elde edilen sayı- nin birler ve onlar basamağındaki rakamların Bu şekilde devam edilerek, adım numarası tek sayı ise bir önceki adımda elde edilen sayının on- lar ve yüzler, adım numarası çift sayı ise bir önceki adımda elde edilen sayının birler ve onlar basama- ğındaki rakamların yerleri değiştirilerek sayılar elde ediliyor. Buna göre, 75. adım sonunda elde edilen sayı aşağıdakilerden hangisidir? yerleri değiştirilerek bir sayı elde ediliyor. C) 231 A) 321 B) 312 D 213 E) 132

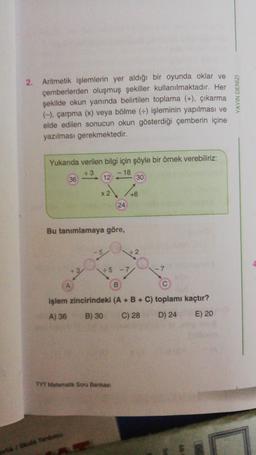
2. Aritmetik işlemlerin yer aldığı bir oyunda oklar ve çemberlerden oluşmuş şekiller kullanılmaktadır. Her şekilde okun yanında belirtilen toplama (+), çıkarma (-), çarpma (x) veya bölme (+) işleminin yapılması ve elde edilen sonucun okun gösterdiği çemberin içine yazılması gerekmektedir. YAYIN DENIZI Yukarıda verilen bilgi için şöyle bir örnek verebiliriz: +3 18 36 12 30 X 2 +6 24 Bu tanımlamaya göre, +5 7 B işlem zincirindeki (A + B + C) toplamı kaçtır? A) 36 B) 30 C) 28 D) 24 E) 20 TYT Matematik Soru Bankası

7. L Rakamları birbirinden farklı olan dört basamaklı abcd doğal sayısı için (a+b) (c+d) çarpımından elde edilen sayıya ra- kamsal çarpım denir. yayıl llar Buna göre, rakamsal çarpımı 18 olan dört basamaklı kaç farklı sayı vardır? A) 32 B) 34 C) 36 SD) 38 E) 40

16k 246 6. Mavi, kimızı ve yeşil renkli, bir miktar şişirilmiş üç balon hakkında aşağıdaki bilgiler biliniyor. Mavi balondaki hava miktarı, kırmızı balondaki hava miktarının ünden 10 mm fazladır. 4 . Kırmızı balondaki hava miktarı, yeşil balondaki hava 3 miktarının sinden 8 mm fazladır. 2 Bu üç balon içinden hava geçebilen bir bağlantı borusuyla birbirine bağlanmış ve balonlardaki hava miktarları eşitlen- mistir. Son durumda mavi balonun içindeki hava 44 mm azal- dığına göre, yeşil balonun içindeki hava kaç mmart- mıştır? A) 40 B) 42 C) 44 D) 46 E) 48 $(42X +8) +10 -uu = 12

LOGARITMA ÜNİTE 3 1. de ABD'li sismolog Richter günümüzde kullanılan "Richter ölçeği"ni bulmuştur. Bu ölçek çeşitli bölgelere yerleştirilen sismogratlar yardımıyla sarsıntının merkezi, etki alanı, bü- yüklüğü, şiddeti ve açığa çıkardığı enerjinin matematiksel büyüklüğüdür. Bir depremin şidddeti 10'un kuvvetleri ile, büyüklüğü şiddetin onluk logaritması ile ifade edilir. 1939 Erzincan Depremi 2003 Bingöl Depremi 7,9 5,9 Büyüklük Buna göre, 1939 yılında Erzincan'da meydana gelen depremin şiddeti, 2003 yılında Bingöl'de meydana ge- len depremin şiddetihin yaklaşık kaç katı olabilir? B) 20 A) 2 C) 40 E) 100 D) 50 10.7,9 10.5.9

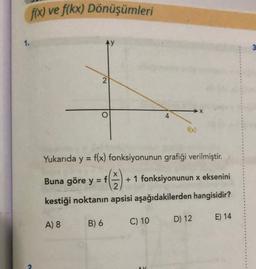
f(x) ve f(kx) Dönüşümleri 1. 2 →X O f(x) Yukarıda y = f(x) fonksiyonunun grafiği verilmiştir. = X = Buna göre y = = f + 1 fonksiyonunun x eksenini 2 kestiği noktanın apsisi aşağıdakilerden hangisidir? D) 12 E) 14 A) 8 B) 6 C) 10

A TEMEL MATEMATİK TESTI 17 200 Litre Y.SIVISI 80 Litre İçme suyu Depo - 1 Depo - 11 Depo - I'deki içme suyunun içinde % 30 oranında zararli X maddesine rastlanmıştır. Zararlı maddeyi içme suyuna çevirmek için eklenen bir miktar Y SI- visi, X sivisinin % 50'sini etkisiz hâle getirip içme suyuna çeviriyor. Son durumda birinci depoda % 5 oranında X SIVISI kaldığına göre ikinci depoda kaç litre Y SIVISI kalmıştır? O B) 50 C) 78 D) 150 E) 162