Trigonometri Soruları

Lise Matematik
TrigonometriTRIGONOMETRI
2cos7
ilerden
Sx
ecosx
5.
3-
8+ sin²x
3 COSX
ifadesinin en sade şekli aşağıdakilerden
hangisidir?
A) COSX
Bị cosx
D) 2-sinx E) 1+ sinx
C) 3 – cosx
1-2sinx= m ve 1+2cosx=n
olduğuna göre, m ile n arasındaki bağıntı
aşağıdakilerden hangisidir?
A) n²+ m²-2m-2n = 2
B) n²+ m²-2m + 2n = 2
C) n²-m²-2m-2n = 2
D) n²+m²+2m-2n=2
E) m²-n²+2m-2n=2
ÖGRENIT
Trigonom
sin²x
. 00=
• tanx =
secx=
cosecx
1+ tan
1+ cot
• lanx =
![eye-
beccel
acağ
251-
ödev:
11. Zühre Öğretmen'in, öğrencisi Egemen'den istediği
. Sadece şekil çizerek Temel Oranti - Tales (AA)
benzerlik teoremlerini, orta noktalar kullanarak iki
farklı yamuk üzerinde ve kendine özgü biçimde
yorumla.
A
Egemen'in hazırladığı ödev aşağıdaki gibidir.
991/Egemen
B
E
a
D
K
YORUM:
ABCD yamuğunda; [AB] // [CD], [AB] = a, |CD| = c,
E ve F noktaları bulundukları kenarların orta nokta-
lan; [AC] ve [BD] köşegen olmak üzere,
1.
C
a
E
E
3. |EK| = dir.
4. |KF|= dir.
1. [EF] // [AB] dir.
2 |AK|=|KC| dir.
C
✓
C
ise |AE|-|EC|
C
ise [DE] // [BC]/
ADE - ABC
||DE| = 2
F
B
www.deltakitap.com
11.
E
A
D
K
C
O
L
a
1. |EK|LF| dir.
2. JELI=KFI dir.
3. KLI=
a+c
ato dir.
D) II de 3.
DENEME SINAVI 1-B
C
F
B
4. |EF|= dir.
Ödevi alan Zühre Öğretmen: "Güzel bir çalışma ol-
muş ancak bir tek hata yapmışsın, onu da düzeltip
getir." diyor.
Buna göre, Egemen'in yanlış yaptığı yorum, aşa-
ğıdakilerden hangisidir?
Alt de 2
B) II de 1.
C) I de 4.
E) Il de 4.](https://media.kunduz.com/media/question/seo/raw/20220911161330298192-4099060.jpg?w=256)
Lise Matematik
Trigonometrieye-
beccel
acağ
251-
ödev:
11. Zühre Öğretmen'in, öğrencisi Egemen'den istediği
. Sadece şekil çizerek Temel Oranti - Tales (AA)
benzerlik teoremlerini, orta noktalar kullanarak iki
farklı yamuk üzerinde ve kendine özgü biçimde
yorumla.
A
Egemen'in hazırladığı ödev aşağıdaki gibidir.
991/Egemen
B
E
a
D
K
YORUM:
ABCD yamuğunda; [AB] // [CD], [AB] = a, |CD| = c,
E ve F noktaları bulundukları kenarların orta nokta-
lan; [AC] ve [BD] köşegen olmak üzere,
1.
C
a
E
E
3. |EK| = dir.
4. |KF|= dir.
1. [EF] // [AB] dir.
2 |AK|=|KC| dir.
C
✓
C
ise |AE|-|EC|
C
ise [DE] // [BC]/
ADE - ABC
||DE| = 2
F
B
www.deltakitap.com
11.
E
A
D
K
C
O
L
a
1. |EK|LF| dir.
2. JELI=KFI dir.
3. KLI=
a+c
ato dir.
D) II de 3.
DENEME SINAVI 1-B
C
F
B
4. |EF|= dir.
Ödevi alan Zühre Öğretmen: "Güzel bir çalışma ol-
muş ancak bir tek hata yapmışsın, onu da düzeltip
getir." diyor.
Buna göre, Egemen'in yanlış yaptığı yorum, aşa-
ğıdakilerden hangisidir?
Alt de 2
B) II de 1.
C) I de 4.
E) Il de 4.

Lise Matematik
Trigonometri10. Aşağıda gösterilen ikişer renkli AB, CD ve EF çubuklarinin
uzunlukları sırasıyla 12 sinx, a ve b'dir.
B
a
E
A) 2
C
b
cos y
B) 3
5
Utku'nun bu çubukları birleştirerek yaptığı üçgenin bir kıs-
mı aşağıda verilen Şekil 1'deki gibidir.
Şekil 1
Şekil 2
^^
y
F
oranı kaçtır?
Şekil 2'de ise bu üçgende x açısının olduğu köşeden karşı
kenara çizilen dikmenin bir kısmı gösterilmiştir.
Buna göre,
C) 4
Test
D
D) 6
VTT
12
YT
Test
12. Aşa
Uc
re
ya
U
1
r

Lise Matematik
Trigonometrin
31. Meteoroloji uzmanları bulut yüksekliklerini ölçmek için
silometre adı verilen bir alet kullanırlar. Silometre
aşağıdaki şekilde gösterildiği gibi ışık projektörü ve ışık
dedektörü olmak üzere iki kısımdan oluşur. Işık projektörü
bulut tabanına ışık gönderirken, ışık dedektörü ışınları
yakalayabilmek için bulutu tarar.
Işık
dedektörü
X
Yer Düzlemi
1200.
27
1200
Yukarıdaki şekilde işık projektörü ile ışık dedektörü
arasındaki mesafe 1200 m'dir.
D) 2356
Işık dedektörünün ışıkları yakalama açısı 63°
olduğuna göre, bulutların yerden yüksekliği (h)
yaklaşık olarak kaç metredir?
(tan 63° 1,96)
A) 2350
h
B) 2352
DENEME-10
186
Işık projektörü
go
us
100 50 25
E) 2358
C) 2354
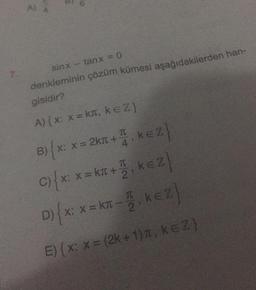
Lise Matematik
Trigonometri7.
sinx
tanx =0
denkleminin çözüm kümesi aşağıdakilerden han-
gisidir?
A) { x: x = kπ, KEZ}
B) {x: x
B) x: x = 2km +-
I
4
},
KEZ}
T
C) { x: x = km + ₁ k€ Z}
2
D) { x: x = KT-1₁ KEZ}
2
E) { x: x = (2k + 1), k=Z}

Lise Matematik
Trigonometri2
13
a ER* olmak üzere, birim çember üzerinde verilen A(-a, b)
noktasına karşılık gelen açının ölçüsü aşağıdakilerden han-
gisi olabilir?
16 IT 2TT
2TT JED
4л
C) ATT
A) 56
5
4017
28/10 1814
938 9
9
B)
9²
D) -25 E) - 9
3
5
251 4
+ b

Lise Matematik
TrigonometriNT VE KOSEKANT FONKSİYONLARI
2. 0<a<
tana-cot²a=
olduğuna göre, seca kaçtır?
B) / 1
C) 3/3/20
54
olmak üzere,
A) 5/20
oca < 80
COS
D) 2 E) 3
5. Tanımlı oldu
1+tar
19
sec
ifadesinin
A)-2
1+ SI
1
Cos
F
T

Lise Matematik
Trigonometri11.
cosx–sinx=m
denkleminin çözüm kümesi boş küme olmadığına
göre, m nin en geniş çözüm aralığı aşağıdakilerden
12 hangisidir?
12.
A) |m|≤2√2
D) |m|≤√2
542=1
go
B) |m|≤2
dost+ou =21/2
645 an
E) |m|≤1
sux tco101
C) |m|<√3
![L
6
B
10.
M
Tonimaire 1≤9≤5
as
10, 1, 2, 3, 415
A = sin²a - 2sina
olduğuna göre, A'nın en geniş değer aralığı aşağıdakiler-`
den hangisidir?
A) [-3,1]
B) [-2,2]
c) (-1,3]
D) [0,4]
Sina = 2sma+A.
E) [1,5]](https://media.kunduz.com/media/question/seo/raw/20220907185517561597-2856774.jpeg?w=256)
Lise Matematik
TrigonometriL
6
B
10.
M
Tonimaire 1≤9≤5
as
10, 1, 2, 3, 415
A = sin²a - 2sina
olduğuna göre, A'nın en geniş değer aralığı aşağıdakiler-`
den hangisidir?
A) [-3,1]
B) [-2,2]
c) (-1,3]
D) [0,4]
Sina = 2sma+A.
E) [1,5]

Lise Matematik
TrigonometriFASİKÜL
TRIGONOMETRI Kavrama Testi: 01
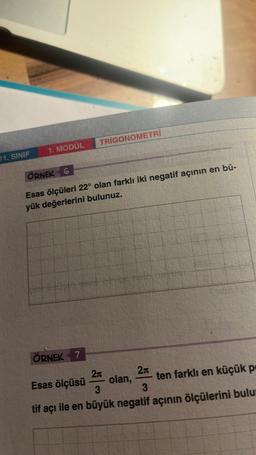
7.
2
1 + sin50°
2 sin25° + cos25°
ifadesinin eşiti aşağıdakilerden hangisidir?
A) -cos25°
2+2545-
suso
D) sin25°
1-
8u25
sin25°
Sugos + sus
B) cos25°
C) -sin25°
E) cos65°-sin65°
10.
2+2suzsicos25+ sussis
Sus
Lise Matematik
Trigonometri11. SINIF
1. MODÜL
ÖRNEK G
Esas ölçüleri 22° olan farklı iki negatif açının en bü-
yük değerlerini bulunuz.
ÖRNEK 7
TRIGONOMETRI
2
2a
Esas ölçüsü
3
tif açı ile en büyük negatif açının ölçülerini bulu
S
olan,
ten farklı en küçük p

Lise Matematik
TrigonometriÖRNEK 8
m(A) = 52° 28' 13"
m(B) = = 17° 36' 24"
veg
olmak üzere, aşağıdaki
a) m(A) +m(B)
hreybay as - 2086 cop snu
ÖRNEK 9
a)
70 04 37
m(A)
2
94115
52
17
44
Leupló nimps
nebnianio navbeA
ifadelerin eşitini bulunuz.
b) m(A)-m(B)
°008 (1
m(A) = 19° 22' 30", m(B) = 27° 13' 21"
olmak üzere, aşağıdaki ifadelerin eşitini bulunuz.
b)
"OTS (
m(B
3
9'4 277
22
132
ha
O

Lise Matematik
TrigonometriE
A)
tana
2
To
Ja
D)
D
B
C_y=1
Analitik düzlemde O merkezli birim çember ile y=1 doğrulan
verilmiştir.
A
Buna göre, ECB üçgeninin alanı aşağıdakilerden han-
gisine eşittir?
cota-cosa
2
X
cota
2
m(COA)=c
E)
1-tana
2
C)
tana + cota
2
Con

Lise Matematik
Trigonometri8.
ifadesinin en sade biçimi
gisidir?
A) 1
sinx + cosx +
B) sino
D) cosect
E)-sec0
sinx + cosx
+
COSX
E) sin²x - cos²x
C) cose
sina-sine cosa-cose
cosa + cose sina + sine
sinx – 1
Şekildeki kartonun alanının trigonometrik ifa-
desi aşağıdakilerden hangisine eşittir?
A) 1 – sinx − coSX
B) (sinx + cosx)
C) 2cosx-2
D) 2sinx - cosx
sinx
COSX
![Örnek
ABC dik üçgen, [AC] [AB], |AC| =8 cm, |AD|=4 cm
|DB|=2 cm, m(DCB) =a dir.
A
C
a
A
Buna göre, tanc ifadesinin değeri kaçtır?
3
4
Örnek
ABCD dörtgen, |AD|=3 cm, |DC| =4 cm,
|AB| = 2√5 cm ve m(DAB)= a dir.
D
D 2 B](https://media.kunduz.com/media/question/seo/raw/20220907090504150634-4496166.jpg?w=256)
Lise Matematik
TrigonometriÖrnek
ABC dik üçgen, [AC] [AB], |AC| =8 cm, |AD|=4 cm
|DB|=2 cm, m(DCB) =a dir.
A
C
a
A
Buna göre, tanc ifadesinin değeri kaçtır?
3
4
Örnek
ABCD dörtgen, |AD|=3 cm, |DC| =4 cm,
|AB| = 2√5 cm ve m(DAB)= a dir.
D
D 2 B
Lise Matematik
Trigonometri(a-p)
Cont
Johb
MIN
A)
Duvar
? uygulama 15
4
2,5 m
Yer düzlemi
1
ğeri kaçtır? (tana =-
α
B)
1
0,9 m
91310
A
07
07+0
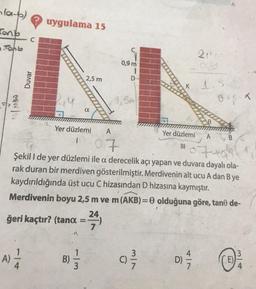
Şekil I de yer düzlemi ile a derecelik açı yapan ve duvara dayalı ola-
rak duran bir merdiven gösterilmiştir. Merdivenin alt ucu A dan B ye
kaydırıldığında üst ucu C hizasından D hizasına kaymıştır.
Merdivenin boyu 2,5 m ve m (AKB)=0 olduğuna göre, tane de-
24.
5M
D
3/1
Yer düzlemi
|||
2144
D) 17/12
1.5
0 + 8-K
A B
(E)
3/4
