Trigonometrik Denklemler Soruları
![Aşağıdaki koordinat düzlemi üzerinde birim
çember ve (OA çizilmiştir.
y
men
C
D
n
mun
o
B
[AB] 1 (OB), (CD) 1(OC) olmak üzere, AB ve
CD uzunlukları şekil üzerinde gösterilmiştir
.
Buna göre, Plin) noktasının koordinatları
çarpımı kaçtır?
a) 2 B
3
)
D)
V
E
C)
V6
D)
A
5](https://media.kunduz.com/media/question/seo/raw/20220417141933745353-429186_B53Ru5Zkn.jpg?w=256)
Lise Matematik
Trigonometrik DenklemlerAşağıdaki koordinat düzlemi üzerinde birim
çember ve (OA çizilmiştir.
y
men
C
D
n
mun
o
B
[AB] 1 (OB), (CD) 1(OC) olmak üzere, AB ve
CD uzunlukları şekil üzerinde gösterilmiştir
.
Buna göre, Plin) noktasının koordinatları
çarpımı kaçtır?
a) 2 B
3
)
D)
V
E
C)
V6
D)
A
5
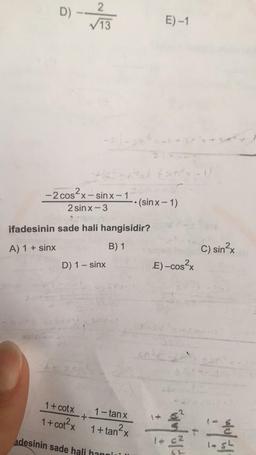
Lise Matematik
Trigonometrik DenklemlerD)
2
✓13
E)-1
---
G
Esin - 1
-2 cos?x-sinx-1
2 sin x-3
.
• (sin x-1)
ifadesinin sade hali hangisidir?
A) 1 + sinx
B) 1
C) sin?
2x
D) 1 - sinx
E) -cos2x
1 + cotx
1 + cot²x
1 -tan x
+
1 + tan²x
I to
nh
-
adesinin sade hali hangin
N
+ 2
last
![At
B
it lood
Yukarıdaki şekilde 41 metre yüksekliginde bir banka
binasının zemininde ve tepesinde bulunan iki kameranın
bazı konumlarındaki yerle oluşan görüş açılar verilmişir.
cos 34 -0,82 ve sin 120,2
olduğuna göre, PAF reklaminin olduğu tabelanın AB
yüksekliği kaç metredir?
C) 4,8
D) 4
E) 3,6
-la a to
31.
A) 6,4
wy
AT
w
11-10
B
Tn
29.
Bo?
sushi
Pergh
sing
Snovikdeki ön y
olan kâğit B kös-
katlandığındaş
B
Palme Yavin
P
a
AL
O
B
B
4 +44
Yukarıdaki birim çemberde APA' üçgeninin alanını
aşağıdaki iki yolla çözen Ulaş öğretmen daha sonra
bulduğu sonuçları birbirine eşitliyor.
Elde ediler
uçları D ve
açıldığınd
ölçülmüş
I. Yol: |AP| ve A'P| uzunlukların a türünden bulup
m(APA) = 90° yi kullanarak.
II. Yol: Önce |OP| yarıçapını çizip P noktasından
[AA'] çapına inen yüksekliği ile |AA'l uzunluğunu
kullanarak
Buna göre, Ulaş öğretmen aşağıda verilen
özdeşliklerden hangisini ispatlamış olur?
Şek
der
=
+
A) sin2a = 2sina . cosa B) cos2a = cos?a - sin?a
2 tan a
C) tan2a =
D) sin?a + cos2a = 1
1-tan² a
E) 1 + tanda = seca
A)
(2thces) (2-200
Z le-klash= 25982
ull-cokl=](https://media.kunduz.com/media/question/seo/raw/20220422205505744513-502511_szBx9KVpd.jpg?w=256)
Lise Matematik
Trigonometrik DenklemlerAt
B
it lood
Yukarıdaki şekilde 41 metre yüksekliginde bir banka
binasının zemininde ve tepesinde bulunan iki kameranın
bazı konumlarındaki yerle oluşan görüş açılar verilmişir.
cos 34 -0,82 ve sin 120,2
olduğuna göre, PAF reklaminin olduğu tabelanın AB
yüksekliği kaç metredir?
C) 4,8
D) 4
E) 3,6
-la a to
31.
A) 6,4
wy
AT
w
11-10
B
Tn
29.
Bo?
sushi
Pergh
sing
Snovikdeki ön y
olan kâğit B kös-
katlandığındaş
B
Palme Yavin
P
a
AL
O
B
B
4 +44
Yukarıdaki birim çemberde APA' üçgeninin alanını
aşağıdaki iki yolla çözen Ulaş öğretmen daha sonra
bulduğu sonuçları birbirine eşitliyor.
Elde ediler
uçları D ve
açıldığınd
ölçülmüş
I. Yol: |AP| ve A'P| uzunlukların a türünden bulup
m(APA) = 90° yi kullanarak.
II. Yol: Önce |OP| yarıçapını çizip P noktasından
[AA'] çapına inen yüksekliği ile |AA'l uzunluğunu
kullanarak
Buna göre, Ulaş öğretmen aşağıda verilen
özdeşliklerden hangisini ispatlamış olur?
Şek
der
=
+
A) sin2a = 2sina . cosa B) cos2a = cos?a - sin?a
2 tan a
C) tan2a =
D) sin?a + cos2a = 1
1-tan² a
E) 1 + tanda = seca
A)
(2thces) (2-200
Z le-klash= 25982
ull-cokl=
![3t.
33.
B.
w
A
H
Ta
C
ABCO dikdörtgeninin B köşesi O merkezli birim ya-
rim çember üzerindedir.
Bi
ki
[BC] ve [AO] üç eşit parçaya ayrılmıştır.
A
A
(
m(BOC)=a olduğuna göre, tarali bölgenin alani-
nin a türünden eşiti aşağıdakilerden hangisidir?
sin 2a
A) sina.cosa
B)
12
sin a. cosa
C)
3
cota
D)
3
E) tanza
sind cost
1, sind
OS
3
-
SR
23](https://media.kunduz.com/media/question/seo/raw/20220422085251762802-526480_OOmI4Qdwt.jpeg?w=256)
Lise Matematik
Trigonometrik Denklemler3t.
33.
B.
w
A
H
Ta
C
ABCO dikdörtgeninin B köşesi O merkezli birim ya-
rim çember üzerindedir.
Bi
ki
[BC] ve [AO] üç eşit parçaya ayrılmıştır.
A
A
(
m(BOC)=a olduğuna göre, tarali bölgenin alani-
nin a türünden eşiti aşağıdakilerden hangisidir?
sin 2a
A) sina.cosa
B)
12
sin a. cosa
C)
3
cota
D)
3
E) tanza
sind cost
1, sind
OS
3
-
SR
23
![ABCD dortgeninde CDI AB IAC) aç ortay IDCI = 4 cm.
JACI 6 cm ve ABL 9 cm dir
M(ABC) - olduğuna göre, cosa degeri kaçtır?
D) 2
3
E)
Art. 2
2 k-2 26522
3 cosa
4 ~36+81-87.4.2
ky
tammat yayincilik
34
32.
D
8
C
%
6
6
4
A
A
10
B
ABCD dörtgeninde [AB] // [CD], [AD] - [CD]
JADI = 6 cm ve ABI = 10 cm dir.
ABC üçgeninin AC doğrusuna göre simetriği çizildiğinde D
noktası BC kenarı üzerinde olmaktadır.
Buna göre, ABCD dörtgeninin alanı kaç cm² dir?
A) 24
B) 36
C) 30
D) 32
ammat
E) 40
yayanCIER
28](https://media.kunduz.com/media/question/seo/raw/20220417193019346383-328318_13rVHeyAl.jpg?w=256)
Lise Matematik
Trigonometrik DenklemlerABCD dortgeninde CDI AB IAC) aç ortay IDCI = 4 cm.
JACI 6 cm ve ABL 9 cm dir
M(ABC) - olduğuna göre, cosa degeri kaçtır?
D) 2
3
E)
Art. 2
2 k-2 26522
3 cosa
4 ~36+81-87.4.2
ky
tammat yayincilik
34
32.
D
8
C
%
6
6
4
A
A
10
B
ABCD dörtgeninde [AB] // [CD], [AD] - [CD]
JADI = 6 cm ve ABI = 10 cm dir.
ABC üçgeninin AC doğrusuna göre simetriği çizildiğinde D
noktası BC kenarı üzerinde olmaktadır.
Buna göre, ABCD dörtgeninin alanı kaç cm² dir?
A) 24
B) 36
C) 30
D) 32
ammat
E) 40
yayanCIER
28
![- ÖRNEK (16
en
Ay
6
239
C
[PH] LOy
m(COP)=50
X
50°
A
1
sin 230
P
H
250
D
O noktası birim çemberin merkezi olduğuna göre,
|DH| kaç birimdir?
A) 1 - cos230°
cos230°– sin230°
B) 1+ cos230°
D) 1+sin230° °
-
of ca
E) 1 tsin230°](https://media.kunduz.com/media/question/seo/raw/20220416110652249924-429347_tjcRQLR9b.jpg?w=256)
Lise Matematik
Trigonometrik Denklemler- ÖRNEK (16
en
Ay
6
239
C
[PH] LOy
m(COP)=50
X
50°
A
1
sin 230
P
H
250
D
O noktası birim çemberin merkezi olduğuna göre,
|DH| kaç birimdir?
A) 1 - cos230°
cos230°– sin230°
B) 1+ cos230°
D) 1+sin230° °
-
of ca
E) 1 tsin230°
Lise Matematik
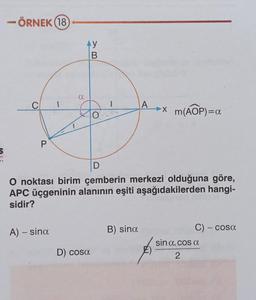
Trigonometrik Denklemler- ÖRNEK (18
4 y
B
a
C
1
A »X
>
m(AOP)=a
0
P
5
am
D
O noktası birim çemberin merkezi olduğuna göre,
APC üçgeninin alanının eşiti aşağıdakilerden hangi-
sidir?
A) – sina
B) sina
-
C) - cosa
sin a. cos a
D) cosa
2
Lise Matematik
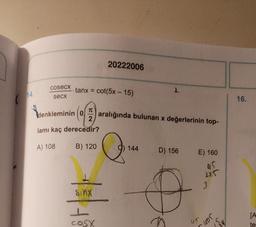
Trigonometrik Denklemler20222006
cosecx
tanx = cot(5x - 15)
1
14.
secx
16.
Vdenkle
TO
denkleminin (0)
2
lamı kaç derecedir?
(9)
aralığında bulunan x değerlerinin top-
A) 108
B) 120
Q
144
D) 156
E) 160
US
1
225
3
sinx
L
COSX
[A
Jon
ur
su
te
Lise Matematik
Trigonometrik DenklemlerB) 573
C) 8
D) 10
E) 10/3
w
X
Singo
bis
4
Schne
-
lo
Tasso
2M
to
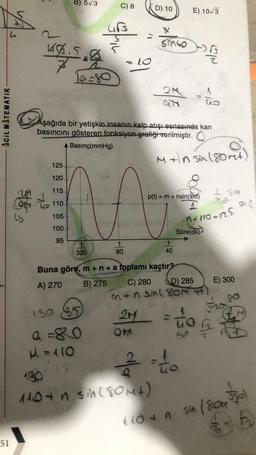
ACIL MATEMATIK
Aşağıda bir yetişkin insanın kalp atışı esnasında kan
basıncını gösteren fonksiyon grafiği verilmiştir. O
Basınç(mmHg)
Miln sin 180rt)
125
120
115
p(t)
= m + nsin(at)
Stos
a to
1 so
sh
Go 110
105
n+110-125
100
Süre(dk)
95
1
80
320
40
E) 300
Buna göre, m+n + a toplamı kaçtır?
A) 270 B) 275 C) 280
D) 285
men sin(80M 7
80
180
20
ton
OM
S
7
a=80
M = 110
190 è to
110 tn sin(80ut)
A
" lot n. sin 1800 570)
a
En
51

Lise Matematik
Trigonometrik DenklemlerOrta
Kolay-One
ortako
TRIGONOMETRİ-
Sınavda
Bu Tarz
Sorar!
3. Aşağıda, O merkezli çeyrek birim çember gösterilmiştir.
D
Uygun
5.
fonksi
E
B(0, 1)
A(1,0)
B(0, 1)
DA LOA
EBI OB
m(DOA) = 72
O, E, D doğrusa
Buna
1
A)
72°
X
A(1,0)
Dan
olduğuna göre, boyalı bölgenin alanı kaç birimkaredir
rosy
A) sin36º. cos 18°
B)
sin 36º.cos 18°
C) tan36° • tan72°
D)
D)
tan 36º. tan 72

Lise Matematik
Trigonometrik Denklemler9. a, B ve e dar açılar olmak üzere,
sin (n – a) + sin(3x + 3) = 0
B
– a
2
eşitliği veriliyor.
Buna göre,
1. sin(a + B + 0) = cos
II. Cos (0 - 3) = sin(a + 0)
III. tan(O+B) = cot(0 - a)
-
+
ifadelerinden hangileri doğrudur?
A) Yalnız!
B) I ve II
C) II ve III
D) I ve III
E) I, II ve III

Lise Matematik
Trigonometrik Denklemler31. Hazırlayacağı deneme için aşağıdaki soruyu yazan Ozge,
kontrol aşamasında kontrolü yapan Ahmet Bey'den sorunun
hatalı olduğu uyansını alıyor.
DENEME 3A
7) 0<x<
olmak üzere,
COSX
4 sinx 3 COSX
tanx
O O O O O
eşitliği veriliyor.
Buna göre, cotx değeri kaçtır?
Özge ve Ahmet Bey arasında aşağıdaki konuşmalar geçiyor:
Özge: Ahmet Bey, sorunun neden hatalı olduğunu
düşünüyorsunuz?
Ahmet Bey: Verilen değerlere göre cevabı şıklarda
bulamıyorum. Ancak sinx'in kat sayısı 4
yerine 7 verilirse cevabı buluyorum.
Özge: Haklısın Ahmet Hocam, 4'ü 7 yapayım.
Teşekkürler.
Season
Buna göre, sorunun hatasız hâlinde bulunan x açısı ile
hatalı hâlinde bulunan x açısı arasındaki farkın tanjant
değeri aşağıdakilerden hangisi olabilir?
1
1
B)
C)
E)
5
4
3
A)
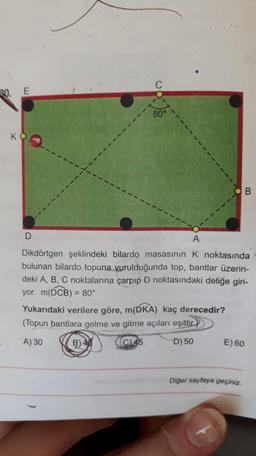
Lise Matematik
Trigonometrik Denklemler30. E
80°
K
OB
D
A
Dikdörtgen şeklindeki bilardo masasının K noktasında
bulunan bilardo topuna vurulduğunda top, bantlar üzerin-
deki A, B, C noktalarına çarpıp D noktasındaki deliğe giri-
yor. m(DCB) = 80
Yukarıdaki verilere göre, m(DKA) kaç derecedir?
(Topun bantlara gelme ve gitme açıları eşittir.)
A) 30 B) 40 C)45 D) 50
E) 60
Diğer sayfaya geçiniz.
![.
ABCD dörtgen
D
m(AEF) = 30°
m(ABC) = 70°
E
300
700 B
A
ABCD dörtgeni biçimindeki kağıt (AE) boyunca
katlandığında AB ve AD kenarları, (CF] bo-
yunca katlandığında BC ve CD kenarları aynı
doğru üzerine gelmektedir.
Buna göre, m(ADC) = u kaç derecedir?
A) 110 B) 120 C) 130 D) 140 E) 150](https://media.kunduz.com/media/question/seo/raw/20220410211804504429-878391_XRre5vxAb.jpg?w=256)
Lise Matematik
Trigonometrik Denklemler.
ABCD dörtgen
D
m(AEF) = 30°
m(ABC) = 70°
E
300
700 B
A
ABCD dörtgeni biçimindeki kağıt (AE) boyunca
katlandığında AB ve AD kenarları, (CF] bo-
yunca katlandığında BC ve CD kenarları aynı
doğru üzerine gelmektedir.
Buna göre, m(ADC) = u kaç derecedir?
A) 110 B) 120 C) 130 D) 140 E) 150
![19
X
100
siobo
385=77
x=5
(30.
sin (10+
()
33.
.
sin (60° + a)
2
2sin( 15° + sin 75°-
4
eşitliğini sağlayan en küçük pozitif a açısı kaç de-
recedir?
ista
A) 15 B) 30 C) 45 D) 60 1 E) 90
2.1 %
sinbo.cosa + sinx.coubo
a co sotsia
isin 15, cosa
X
cosa + Sir
4
sino 10000
2
31.
=
f(x) = sinx ve g(x) = cos2x
g(x) - 1 = f(x)
denkleminin [0, ve] aralığındaki köklerinin toplano
aşağıdakilerden hangisidir?
-45
+180
225
TS
JT
-Aal
B)
ht
D)
E)
70
6
2](https://media.kunduz.com/media/question/seo/raw/20220412160819681513-371645_7msdBAwSs.jpg?w=256)
Lise Matematik
Trigonometrik Denklemler19
X
100
siobo
385=77
x=5
(30.
sin (10+
()
33.
.
sin (60° + a)
2
2sin( 15° + sin 75°-
4
eşitliğini sağlayan en küçük pozitif a açısı kaç de-
recedir?
ista
A) 15 B) 30 C) 45 D) 60 1 E) 90
2.1 %
sinbo.cosa + sinx.coubo
a co sotsia
isin 15, cosa
X
cosa + Sir
4
sino 10000
2
31.
=
f(x) = sinx ve g(x) = cos2x
g(x) - 1 = f(x)
denkleminin [0, ve] aralığındaki köklerinin toplano
aşağıdakilerden hangisidir?
-45
+180
225
TS
JT
-Aal
B)
ht
D)
E)
70
6
2

Lise Matematik
Trigonometrik Denklemlertaxy
9.
5sinx + 12cosx = 13
olduğuna göre, 6 sinx + 4 cosx ifadesinin eşiti kaçtı
A) 8
B) 7
C) 6
D) 5
E) 4
72k
324
10. 5sinºx - 2sinx - cosx - 3cos2x = 0
denklemini sağlayan en küçük pozitif x değeri aşağı
dia
