Türev Alma Soruları

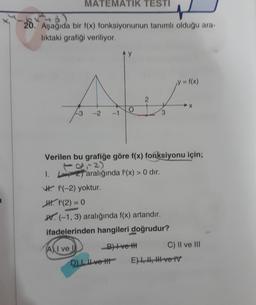
MATEMATIK TESTI I 20. Asagida bir f(x) fonksiyonunun tanımlı olduğu ara- liktaki grafiği veriliyor. 1 1(x) f(x Ae 2 -2 3 Verilen bu grafiğe göre f(x) fonksiyonu için; I. 2) aralığında f'(x) > 0 dir. W. f(-2) yoktur. H. f'(2) = 0 W. (-1,3) aralığında f(x) artandır. ifadelerinden hangileri doğrudur? All ve B)+ve the C) II ve III DI Il ve It E) 4, H, HI-ve IV

Bir hastanın kan basıncını düşürmek için 1 40 {x: İlacın dozu (mg), , f(x) x2.(30 - x) f: Kan basinci 7 biçiminde tanımlanıyor. Buna göre kan basıncının minimum olması için has- taya enjekte edilecek ilacın dozu kaç mg olmalıdır? C) 20 E) 30 B) 15 A) 12 D) 25

le 23. f: R - {0} → R olmak üzere, 2x2-1 f(x) = X fonksiyonu veriliyor. Buna göre, f fonksiyonu ile ilgili, 1. Minimum değeri 2'dir. II. (0,00) aralığında azalandır. III. (-0, 0) aralığında artandır. ifadelerinden hangileri doğrudur? 2 O A) Yalnız! B) Yalnız III C) I ve II D) I ve III E) II ve III 1

SORU - 5 ORİJİNAL MATEMATİK f ve g gerçel sayılar kümesi üzerinde tanımlı ve türev. lenebilen iki fonksiyon olmak üzere f(x) = gº(x).x2 ve g(2) =g'(2) = 2 olduğuna göre f'(2) değeri kaçtır? f'(x) =3 gul.g1.x+2X. f/2) = 12.2.4+4,8

Soru - 61 AYT 2018 Bir internet şirketi en fazla 1000 müşteriye hizmet verebil- mekte ve aylık internet ücretini 40 TL olarak belirlediğinde bu sayıya ulaşabilmektedir. Bu şirket aylik internet ücretin- de yaptığı her 5 TL'lik artış sonrasında müşteri sayısında 50 azalma olduğunu gözlemlemiştir. Bu şirket, aylik internet ücretinden elde edeceği toplam gelirin en fazla olması için aylık internet ücretini kaç TL olarak belirlemelidir? A) 55 B) 60 C) 65 D) 70 E) 75 Çözüm hotsx (1000-sox) 2x I S. (1000-sox) t-soillotsx] X- 5000 2500-2000 2x+13 - 2rox -SooxtZoo C: D

8 . f(x) = x3 – X eğrisi x 11. - 2 .- I. y = 2x + 1 II. y = 2x + 2 III. y = 11x +6 doğrularından hangilerine teğettir Şekild da te C) Yalnız A) Yalnız! B) Yalnız II Buna E) I, II ve III D) II ve III kaç A) 4

28. Eşitsizliklerde temizlik | Murat Çelikkaya 0'dan farklı bir a reel sayısı için x² + ax - - 2 = 0 a? a denkleminin kökleri xı ve x2'dir. Buna göre, x1 + x2* toplamının alabileceği en kü- çük değer kaçtır? A) 3+ √2 B) 3+212 C) 3+3 D) 4+2 0 4 4+2√2

Türev Alma Kuralları - Bileşke Fonksiyonun Türe Fonksiyonlarda Türevi [f(U)]' = f'(U). U Soru – 24 f(5x – 3) = x3 + 3x2 + x-4 için f'(7) kaçtır? 2 Çözüm : 3 X+3 + lx)= () 3(1) +*2-4 13 f) x+ 5 3x+3 5 2 3 (433)

A60 b=2 2 i-b-1=1 b=2 20. Bir firma satış fiyatı 800 TL olan telefonlarından haftada A adet satabilmektedir. Telefonun satışında yapılan her 40 TL lik indirime karşılık haftalık satış adedi %25 oranında art- maktadır. Buna göre, firmanın telefonunun satışında haftalık kârı- nin en fazla olabilmesi için telefonun satış fiyatı kaç TL olmalıdır? A) 480 B B) 520 C) 560 D) 600 E) 720

9. Gerçek sayılardan gerçek sayılara tanımlı f(x) = x2 – 3x2 + mx + 2 - fonksiyonu bire bir ve örtendir. Buna göre, m’nin en geniş değer aralığı aşağıdakilerden hangisidir? A) (-0, 3] B) (-0, 2] C) [2, 4] D) (3, 6] E) [3,00)

24. Türevlenebilir f ve g fonksiyonları için, f(x) = x X g(x) g'(1) = -12 eşitlikleri veriliyor. f(1) = 1 f(x) fonksiyonunun x = 1 apsisli noktadaki tü- revi 1 olduğuna göre, g(1) değeri kaç olabilir? A) -4 B)-1 C) 1 D) 3 E) 4

6 MEB 2018 - 3. f: R → R ve g: R → Rolmak üzere 2-07 f(x) = 11 - 2x1 + 12x-1- x?l ve g(x) = x2 – 3x 12 fonksiyonları veriliyor. -ex + (xand2 Buna göre (fog)'(1) kaçtır? A) -12 B)-6 CO D) 8 q Göre ? #'(-2,4-444 f 1 E) 12

aritax Arax hafix (xo a f (d'all de a OM D APOIEMI 8. 6. Gerçel sayılar kümesinde tanımlı ve türevlenebilir bir f fonksiyonu her x gerçel sayısı için f'(2-x) - f'(x) = 0 eşitliğini sağlamaktadır. f(2) = 2.f(0) = 4 olduğuna göre, f(1) kaçtır? A) 16 B) 12 C) 6 D) 3 E) 2 6) D 5) D

Integral ve Uygulamaları 7. y=f(x) fonksiyonunun grafiğinin herhangi bir (x, y) noktasındaki teğetinin eğimi o noktanın apsisinin 4 katından 5 fazladır. f(-1)=5 olduğuna göre, f(2) kaçtır? E) 36 A) 26 B) 28 C) 30 D) 32 f'(2) = 10 1

Türev Alma Kuralları 2 1 1. La 4. f(2x + 1) = 2x2 + x + 1 fonksiyonu veriliyor. Buna göre, f(3) + f'(3) ifadesinin değeri kaçtır? 17 19 Dit 13 2 A) B) 15 2 C) E) 5 4X+1 2. f(x) = x² - 1 fonksiyonu veriliyor. VJUH IUN (fofl'?) değeri kaçtır?

4. y - y = x2 - mx-n parabolünün x eksenini kestiği noktalardan çizilen teğetler birbirine diktir. Buna göre, m ve n arasındaki bağıntı aşağıdakilerden hangisidir? - A) m2 + 4n = 1 B) mp-n=-1 C) m2 - 2n = 1 D) m2 - 2n = -1 E) m2 + 4n = -1 m m