Polinomlarla İşlemler Soruları

Lise Matematik
Polinomlarla İşlemlertr
P(x) polinomunun (x² - 2x - 3) ile bölümün-
den bölüm Q(x), kalan 3x + 1 dir.
Buna göre, P(x) polinomunun (x - 3) ile
bölümünden elde dilen bölüm ve kalanın
toplamı kaçtır?
A)(x-1). Q(x)
(x-1). Q(x) + 1
B) (x + 1). Q(x) + 3
D) (x + 1). Q(x)+13
E)(x-1). Q(x) + 3

Lise Matematik
Polinomlarla İşlemlerP(x) polinomunun (x² - 2x - 3) ile bölu
den bölüm Q(x), kalan 3x + 1 dir.
Buna göre, P(x) polinomunun (x - 3) ile
bölümünden elde dilen bölüm ve kalanın
toplamı kaçtır?
A) (x-1). Q(x)
) (x-1). Q(x) + 1
B) (x + 1) - Q(x) + 3
D) (x + 1). Q(x)+13
E(x-1) - Q(x) + 3

Lise Matematik
Polinomlarla İşlemlertT
P(x) polinomunun (x² - 2x - 3) ile bölümün-
den bölüm Q(x), kalan 3x + 1 dir.
Buna göre, P(x) polinomunun (x - 3) ile
bölümünden elde dilen bölüm ve kalanın
toplamı kaçtır?
A) (x-1) - Q(x)
2)(x-1) - Q(x) + 1
B) (x + 1). Q(x) + 3
D) (x + 1). Q(x)+13
E(x − 1) · Q(x) + 3

Lise Matematik
Polinomlarla İşlemlerD. k pozitif bir tam sayı olmak üzere,
P₁(x) = (x - 1) (x - 2)... (x - k)
polinomu tanımlanıyor.
Buna göre,
1. Pg(m) = 0 eşitliğini sağlayan 8 farklı m değeri vardır.
II. P-(6) = P6(7)
P5(7)
P₁(7)
4
P₁ (6)
4
P3 (6)
yargılarından hangileri doğrudur?
A) Yalnız I
B) I ve II
III.
D) II ve III
E) I, II ve III
C) I ve III

Lise Matematik
Polinomlarla İşlemler15. Bir polinomun katsayılarından oluşan sıralı n'liye poll-
nomun "katsayılar sıralısı" denir. Bu sıralılar yazılırken.
sabit terimden başlanarak artan derecelere göre sırala-
nir.
Örneğin,
•
.
x³+4x²-3x + 7 polinomunun katsayılar sıralısı
(7,-3, 4, 1) sıralı dörtlüsüdür.
x² + 7 polinomunun katsayılar sıralısı (7, 0, 1) sıralı
üçlüsüdür.
Katsayılar sıralısı (3, b, a, 1) olan bir polinomun, kat-
sayılar sıralısı (1, -1, 1) olan pollnoma tam bölündü-
ğü bilindiğine göre, b değerl kaçtır?
A)-2
B) -1
C) 0
D) 1
E) 2

Lise Matematik
Polinomlarla İşlemler51
E
R
B
A
K
A
N DI
18- P(x + 3) polinomunun sabit terimi, P(x - 2)
polinomunun katsayılar toplamına eşittir.
P(x + 2) = P(2x - 3) - P(x) + x²
eşitliğine göre P(x) polinomunun katsayılar
toplamı kaçtır?
A) 0
B) 1
P(-1)
C) 2
Pri) +
D) 3
1
E) 4
abileceği
U

Lise Matematik
Polinomlarla İşlemlerN 17- P(x-2) polinomunun sabit terimi 2
E
UMET -
C
Q(x + 3) polinomunun katsayılar toplamı - 1
olduğuna göre,
3.P(3 - 5x) + 4Q(5x - 1) polinomunun kat-
sayılar toplamı kaçtır?
A) 1
B) 2
C) 3 D) 4 E) 5
(+1
+2=
D)

Lise Matematik
Polinomlarla İşlemleral
siyonu
br²
E) 12
B
15. P(x) ve Q(x) gerçel katsayılı birer polinom olmak üzere,
• P(x) polinomu, grafiği y eksenine göre simetrik
olan ikinci dereceden bir polinomdur.
•
Q(x) polinomu, grafiği orijine göre simetrik olan
birinci dereceden bir polinomdur.
•
P(x) ve Q(x) polinomlarının katsayılar toplamı
birbirine eşittir.
• P(x) polinomunun (x - 2) ile bölümünden kalan
ile Q(x) polinomunun (x + 1) ile bölümünden
kalan birbirine eşittir.
bilgileri veriliyor.
Buna göre, P(x) polinomu aşağıdakilerden hangisi
olabilir?
A) x²-2x
C) 4x2-9
P(x) Gift dereceli
a(x)=Tek
P(4)= Q(4)
P(x) = ax²+bx+c
Q/N)= axtb
E) 2x²-5
B) 5x²-x-2
D) 2x² + 1
P/2) = Q(-4)
Atbtc
P(2)=49+2b ==9+b
7/71) = -9 +6

Lise Matematik
Polinomlarla İşlemlerav smlud
02.
CAP
P(x - 2) = x3 - 2x² + ax - 1
polinomu veriliyor.
0
P(x + 1) polinomunun katsayılar toplamı 11 old st
ğuna göre, P(x) polinomunun sabit terimi kaçtırma
2.
A) -11 B)-12 C) -13 D) -14 E) -15
P(2)=11
-17.
-1
E
19
pc
Q
ga
tir
A)

Lise Matematik
Polinomlarla İşlemlerTEST- 8
7.
Başkatsayısı 2 olan üçüncü dereceden bir P(x) polinomu
(x - 1), (x + 1) ve (x-3) ile tam bölünebilmektedir.
POLINOMLA
Buna göre, P(x) polinomunun x-2 ile bölümünden kalan
kaçtır?
A) -12
-6
C) 4
D) 8 E) 24

Lise Matematik
Polinomlarla İşlemler5. Bir polinomun katsayılarından oluşan sıralı n'liye poll-
nomun "katsayılar sıralısı" denir. Bu sıralılar yazılırken
sabit terimden başlanarak artan derecelere göre sırala-
nir.
Örneğin,
•
+³+4x²-3x + 7 polinomunun katsayılar sıralısı
(7,-3, 4, 1) sıralı dörtlüsüdür.
+7 polinomunun katsayılar sıralışı (7, 0, 1) sıralı
üçlüsüdür.
Katsayılar sıralısı (3, b, a, 1) olan bir polinomun, kat-
sayılar sıralısı (1, -1, 1) olan pollnoma tam bölündü-
ğü bilindiğine göre, b değerl kaçtır?
A) -2
B)-1
C) 0
D) 1
E) 2

Lise Matematik
Polinomlarla İşlemler10. x ve y birer tam sayı olmak üzere
-8≤x<5
-1 <y≤7
eşitsizlikleri veriliyor.
14
-24
XXL
A = 3x - 2y eşitliği için A'nın alabileceği en büyük ve en küçük
değerler sırasıyla Amax ve Amin ile gösteriliyor.
Buna göre Amax - Amin farkı kaçtır?
A) -50
B)-24
C) 24
D) 50
M-24≤ 3x < 15
11 6 -2 4 X 2
E) 59

Lise Matematik
Polinomlarla İşlemler4. m ve n birer pozitif tam sayı olmak üzere,
P(x) = (x + m).(x + n)
polinomunun katsayılarının toplamı 24 olduğu-
na göre, m + n toplamı aşağıdakilerden hangisi
olabilir?
A) 10 B) 8 C) 6 D) 4 E) 2
10. SINIF MATEMATİK VİDEO ANLATIM FASİKÜLLERİ
1
1
1
2P(x)
A) 2
Q(x³)
Yukarıda verilen şer
nomunun derecesi
B) 3
Polin

Lise Matematik
Polinomlarla İşlemler107
x+u ==
16=x+4
x = 12
sq
35b
53
n-n+1
2
23
=su
n²n=108
2131
16. n bir doğal sayı olmak üzere
polinomu veriliyor.
300T2
3+²+₁
8=8-x
108/2
542
27 3
93742
3
108
sy
endemik-
P(4)=54
P(x) = (x + 1) + (x + 2) + ... + (x + n)
(0(n+1)-(n+2
n²+3n+2= 108
P(x) polinomunun katsayılar toplamı 54 olduğuna
göre n kaçtır?
n²+37=106
AT6
B18
C) 9
D) 12
1=54
n(n+3)=106
E) 15
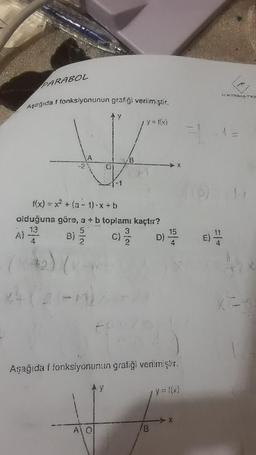
Lise Matematik
Polinomlarla İşlemlerPARABOL
Aşağıda f fonksiyonunun grafiği verilmiştir.
A)
f(x) = x² + (a-1).x+b
olduğuna göre, a + b toplamı kaçtır?
13
4
B)
(2) (
5/2
B
A O
y = f(x)
y
Aşağıda í fonksiyonunun grafiği verilmiştir.
3
C)/2 D) 1/5/20
4
B
y=f(x)
(p)
NATTIMATKE
E) 1/1/2

Lise Matematik
Polinomlarla İşlemler. P(x) polinomunun x + 3 ile bölümünden kalan -4,
bölüm A(x) dir. A(x) polinomunun x - 1 ile bölümün-
den kalan 2 dir. P(-3)=U
polinomunun x² + 2x - 3 ile bölü-
hangisidir?
Buna göre, P(x)
münden kalan aşağıdakilerden
A) 2x - 6
B) 2x + 2
stop snup D) -4x-6
C)-4x+8
E) 6x-3 ohilog (x)9
